
7. КОРРЕКЦИЯ НЕЛИНЕЙНЫХ СИСТЕМ
7.1. Линейная коррекция нелинейных систем
Рассмотрим задачу синтеза нелинейных систем как задачу введения в заданную систему дополнительных устройств (корректирующих) для удовлетворения предъявляемым к системе техническим требованиям.
Для достижения требуемой точности и качества процесса в нелинейные системы можно вводить линейные корректирующие устройства такие же, как и в линейных системах. Эти линейные корректирующие устройства могут быть последовательными (с введением производных, интегралов и т. п.) и параллельными (в виде местных обратных связей различного типа).
Рассмотрим системы с одной нечетно-симметричной однозначной нелинейностью F (x) , гармоническая линеаризация
которой имеет вид |
|
F (x) = q(a)x , |
(7.1) |
где коэффициент гармонической линеаризации принимает ограниченные значения
0 q qm или qн q qm . |
|
(7.2) |
Случаи наличия нелинейностей, когда коэффициент |
q(a) |
|
принимает бесконечное значение при |
a = 0 , здесь |
не |
рассматриваются, так как в этих случаях невозможно обеспечить устойчивое равновесное состояние системы в нулевой точке и установившийся режим будет автоколебательным. В этих случаях путем введения линейных корректирующих устройств можно добиваться приемлемых значений параметров (a, ω) автоколебаний.
Но это следует делать с помощью методов расчета автоколебаний. Здесь мы будем рассматривать точность и качество процессов около устойчивого равновесного состояния в нулевой точке.
Пусть схема системы имеет вид, изображенный на рис. 7.1. Положим, что линейное корректирующее устройство любого типа
вводится в одну из линейных частей, т. е. в блок W |
( p) |
или W |
2 |
( p) , не |
1 |
|
|
|
охватывая нелинейного звена F (x) .
163
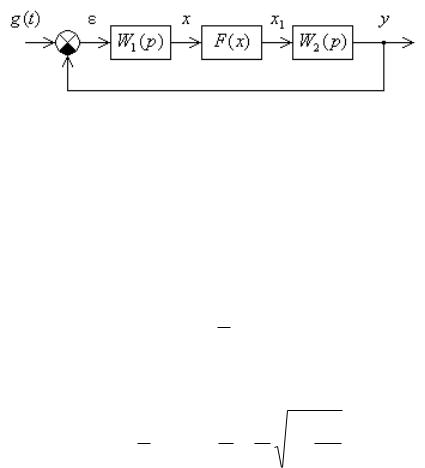
Рис. 7.1
Условимся в формуле записывать
q
(
гармонической линеаризации (7.1)
a) = kq0 (a) , |
(7.3) |
где k – коэффициент усиления. Тогда выражение
q |
(a) |
0 |
|
можно
получить в виде
Например, коэффициент q0
(
q0 (a) = 1k q(a) .
для характеристики с насыщением получаем a) :
|
|
|
2 |
|
|
|
q |
0 |
(a) = |
|
arcsin |
||
π |
|
|||||
|
|
|
||||
|
|
|
|
|||
|
|
|
|
|
|
b |
− |
b |
1 |
− |
|
A |
A |
||||
|
|
|
b |
2 |
|
|
|
|
A |
2 |
|
|
||
.
Указанный в формуле (7.3) коэффициент k будем относить к передаточной функции линейной части системы. Так, для схемы рис, 7.1 передаточную функцию такой приведенной линейной части будем записывать в виде
W |
( p) |
лп |
|
= kW |
( p) |
л |
|
=
kW ( p)W |
( |
|
1 |
2 |
|
p)
,
(7.4)
где k – коэффициент, выделенный из нелинейности согласно (7.3). Величину q0 (a) будем называть нормированным
коэффициентом гармонической линеаризации. Тогда синтез корректирующего устройства можно производить следующим образом.
1. Строится логарифмическая амплитудная частотная характеристика первоначально заданной приведенной линейной части системы:
Wлп ( p) = kW1( p)W2 ( p) ,
где k – коэффициент усиления, перенесенный из нелинейности.
2. Формируется желаемая логарифмическая амплитудная частотная характеристика линейной части Wж ( p) в соответствии с требованиями точности и качества процессов, как это изложено в
164
теории линейных систем.
3.Синтезируется линейное корректирующее устройство также методом линейной теории.
4.Вычерчивается логарифмическая фазовая частотная характеристика полученной скорректированной линейной части системы.
В дополнение ко всем этим операциям, выполняемым по линейной теории, добавляется еще один пункт, учитывающий
нелинейность
F (x)
в нормированном виде.
5. Для данной нелинейности с использованием нормированного
коэффициента q0 (a) |
строится «запретная» зона, соответствующая |
|||||
желаемому показателю колебательности |
M |
. Внутрь этой зоны не |
||||
|
|
|
|
|
|
|
должна |
заходить |
фазовая |
частотная |
характеристика |
||
скорректированной линейной части системы. Та кривая M = const , которой касается полученная фазовая характеристика, определяет значение показателя колебательности данной скорректированной системы. Если необходимо его уменьшить, то нужно несколько изменить параметры полученного выше линейного корректирующего устройства, следя за тем, чтобы не допускать существенного искажения желаемых свойств логарифмической амплитудной частотной характеристики приведенной линейной части, положенных первоначально в основу расчета.
Этот пятый пункт процедуры синтеза в совокупности с предыдущими обеспечивает нужные качества процессов в замкнутой нелинейной системе в целом. Следовательно, прежде чем приступать к синтезу линейного корректирующего устройства в нелинейной системе, необходимо научиться строить запретную зону по показателю колебательности при заданной нелинейности. Такое построение может производиться методом гармонической линеаризации, поскольку речь идет о колебательных переходных процессах.
Рассмотрим методику этого построения. Ограничиваясь рассмотрением однозначных нелинейностей (7.1) о ограниченными значениями коэффициента гармонической линеаризации (7.2) и используя его нормирование (7.3), получим следующее выражение для передаточной функции разомкнутой цепи гармонически линеаризованной системы:
W ( p, a) = kq0 (a)Wл ( p) = q0 (a)Wлп ( p).
165
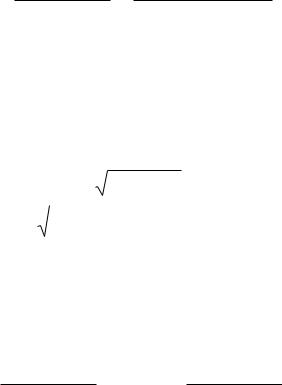
Передаточная функция замкнутой системы примет вид
|
W ( p, a) |
|
q |
(a)W |
лп |
( p) |
|
|||
Ф( p, a) = |
|
= |
0 |
|
|
|
|
. |
||
+W ( p, a) |
+ q |
(a)W |
|
|
( p) |
|||||
1 |
1 |
лп |
|
|||||||
|
|
|
|
0 |
|
|
|
|
||
Выделим вещественные и мнимые части после замены обозначив их следующим образом:
Wлп ( jω) =U (ω) + jV (ω).
Тогда для показателя колебательности |
M =| Ф( jω, a) |max |
p = jω ,
имеем
выражение
Отсюда после равных значений M
|
|
q0 U 2 +V 2 |
|||
M = |
|
|
|
|
. |
|
|
|
|
||
(1 + q U )2 |
+ (q V )2 |
||||
|
|
0 |
0 |
|
|
преобразования |
получаем |
||||
на комплексной плоскости (U
уравнение линий , V ) в виде
|
(U −U |
0 |
) |
|||
|
|
|
|
|
||
где |
|
|
|
|
|
|
R = − |
M |
|
|
|
||
|
2 |
|
|
|
||
q |
(M |
−1) |
||||
|
||||||
0 |
|
|
|
|
|
|
При определенном значении
2 |
+V |
2 |
2 |
, |
|
|
|
|
= R |
|
|||
, |
|
U |
|
= − |
|
M |
|
0 |
|
|
|||
|
|
|
q |
(M |
||
|
|
|
|
|||
|
|
|
|
|
0 |
|
q0 |
линии M = |
|||||
2 |
|
|
2 |
−1) |
. |
|
||
|
|
|
const |
|
|
(7.5)
(7.6)
получают вид
окружностей. Но согласно (7.2) и (7.3) величина |
q0 |
любое значение в интервале |
|
0 q0 q0m или q0н q q0m , |
|
может принимать
(7.7)
где числа
q0н
и |
q0m |
получают свои определенные значения для
каждой конкретной нелинейности. В соответствии с этим, согласно
(7.6), координата центра окружности |
U0 |
и радиус |
R |
будут тоже |
|
|
|
|
меняться в определенных для каждой нелинейности пределах. Следовательно, каждая линия M = const будет определяться как огибающая непрерывного множества постепенно меняющихся окружностей. При этом в случае первого неравенства (7.7) линия M = const будет незамкнутой (рис. 7.2, а), так как в начальной точке q0 = 0 из (7.6) имеем U0 = , R = .
166
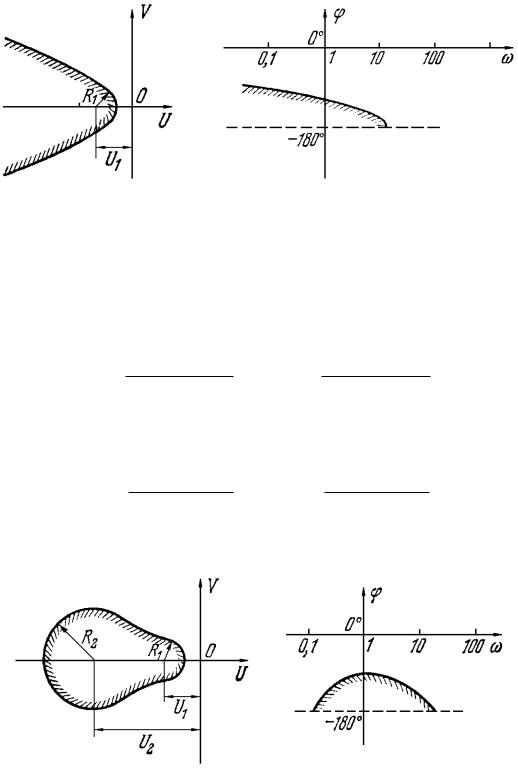
а |
б |
Рис. 7.2
Показанные на рис. 7.2, а величины |
1 |
и |
U |
1 |
согласно |
|
R |
|
|
|
определяются выражениями
R |
= |
|
M |
|
, |
U |
|
|
|
|
1 |
||||
1 |
q |
|
(M |
2 |
−1) |
|
|
|
|
|
|
||||
|
0m |
|
|
|
|||
|
|
|
|
|
|
|
В случае второго неравенства замкнутой (рис. 7.3, а), причем
|
|
M |
2 |
|
= − |
|
|
|
|
|
|
2 |
|
|
q |
|
(M |
− |
|
0m |
|
|||
|
|
|
|
(7.7) линия
.
1)
M = const
|
|
M |
|
|
|
|
|
M |
2 |
|
R2 = |
|
|
|
, |
U 2 = − |
|
|
, |
||
|
|
2 |
|
|
|
2 |
||||
q |
|
(M |
−1) |
|
q |
|
(M |
−1) |
||
0н |
|
|
0н |
|
||||||
|
|
|
|
|
|
|
|
|
а значения U |
1 |
и R |
прежние. |
|
1 |
|
(7.6),
(7.8)
будет
(7.9)
а |
б |
|
Рис 7.3 |
Поскольку синтез линейного корректирующего устройства проводится по логарифмическим частотным характеристикам, то изображенные на рис. 7.2, а и рис. 7.3, а линии M = const (запретные
167
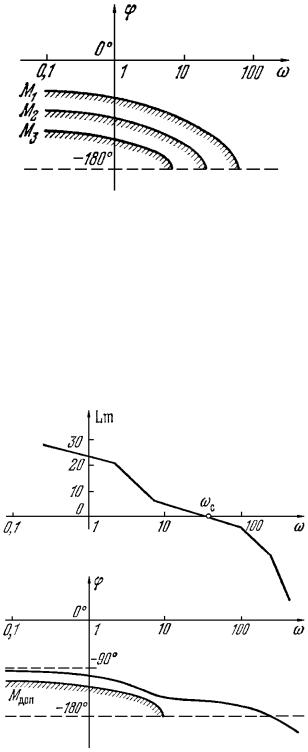
зоны) должны быть перенесены в систему координат логарифмических характеристик. Это показано соответственно на рис. 7.2, б и рис. 7.3, б.
Взяв разные постоянные значения M = M1, M 2 , , получим
серию кривых
M = const
(рис. 7.4).
Рис. 7.4
Логарифмические частотные характеристики скорректированной по изложенной выше процедуре системы должны быть такими, чтобы фазовая характеристика линейной части (ω) не
заходила внутрь запретной зоны, значением показателя колебательности
определяемой допустимым
M |
(рис. 7.5). |
|
Рис. 7.5
168
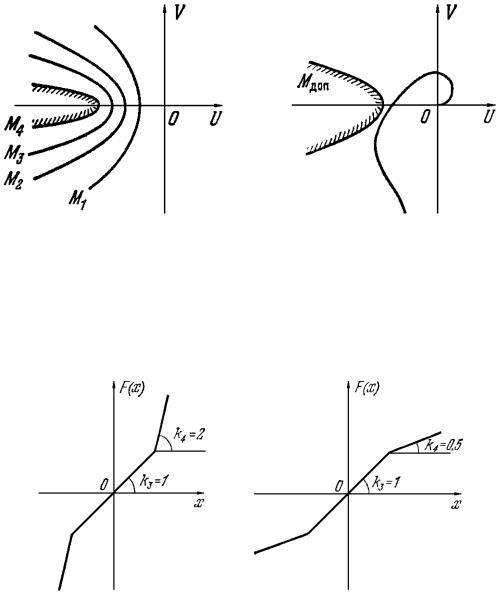
Если расчет корректирующего устройства ведется по амплитудно-фазовым частотным характеристикам, то на поле координат (U , V ) получается серия кривых M = const (рис. 7.6, а), причем амплитудно-фазовая частотная характеристика приведенной линейной части скорректированной системы не должна заходить внутрь запретной зоны, определяемой здесь допустимым значением показателя колебательности M (рис. 7.6, б).
а |
б |
Рис. 7.6
Пример.
нелинейности
7.1.
F (x)
Пусть имеется два варианта (рис. |
7.7, а и б) |
в системе, изображенной на рис. 7.1. |
|
а |
б |
Рис. 7.7
Передаточные функции линейных звеньев (рис. 7.1) заданы в
виде
169

|
|
|
|
|
k |
|
|
|
|
|
|
k |
|
|
|
|
|
|
W1 |
( p) = |
1 |
, |
W2 ( p) = |
|
|
|
1 |
. |
|
|
|||
|
|
|
|
T |
|
|
|
|
|
|||||||
|
|
|
|
T p +1 |
|
|
|
p +1 |
|
|
||||||
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wл ( p) = |
|
|
|
kл |
|
, |
kл = k1k2 . |
|
|
|||||
|
|
(T1 p |
|
|
|
|
|
|||||||||
|
|
|
|
+1)(T2 p +1) |
|
|
|
|
|
|
|
|||||
|
Заданы T |
= 0,01, T = 0,04 , а величину k |
л |
можно изменять. |
||||||||||||
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение. Крутизна наклона линейных отрезков нелинейной |
|||||||||||||||
характеристики |
определяется коэффициентами |
k3 и |
k4 |
причем в |
||||||||||||
первом случае (рис. 7.7, а) |
k3 |
=1, k4 = 2 , а во втором случае (рис. 7.7, |
||||||||||||||
б) |
k3 =1, k4 = 0,5 . |
Здесь |
|
нелинейность |
|
|
представлена |
уже в |
||||||||
нормированном |
виде, поскольку |
k3 =1. Поэтому тут |
q(a) = q0 (a) . |
|||||||||||||
Очевидно, что коэффициент q(a) меняется в пределах между k3 т. е. в первом и втором случаях соответственно имеем 1 q0
и k4
2 |
; |
0,5 q
1
.
Линия
M = const
будет иметь вид, представленный на
рис. 7.3, где, согласно (7.8) и (7.9), для первого случая (рис. 7.7, а)
|
|
M |
|
|
M 2 |
||
R1 |
= |
|
, U1 |
= − |
|
|
, |
2(M 2 −1) |
2(M 2 |
|
|||||
|
|
|
|
−1) |
|||
R |
= |
M |
, |
|
|
|
|||
2 |
M |
2 |
−1 |
|
|
|
|||
|
|
|
||
а для второго (рис. 7.7, б)
|
|
R = |
|
|
M |
, |
|
|
|
|
|
|
|
||
|
|
1 |
M |
2 |
−1 |
|
|
|
|
|
|
||||
|
|
|
|
|
|||
R |
= |
|
M |
|
|
, |
|
|
|
|
|
|
|||
2 |
|
0,5(M |
2 |
−1) |
|
||
|
|
|
|||||
|
|
|
|
|
|||
U2
U1 U 2
|
M |
2 |
|
|
|
= − |
|
, |
|
||
|
2 |
|
|
||
|
M |
−1 |
|
||
|
|
|
|||
|
M |
2 |
|
|
|
= − |
|
, |
|
||
|
2 |
|
|
||
|
M |
−1 |
|
|
|
|
|
|
|
||
|
|
|
M |
2 |
|
= − |
|
|
|
||
|
|
2 |
|
||
|
0,5(M |
−1) |
|||
|
|
||||
Придавая М разные значения, получаем кривые, показанные на рис. 7.8, а и б соответственно для первого и второго случаев. Там же нанесены амплитудно-фазовые характеристики линейной части для трех разных значений kл .
170
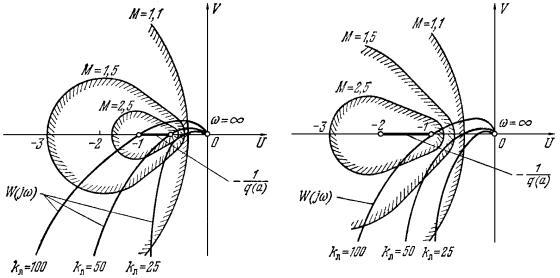
а |
б |
Рис. 7.8
Из этих графиков видно, что по сравнению с чисто линейной системой в первом случае (рис. 7.8, а) за счет нелинейности запретная зона выпучивается вправо, а во втором (рис. 7.8, б) – влево. Следовательно, в первом случае за счет нелинейности повышается колебательность системы, а во втором – нет. Интересно также отметить то, что автоколебания в нелинейной системе определяются условием
Wл ( j ) = −1/ q(a) .
Правая часть этого равенства изображается графически отрезками вещественной оси соответственно для первого и второго случаев: −1 U 0,5, − 2 q0 −1. Линейная же система устойчива,
если кривая W ( jω) пересекает вещественную ось правее точки −1.
Следовательно, во втором случае область устойчивости нелинейной системы сохраняется, как в линейной системе, а автоколебания возникают уже за ее пределами. В первом же случае область устойчивости системы за счет нелинейности сужается, и автоколебания возникают там, где линейная система была бы устойчива.
171
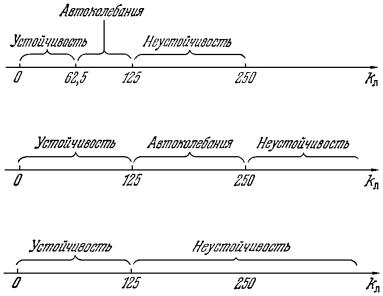
а
б
в
Рис. 7.9
На рис. 7.9 это показано графически: а) для первого случая, б) для второго случая, в) для чисто линейной системы.
7.2. Нелинейные корректирующие устройства
Специального вида нелинейности можно вводить в линейную систему в качестве корректирующих устройств; в результате этого в скорректированном виде линейная система становится нелинейной. Коррекцию с помощью нелинейных устройств производят также и в нелинейных системах. Нелинейная коррекция обладает более широкими возможностями, чем линейная, так как она, во-первых, дает большее разнообразие форм частотных характеристик и, вовторых, она позволяет менять форму частотных характеристик в зависимости от величины амплитуды сигнала. Последнее свойство нелинейной коррекции является принципиально новым качеством по сравнению с линейной коррекцией. Оно придает системе как бы свойство самонастройки по величине ошибки, возникающей в системе в процессе управления.
На рис. 7.10 в качестве примера показана структурная схема нелинейного динамического корректирующего звена, состоящего из двух линейных корректирующих звеньев 1 и 3 и нелинейного звена с насыщением 2. При T1 T2 звено 1 является пропорционально-
дифференцирующим звеном, т. е. фильтром верхних частот, а звено 3
172
