
6.УСТОЙЧИВОСТЬ НЕЛИНЕЙНЫХ СИСТЕМ
6.1.Основные понятия по Ляпунову об устойчивости
нелинейных систем
Общим методом точного исследования динамики, в том числе и устойчивости, нелинейных систем является метод фазовых траекторий. Однако область его применения практически ограничена системами второго порядка.
Очевидно, мощным средством исследования нелинейных систем автоматического управления являются вычислительные машины.
Трудности точного исследования нелинейных систем привели к разработке, во-первых, методов, дающих достаточные критерии устойчивости, т. е. критерии, позволяющие определить часть полной области устойчивости системы, и, во-вторых, приближенных методов исследования. В первом случае нам заранее известен знак погрешности в определении предела устойчивости – предел всегда будет занижен, т. е. погрешность идет в запас устойчивости. Однако величина этой погрешности неизвестна и может быть сколь угодно большой. Во втором случае знак погрешности неизвестен, но зато часто имеется возможность как-то оценить сверху абсолютную величину погрешности.
Основоположником теории устойчивости нелинейных систем был А. М. Ляпунов, который в 1892 г. поставил общую задачу об устойчивости движения и сформулировал понятия устойчивости как для линеаризованных систем, так для существенно нелинейных систем. Дальнейшее развитие теория устойчивости нелинейных систем получила в работах И. Г. Четаева, А. И. Лурье, В. М. Попова, Р. Калмана, В. А. Якубовича и др.
В зависимости от наличия внешних воздействий на систему все системы управления могут быть разделены на автономные и неавтономные. В автономных системах внешние воздействия отсутствуют. К автономной системе может быть сведена любая из непрерывных систем при не зависящем от времени внешнем воздействии. В неавтономных системах существуют зависящие от времени внешние воздействия.
Так как в автономных нелинейных системах наиболее характерными: являются два процесса – равновесие и автоколебания,
138

то для них рассматриваются два различных понятия устойчивости: устойчивость равновесия и устойчивость автоколебаний. Для неавтономных систем существует понятие устойчивости процесса, обусловленного внешним воздействием.
Стремление применить для анализа нелинейных систем методы, аналогичные методам исследования линейных систем привело к введению понятий невозмущенных и возмущенных движений системы. Первое из этих понятий соответствует некоторому частному решению, а второе – совокупности иных возможных (общих) решений.
Под невозмущенным движением системы понимают одно из возможных расчетных движений системы при некоторых определенных начальных условиях и заданном внешнем воздействии. Всякое другое движение называется возмущенным. Можно считать, что любое возмущенное движение получается за счет приложения к системе кратковременного внешнего возмущения при t = 0 .
Состояние равновесия и установившийся режим автоколебаний можно рассматривать как важные частные случаи невозмущенных движений автономной системы.
Будем рассматривать движение непрерывной системы в фазовом пространстве вектора x = {x1, x2 , , xk , , xn}.
Невозмущенное движение выражается векторной функцией
x |
н |
(t) |
|
или совокупностью
n
функций
x |
н |
(t) |
|
k |
|||
|
|
. Любое возмущенное
движение описывается векторной функцией
x(t)
или совокупностью
n функций |
xk (t) . Вариация процесса описывается вектором |
|||||||
|
η(t) = x(t) − x |
н |
(t) |
|||||
|
|
|||||||
или совокупностью n функций |
|
|
|
|
|
|||
|
η |
|
(t) = x |
|
(t) − x |
н |
(t) |
|
|
k |
k |
k |
|||||
|
|
|
|
|
|
|||
(6.1)
(6.2)
и выражает различие невозмущенного и возмущенного движений. Для общего суждения об устойчивости движения пользуются
понятием устойчивости, данным А. М. Ляпуновым: движение
устойчиво, если для любой сколь угодно малой заданной области ε 
допустимых отклонений |
ηk |
от точки |
ηk = 0 |
можно указать |
область начальных значений
δ(ε)
, |
лежащую внутри области ε |
и обладающую тем свойством, что ни одно возмущенное движение,
139
начавшееся внутри области области ε .
δ
никогда не достигнет границы
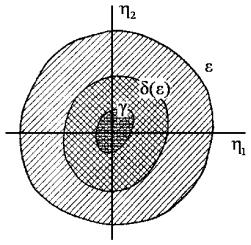
Рис. 6.1
Области |
ε |
и |
δ |
на плоскости |
η1 |
и |
η2 |
схематически показаны на |
рис. 6.1 |
|
|
|
|
|
Для характеристики устойчивости кроме областей |
ε |
и δ |
удобно |
||
ввести понятие области |
γ |
установившихся значений разности |
|||
возмущенного и невозмущенного движений. При t → |
|
|
|
||
|
|
η γ. |
|
|
(6.3) |
Вид области
γ
зависит от области начальных отклонений.
Нужно отметить два γ . В первом случае
практически важных частных случая областей
= 0 |
, т. е. |
|
|
lim k (t) = 0 . |
(6.4) |
|
t → |
|
Такое движение называют асимптотически устойчивым. Если для выполнения равенства (6.4) требуется, чтобы область начальных отклонений была достаточно мала, то говорят об асимптотической устойчивости в малом. Если эта область может иметь конечные размеры, то говорят об асимптотической устойчивости в большом. Если, наконец, равенство (6.4) выполняется при сколь угодно больших начальных отклонениях, то говорят об асимптотической
устойчивости в целом. |
|
|
|
Во втором частном случае область |
γ |
представляет собой |
|
отрезок на оси |
1 . В этом случае равенство (6.4) не выполняется при |
||
|
η |
|
|
сколь угодно малых отклонениях от равновесия и устойчивость относится к неасимптотической.
140
Все приведенные выше определения устойчивости могут быть отнесены к устойчивости состояния равновесия, автоколебаний и вынужденных процессов.
Для суждения об устойчивости автоколебаний вводится понятие
орбитальной устойчивости. |
|
|
|
|
|
Периодическое |
движение |
(автоколебание) в |
|
пространстве |
|
состояний изображается некоторой замкнутой кривой |
|
. Представляя |
|||
|
|||||
любую траекторию геометрическим местом конца |
|
вектора |
x(t) , |
||
можно для любого |
момента |
времени t определить кратчайшее |
|||
расстояние ох конца вектора |
x(t) |
до кривой , которое обозначим |
ρ[x(t),
]
.
Под орбитально асимптотически устойчивым периодическим движением в автономной системе (автоколебанием) будем понимать такое движение, для которого
lim ρ[x(t), t →
] =
0
.
(6.5)
Это условие можно выразить с помощью понятия невозмущенного движения, если учесть возможный сдвиг по времени
τ
между xн (t) и x(t) . Обозначив
η |
k |
(t, τ) = |
|
|
x |
|
(t) − x |
н |
(t |
|
k |
k |
||||
|
|
|
−
τ)
,
(6.6)
можно условие орбитальной асимптотической устойчивости сформулировать следующим образом: существуют такие
положительные вещественные значения |
τ = τ0 |
, для которых |
lim ηk (t, ) = 0. |
(6.7) |
|
t → |
|
|
Невыполнение условия (6.5) или (6.7) приводит к нарушению орбитальной асимптотической устойчивости.
Рассмотрим, как приведенные определения согласуются с изученными ранее явлениями в линейных системах автоматического управления.
Уравнения в вариациях для этих систем получаются линейными и однородными. Поэтому движения в линейных системах, у которых все корни характеристического уравнения имеют отрицательные действительные части, асимптотически устойчивы в целом. Если хотя бы один корень характеристического уравнения имеет положительную действительную часть, то любое движение в системе неустойчиво. Если один корень равен нулю (система нейтральна), то
141
движения в системе устойчивы по Ляпунову, но не асимптотически.
Областью притяжения |
γ |
в этом случае является отрезок оси |
1 |
. Если |
|
|
|
η |
|
имеется пара мнимых |
|
корней, то γ представляет собой |
область, |
|
внутри которой располагается замкнутая фазовая траектория
η(t)
,
соответствующая установившемуся
рассогласованию, к которому стремится |
η(t) |
при
t
периодическому
→ .
Рассмотрим некоторые примеры автономных и неавтономных систем и дадим характеристику устойчивости происходящих в этих системах процессов.
Пример. 6.1. Составить суждение об устойчивости по Ляпунову точки равновесия типа центр линейной консервативной системы второго порядка и найти области δ и γ для области ε , задаваемой
неравенствами
− a
x1
2a
,
− 2a x2
2a
,
где a – произвольное число.
Решение. Рассматривая фазовые траектории для этого случая можно убедиться, что если радиус-вектор точки, соответствующей начальным условиям не выходит за пределы окружности с центром в начале координат, лежащей внутри области ε , то движение никогда не достигает границы этой области ε . Движение будет совершаться по этой окружности сколь угодно долго.
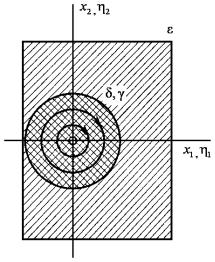
Таким образом, область δ совпадает с областью γ . Равновесие
устойчиво по Ляпунову, но не асимптотически. Области рассматриваемого случая показаны на рис. 6.2.
ε
,
δ
и
γ
для
Рис. 6.2
142
Пример
простейшей, гистерезисом
6.2. Рассмотреть релейной следящей при внешнем сигнале
устойчивость процессов |
в |
системе первого порядка |
с |
v(t) = At . Структурная схема |
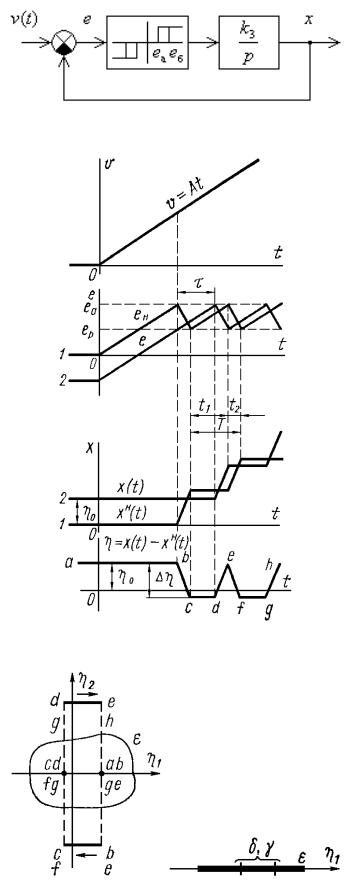
|
системы показана на рис. 6.3, а. Система состояния x .
Решение. На рис. 6.3, б построены
имеет одну координату
e(t) |
и |
x(t) |
для двух |
различных начальных условий: 1) – когда
x(0) = 0
и 2) – когда
x(0) = η0 . Первый из этих случаев принимается в качестве
невозмущенного, а второй – в качестве возмущенного движения.
Оба эти процесса приводят к колебаниям с одинаковыми периодами. Так как колебания происходят в неавтономной системе и зависят от внешнего воздействия v(t) , то они не могут быть названы
автоколебаниями. Период колебаний
T = t1 + t2 |
. Здесь |
t1 = (ea |
слагается
− e |
) / A |
b |
|
из двух |
отрезков |
– время, в |
течение |
времени: которого
внешний сигнал изменяется на величину ширины петли гистерезиса,
a |
t2 = (ea − eb ) /(k − A) |
– время, в течение которого при |
k A |
следящая система отрабатывает это рассогласование при условии продолжающегося увеличения внешнего сигнала. Отставание возмущенного процесса от невозмущенного τ = 0 / A зависит от
начальных условий возмущенного процесса. Для суждения об устойчивости рассматриваемого процесса определим вариацию
η(t) =
x(t) −
x |
н |
(t) |
|
. Эта зависимость
построена на рис. 6.3, б. По
истечении |
|
времени |
ta = (η0 − ea ) / A |
процесс |
становится |
|
периодическим с периодом T = t1 + t2 = k(ea − eb ) / A(k − A) . |
|
|||||
Диапазон изменения |
η(t) зависит от начального условия |
η0 : |
||||
η kτ = kη |
0 |
/ A |
|
|
|
|
|
|
|
|
|
|
|
и не может превышать величину kt2 = k(ea − eb ) / A(k − A) .
На рис. 6.3, в построен фазовый портрет процесса η(t) в координатах η1 = η и η2 = dη / dt .
143
а
б
в |
г |
Рис. 6.3
144
Координата
η2
изменяется не непрерывно и фазовая траектория
носит разрывной характер. Обозначив на кривой
η(t)
точки a, b, с, d,
e, f, g, h для различных моментов времени можно нанести соответствующие точки на фазовом портрете. Процесс перемещения изображающей точки на фазовой плоскости можно описать
следующим образом; неподвижность в точке |
ab , скачок |
b → b , |
равномерное движение по линии |
bc , скачок |
c → c , неподвижность в |
точке cd , скачок d → d , равномерное движение de e, скачок e → e , непрерывное движение ef и т. д.
Движение слагается из интервалов покоя, равномерного движения и скачков, а завершается разрывным предельным циклом
шириной |
Δη . Так как рассматриваемая система описывается |
дифференциальным уравнением первого порядка ( n = 1), то для |
|
суждения о ее устойчивости необходимо пользоваться не фазовой
плоскостью, а фазовой прямой с одной координатой η1 . |
|
|
На этой прямой (рис. 6.3, г) при заданном участке |
ε |
всегда |
можно выделить участок δ , необходимый для суждения об устойчивости по Ляпунову (неасимптотической). Для рассматриваемого примера этот участок совпадает с участком γ , в
пределах которого происходят колебания в системе. Попытка
обозначить область |
ε |
и искать область |
δ |
на фазовой плоскости для |
рассматриваемого примера рис. 6.3, в не может дать ответа об
устойчивости |
|
системы по Ляпунову, так как вторая фазовая |
|
координата |
η |
2 |
не соответствует порядку уравнения и для суждения |
|
|||
об устойчивости является излишней.
Ляпунов разработал два общих метода исследования устойчивости нелинейных систем.
Первый метод применим только для исследования устойчивости в малом линеаризуемых систем. Ляпунов при этом впервые доказал допустимость суждения об устойчивости в малом нелинейной системы по устойчивости линейной системы, полученной путем линеаризации исходной нелинейной системы. Далее, он доказал также, что в критических случаях, когда линеаризованная система находится на границе устойчивости, об устойчивости исходной нелинейной системы ничего нельзя сказать: она может быть
145

устойчива или неустойчива в зависимости от конкретного вида нелинейностей.
Второй метод Ляпунова, называемый прямым методом, является наиболее общим методом исследования устойчивости любых нелинейных систем. Он дает достаточные условия устойчивости, т. е. определяет часть области устойчивости.
6.2. Прямой метод Ляпунова
А. М. Ляпуновым предложен метод, позволяющий получать достаточные условия устойчивости нелинейных систем автоматического управления, получивший название прямого (или второго) метода Ляпунова.
Далее этот метод будет рассмотрен применительно к анализу устойчивости равновесия.
Рассмотрим автономную нелинейную систему, движение которой описывается системой нелинейных дифференциальных уравнений первого порядка в нормальной форме:
|
dx1 |
|
|
= (x , x |
2 |
,..., x |
n |
); |
|
|
|||||
|
|
|
|
||||||||||||
|
dt |
1 |
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 2 |
(x1, x2 |
,..., xn ); |
|
|
||||||||
|
|
|
|
|
(6.8) |
||||||||||
|
dt |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
.................................. |
|
|
|
|
|||||||||||
|
dxn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= (x , x |
2 |
,..., x |
n |
); |
|
|
||||||
|
|
|
|
|
|
||||||||||
|
dt |
|
|
n |
1 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или в более краткой записи
dx |
= (x |
, x |
|
,..., x |
|
), |
i =1, 2, , n |
|
i |
2 |
n |
||||||
dt |
i |
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Здесь x1, x2 , , xn – переменные, описывающие
(6.9)
состояние
системы, a
Ψi
– известные функции, заданные в пространстве этих
переменных.
Положение равновесия определяется системой уравнений
|
i (x1, x2 ,..., xn ) = 0, |
i =1, 2, , n . |
(6.10) |
||
Будем считать далее для простоты, что система уравнений (6.10) |
|||||
имеет |
единственное |
решение |
в |
начале |
координат |
x1 = 0, x2 = 0, , xn = 0 . |
|
|
|
|
|
146
Согласно прямому специальная функция V
(
методу Ляпунова в рассмотрение вводится x1, x2 , , xn ) (функция Ляпунова), заданная
впространстве состояний и обладающая следующими свойствами:
1.Эта функция непрерывна вместе со всеми своими частными производными первого порядка в некоторой открытой области, содержащей начало координат.
2. В начале координат функция
V (x |
, x |
2 |
, , x |
n |
) |
1 |
|
|
|
принимает
нулевое значение.
3. Всюду внутри функция V (x1, x2 , , xn
)
этой области, кроме начала координат, отлична от нуля и имеет значения одного и
того же знака. Такие функции называют знакоопределенными. Кроме того, существует еще понятие знакопостоянной функции, которая может принимать в области нулевые значения не только в начале координат, в остальных же точках она сохраняет постоянство знака.
А. М. Ляпуновым доказана справедливость следующего утверждения: если дифференциальные уравнения (6.9) движения таковы, что можно, найти знакоопределенную функцию V (x1, x2 , , xn ) , производная которой dV / dt в силу этих уравнений
была бы или знакопостоянной функцией противоположного знака с
V , или тождественно равной нулю, то равновесие системы в начале |
|||
координат устойчиво. |
|
|
|
Если производная |
dV / dt |
– знакоопределенная |
функция |
противоположного знака |
V , то равновесие системы в начале |
||
координат асимптотически устойчиво. |
|
||
Устойчивость (или асимптотическая устойчивость) |
положения |
||
равновесия при выполнении условий теоремы Ляпунова связана с
тем, обстоятельством, что для |
V -функции, обладающей |
перечисленными выше свойствами; можно построить в некоторой |
|
окрестности начала |
координат семейство замкнутых поверхностей |
равных значений V , |
описываемых уравнением |
V (x1, x2 , , xn ) = C |
(6.11) |
и заключающих начало координат внутри себя. При этом по мере, уменьшения C эти поверхности стягиваются к началу координат
(рис. 6.4).
147
