
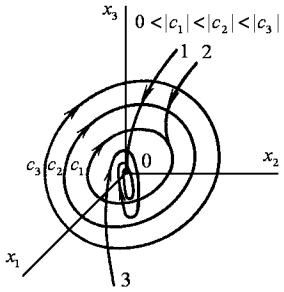
Рис. 6.4
На рис. 6.4 показано три типа траекторий движения: на
траектории 1 |
производная |
dV / dt |
знакоопределенна и имеет |
|
противоположный с V знак. Если все траектории относятся к типу 1, |
||||
то положение равновесия асимптотически устойчиво. |
||||
Траектория 2 соответствует случаю знакопостоянства |
||||
производной |
dV / dt |
и, следовательно, случаю устойчивости по |
||
Ляпунову (но не асимптотической устойчивости). При этом траектории могут «застревать» в тех точках пространства состояний, где производная dV / dt обращается в нуль, или даже замыкаться на поверхности V = C (рис. 6.4). При этом надлежащим подбором начальной точки всегда можно добиться того, что предельная точка или траектория размещалась в заданной окрестности положения равновесия.
Траектория 3 соответствует асимптотической устойчивости положения равновесия, хотя вдоль нее условия теоремы Ляпунова не выполняются. Возможность существования движения такого типа свидетельствует о том, что выполнение условий теоремы Ляпунова не является необходимым для устойчивости систем автоматического управления.
Теорема Ляпунова относится к устойчивости положения равновесия в малом, однако если удается подобрать V -функцию, поверхности равных значений которой включают в себя начало координат и имеют возрастающие по модулю по мере удаления от начала координат значения C , причем эти поверхности существуют в
148

некоторой конечной области, то можно сделать вывод об асимптотической устойчивости, в большом в пределах этой области,
если |
dV / dt |
в ней знакоопределена и имеет обратный знак с V . Если |
эти условия выполняются во всем фазовом пространстве, то положение равновесия асимптотически устойчиво в целом. Как и в случае устойчивости в малом, условия, при которых такие V - функции Ляпунова существуют, являются достаточными условиями устойчивости.
Если можно удовлетвориться суждением об устойчивости
положения равновесия системы в малом, искать |
V -функции не |
нужно. В этом случае вместо нелинейной системы можно исследовать устойчивость ее линейного приближения, получающегося путем линеаризации за счет разложения в точке равновесия нелинейных зависимостей в степенные ряды и отбрасывания членов со степенями выше первой.
При этом справедливы следующие теоремы Ляпунова о линейном приближении (первый метод Ляпунова):
1. если вещественные части всех корней характеристического уравнения, составленного для уравнений линейного приближения
dx |
|
x |
+ + a |
x |
|
(i =1, , n) |
i = a |
n |
|||||
dt |
i1 |
1 |
in |
|
|
|
|
|
|
|
|
|
|
отрицательны, то положение равновесия в исходной нелинейной системе асимптотически устойчиво в малом;
2. если среди корней характеристического уравнения имеется хотя бы один, имеющий положительную часть, то положение равновесия неустойчиво.
Эти теоремы являются основными для применения критериев устойчивости линейных систем при анализе устойчивости в малом нелинейных систем.
Если V -функция Ляпунова подобрана, то для определения знака ее производной нет надобности решать уравнения движения системы (6.9). Действительно, поскольку
|
|
dV (x , x |
2 |
, , x |
n |
) |
n |
V (x , x |
|
|
, , x |
|
) |
|
dx |
||||||||||
|
|
|
|
1 |
|
|
|
|
= |
|
|
1 |
2 |
|
|
|
n |
|
|
i |
, |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi |
|
|
|
|
|
||||||
|
|
|
|
dt |
|
|
|
|
i =1 |
|
|
|
|
|
|
|
dt |
||||||||
то на основании (18.9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
dV (x , x |
2 |
, , x |
n |
) |
n |
V (x , x |
|
, , x |
|
|
) |
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
= |
|
1 |
|
2 |
|
|
n |
|
i |
(x1, x2 ,..., xn ) . |
||||||||||
|
|
dt |
|
|
|
|
|
|
xi |
|
|
|
|
||||||||||||
|
|
|
|
|
|
i =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
149
Большие трудности представляет подбор |
V -функций при |
практическом использовании прямого метода Ляпунова. К сожалению, здесь нет однозначных способов построения этих функций и приходится в значительной степени полагаться на интуицию. Это обстоятельство ограничивает практическое применение прямого метода Ляпунова. Он чаще используется в доказательствах теорем об устойчивости определенных классов нелинейных систем и значительно реже для исследования устойчивости конкретных систем.
а
б
Рис. 6.5
Для систем автоматического управления, имеющих структуру, показанную на рис. 6.5, а, с характеристикой нелинейного звена,
удовлетворяющей условиям e z(e) 0; z(0) = 0 (рис. 6.5, б), |
V - |
функции могут быть взяты в форме, предложенной А.И. Лурье и В.Н. Постниковым:
e |
|
V (x1, x2 ,..., xn ) = L(x1, x2 ,..., xn ) + β z(ξ)dξ , |
(6.12) |
0 |
|
где L(x1, x2 , , xn ) – квадратичная форма координат
150

αij
и
β
n n
L(x1, x2 , , xn ) = αij xi x j ; i =1 j =1
– постоянные коэффициенты, причем αij = α
ji
.
(6.13)
В выражении (6.12) второе слагаемое заведомо знакоопределенно, а знакоопределенность того же типа для первого слагаемого может быть обеспечена надлежащим выбором коэффициентов αij .
Можно показать, что поверхности равных значений функций Ляпунова, взятых в такой форме, содержат внутри себя начало координат и имеют значения C , возрастающие по модулю по мере удаления от начала координат. Эти поверхности заполняют собой все пространство и могут при соответствующем выборе коэффициентов α и β служить для суждения об устойчивости равновесия системы в
целом.
С помощью V -функций такого типа удается решить некоторые практические задачи, связанные с анализом устойчивости нелинейных систем автоматического управления.
Пример 6.3. Проверить устойчивость равновесия в системе (рис. 6.5, а), содержащей в линейной части инерционное звено
|
|
|
Wл ( p) = |
|
|
|
k |
|
. |
|
(6.14) |
|||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
1 + pT |
|
|
|||||
Решение. Уравнения движения системы могут быть записаны в |
||||||||||||||||
виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
dy |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
dt |
+ y = kz(e); |
|
(6.15) |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
e = v − y. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
При |
v = 0, y = −e |
движение |
|
системы |
можно описать одним |
|||||||||||
уравнением первого порядка |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
de |
= − |
e |
− |
k |
z(e) , |
|
(6.16) |
||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
dt |
|
T |
|
T |
|
|
|
|
|||||
в котором вместо переменной состояния |
y |
взято отличающееся от |
||||||||||||||
нее знаком рассогласование e .
Возьмем функцию Ляпунова в виде
151

V
=
1 |
e |
2 |
|
||
2 |
|
|
|
|
+
e z(ξ)dξ
0
,
(6.17)
тогда ее производная
dV dt
При e
=
z(
dV |
|
de |
= [e + z(e)] |
de |
= −[e + z(e)] |
e |
+ |
k |
z(e) |
|
= |
|
de |
dt |
dt |
|
T |
|
|||||||
|
|
|
|
|
|
|||||||
|
|
|
T |
|
|
|
|
|
e2 |
|
|
k |
z 2 |
|
1 + k |
|
|
||
= − |
|
+ |
|
|
(e) + |
|
|
ez(e) . |
(6.18) |
||
|
|
|
|
|
|||||||
|
T |
|
T |
|
|
|
T |
|
|
||
e) 0 |
производная отрицательна во всем пространстве, |
||||||||||
если k 0. Таким образом, достаточным условием асимптотической устойчивости в целом системы первого порядка с инерционным звеном является положительность коэффициента усиления линейной части. При этом характеристика нелинейного звена может иметь произвольный вид и лишь не должна выходить за пределы первого и третьего квадрантов (рис. 6.5, б). Она может иметь также разрывы, но должна быть однозначной (такие системы называются абсолютно устойчивыми).
Пример 6.4. Найти условия устойчивости положения равновесия в системе рис. 6.5, а, имеющей передаточную функцию линейной части
W |
( p) = |
л |
|
k p(1+
pT )
.
(6.19)
Решение. На рис. 6.6 показана структурная схема этой системы с
переменными состояниями x1 и |
x2 |
на выходах интегрирующих |
звеньев. Вместо
рассогласование |
e = |
|
−
переменной |
x1 |
удобнее |
рассматривать |
1 . |
|
|
|
x |
|
|
|
Рис. 6.6
152

Дифференциальные уравнения состояния системы имеют вид
|
de |
= −x2 |
; |
|
|||
|
dt |
|
|||||
|
|
|
|
|
|||
dx |
|
k |
|
|
1 |
|
|
2 |
= |
|
z(e) − |
|
x2 . |
||
dt |
T |
T |
|||||
|
|
|
|
||||
Возьмем функцию Ляпунова в виде
e
V = 0,5x22 + z( )d .
0
причем β 0 .
(6.20)
(6.21)
(6.22)
Выражение для производной dV / dt |
будет иметь вид |
dV |
= |
V de |
+ |
V |
dx |
2 |
= βz(e) |
de |
+ x |
dx |
2 |
, |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||
dt |
|
e dt |
|
x |
|
dt |
|
dt |
2 |
dt |
|||
|
|
2 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или после подстановки уравнений состояния
|
dV |
= −βz(e)x2 + |
k |
x2 z(e) − |
1 |
2 |
||
|
dt |
T |
T |
x2 . |
||||
|
|
|
|
|
|
|||
Выбирая |
β = k / T |
(это можно |
сделать |
при условии |
||||
(6.23)
(6.24)
k 0),
получаем отрицательность dV / dt во всем пространстве состояний, что свидетельствует об асимптотической устойчивости в целом положения равновесия. Интересно отметить, что и в этом примере характеристика нелинейного звена может иметь произвольный вид и лишь не должна выходить за пределы первого и третьего квадрантов, как это показано на рис. 6.5, б.
Пример 6.5. Пусть имеется система уравнений
dx |
= −(x − y)(1 |
− ax |
2 |
− by |
2 |
); |
|
|
dt |
|
|
|
|
||||
|
|
|
|
|
|
|
||
dy |
|
|
|
|
|
|
|
|
= −( y + αx)(1 − ax |
2 |
− by |
2 |
|
|
|||
|
|
|||||||
|
|
|
), |
|||||
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6.25)
где α , β , a и b – положительные постоянные коэффициенты.
Решение. Предположим для этой системы следующую функцию Ляпунова:
V = αx2 + βy2 .
Ее производная
dVdt = 2αx dxdt + 2βy dydt .
153

Подставив сюда выражение (6.25), получим
dV |
= −2(1 − ax |
2 |
− by |
2 |
)(αx |
2 |
+ βy |
2 |
) . |
||||
|
|||||||||||||
dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная dV / dt 0 при ax |
2 |
+ by |
2 |
1. |
|
|
|||||||
|
|
|
|
||||||||||
(6.26)
Это означает, что при выполнении условия (6.26) функция (6.25) является функцией Ляпунова, т. к. условие (6.26) представляет собой достаточное условие устойчивости системы. Границей устойчивости в фазовой плоскости является, следовательно, неустойчивой предельный цикл в виде эллипса
ax2 + by2 =1.
Необходимо также отметить, что если при отыскании функции Ляпунова функцию заданной формы удалось найти, то можно быть уверенным, что положение равновесия устойчиво. Если же это не удалось, это еще не означает, что равновесие неустойчиво, может просто оказаться, что функции Ляпунова данной формы не существует, но существует функция другого вида.
6.3. Критерий абсолютной устойчивости равновесия. Критерий устойчивости Попова
Абсолютной устойчивостью называют асимптотическую устойчивость положения равновесия системы в целом для нелинейностей, принадлежащих к определенному классу. Наиболее часто по предложению М. А. Айзермана, сделанному им в 1946 г., для систем со структурной схемой, показанной на рис. 6.5 а, рассматривают нелинейные характеристики, заключенные внутри
угла, образованного прямыми z = kx и |
z = rx |
(r k ) |
в первом и |
третьем квадрантах (рис. 6.5, а). Про такие нелинейные характеристики будем говорить, что они заключены в секторе [r, k].
В 1959 г. румынским математиком В. М. Поповым был предложен весьма простой и наглядный частотный критерий абсолютной устойчивости систем автоматического управления. Теория абсолютной устойчивости получила дальнейшее развитие в
работах |
М. А. Айзермана, |
|
В. А. Якубовича, |
А. X. Гелига, |
Я. З. Цыпкина, Б. Н. Наумова |
и |
других в СССР, |
Дж. Ла-Салля, |
|
С. Лефшеца, Р. Калмана в США и |
в ряде других исследований. |
|||
154

Критерий абсолютной устойчивости формулируется следующим образом: если замкнутая система (см. рис. 6.5, а) состоит из
устойчивой линейной части с передаточной функцией |
Wл ( p) , все |
полюса которой расположены в левой полуплоскости, и однозначной нелинейности z(x) , лежащей, в угле 0 z(x) / x k (сектор [0, k], рис.
условием устойчивости является
Re[1 + jqωW |
( jω)] + |
1 |
|
||
л |
|
k |
|
|
где q – произвольное вещественное число. При этом имеется в виду, что
=
k
δ
0,
.
a
(6.27)
lim Wл ( jω) = 0 . ω→
Последнее условие вытекает из правильного учета малых параметров нелинейности или грубости рассматриваемой системы.
Критерию абсолютной устойчивости можно дать удобную для практики геометрическую интерпретацию. Подставив в (6.27) выражение
Wл ( jω) = Pл (ω) + jQл (ω) ,
получим
P (ω) − qωQ |
|
(ω) + |
1 |
= δ 0 . |
|
л |
|
||||
л |
|
|
k |
||
|
|
|
|
||
Введем понятие |
преобразованной частотной |
||||
линейной части |
|
|
|
|
|
Wл.п ( jω) = Pл (ω) + jωQл (ω) . |
|||||
(6.28)
(6.29)
характеристики
(6.30)
Эта характеристика получается из частотной характеристики W ( jω) линейной части системы путем умножения ординат этой характеристики на текущее значение частоты ω .
Если построить годограф Wл.п ( jω) и здесь же провести прямую, описываемую уравнением
Pл (ω) = − |
1 |
+ qωQл (ω), |
|
k |
|||
|
|
то условием выполнения, неравенства (6.29) будет годографа Wл.п ( jω) справа от этой прямой (рис. 6.7, в).
(6.31)
расположение
Таким образом, для критерия абсолютной устойчивости можно дать следующую формулировку: система абсолютно устойчива,
если при устойчивой линейной части через точку (−1/ k, j0) можно провести прямую так, чтобы годограф Wл.п ( jω) лежал справа от
155
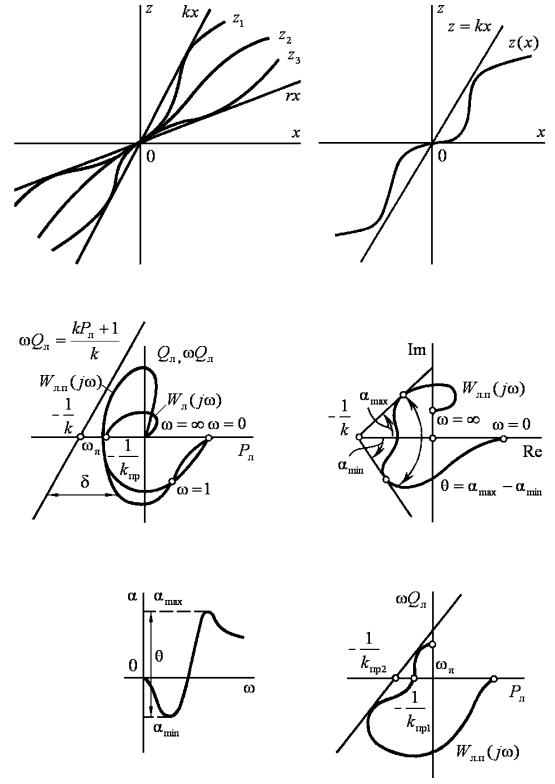
нее. Прямую, удовлетворяющую этому условию, называют прямой Попова.
а |
б |
в |
г |
д |
е |
Рис. 6.7
156
Условие (6.29) должно выполняться для одном значении q , лежащем в диапазоне ( −
( 0 ω
q + ).
) хотя бы при
При решении задачи об абсолютной устойчивости конкретной системы с заданным значением k и известной функцией Wл ( jω)
необходим перебор двух координат ω и q и проверка выполнения
неравенства (6.29) во всем диапазоне возможных значений
ω
и
q
.
Рассматриваемая геометрическая интерпретация неравенства (6.27)
не изменяет этого положения. |
Построение годографа Wл.п ( jω) и |
проведение прямых с наклоном |
q через точку −1/ k по-прежнему |
предусматривает перебор координат ω и q .
Критерий абсолютной устойчивости не выполняется, если происходит касание характеристик или если характеристика Wл.п ( jω)
охватывает точку (−1/ k, j0) .
Естественное продолжение рассуждений, связанных в геометрической интерпретацией неравенства (6.29), приводит к иной аналитической формулировке критерия абсолютной устойчивости. Вместо неравенства (6.29) можно предложить следующее:
θ = α |
max |
− α |
min |
|
|
π
,
(6.32)
где
α
=
arg[W |
(ω) |
л.п |
|
+1/
k
]
;
αmax
и
α min
максимальное и минимальное
значения α при 0 ω . В этом неравенстве содержится только одна переменная координата ω и его выполнение предусматривает перебор только по этой координате (рис. 6.9, г, д). Параметр q был
введен только для доказательства критерия и при пользовании критерием абсолютной устойчивости можно обойтись без него.
Предложение о формулировке критерия в виде неравенства (6.32) возникло в связи с машинным проектированием нелинейных систем. Применение неравенства (6.32) позволяет значительно упростить алгоритм решения задачи.
Критерий В. М. Попова является достаточным, т. е. он дает часть области абсолютной устойчивости и его невыполнение не означает еще неустойчивость.
Интересно сравнить условия абсолютной устойчивости В. М. Попова с условиями устойчивости линейной системы, получаемой при предположении, что характеристика z(x) в секторе
[0, k] является линейной. Это значит, что нелинейное звено
157
