
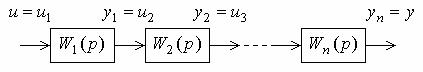
5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ОДНОМЕРНЫХ САУ
5.1. Основные виды соединений звеньев САУ, их передаточные функции
Врезультате разбиения САУ на звенья направленного действия
иполучения математического описания звеньев в виде передаточных функций, частотных или переходных характеристик составляется структурная схема системы. По структурной схеме можно затем
получить передаточные функции или характеристики системы в целом.
Если имеются уравнения всех звеньев системы, то описанием последней является система этих уравнений. Исключив из нее обычным порядком промежуточные переменные, можно получить одно дифференциальное уравнение высокого порядка, связывающее интересующую нас выходную величину системы с определенной входной величиной – каким-либо возмущением или задающим воздействием. Наиболее просто эту процедуру можно выполнить, если оперировать передаточными функциями звеньев.
5.1.1. Последовательное соединение звеньев. Такое соединение звеньев показано на рис. 5.1.
Рис. 5.1. Последовательное соединение звеньев
В этом случае имеем систему уравнений отдельных звеньев y1 W1(p)u1;
y2 W1(p)u2;
yn Wn(p)un,
а также уравнений связей между ними
97
u u1; y1 u2;
y yn.
Исключив отсюда промежуточные переменные, получим: y [W1(p)W2(p) Wn(p)]u W(p)u,
где
n |
|
W(p) Wi(p). |
(5.1) |
i 1 |
|
Следовательно, передаточная функция цепочки последовательно соединенных звеньев равна произведению передаточных функций звеньев. Это значит, что такую цепочку можно заменить в структурной схеме одним эквивалентным звеном с передаточной функцией W(p).
В качестве примера можно рассмотреть последовательное
соединение идеального |
дифференцирующего |
звена W1(p) k1p |
|
и инерционного звена |
первого |
порядка |
W2(p) k2 /(Tp 1). |
В результате получаем реальное дифференцирующее звено |
|||
W(p) W1(p)W2(p) kp/(Tp 1), |
(k k1k2). |
|
|
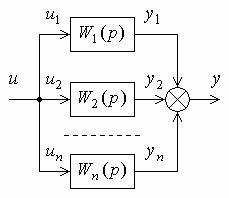
5.1.2. Параллельное соединение звеньев. Такое соединение звеньев показано на рис. 5.2.
Рис. 5.2. Параллельное соединение звеньев
98
В этом случае также система уравнений отдельных звеньев y1 W1(p)u1;
y2 W1(p)u2;
yn Wn(p)un,
а уравнения связей между ними
u u1 u2 un;
n
y y1 y2 yn yi .
i 1
Исключив отсюда промежуточные переменные, получим y [W1(p) W2(p) Wn(p)]u W(p)u,
где
n |
|
W(p) Wi(p). |
(5.2) |
i 1 |
|
Таким образом, передаточная функция группы |
параллельно |
соединенных звеньев равна сумме передаточных функций отдельных звеньев. В структурной схеме такую группу звеньев можно заменить одним эквивалентным звеном с соответствующей передаточной функцией W(p).
В качестве примера можно рассмотреть параллельное соединение двух звеньев. Пусть передаточная функция первого звена
W1(p) k1, второго – W2(p) k2 p. Тогда |
|
W(p) W1(p) W2(p) k1 k2 p k(Tp 1), |
(k k1;T k2 /k1). |
Следовательно, параллельное соединение пропорционального
идифференцирующего звеньев образует форсирующее звено.
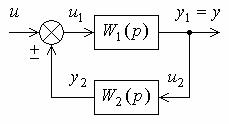
5.1.3.Звено, охваченное обратной связью. Такое соединение звеньев показано на рис. 5.3.
Рис. 5.3. Звено, охваченное обратной связью
99
Обратная связь может быть положительной, если сигнал обратной связи y2 складывается с входным сигналом u (плюс у суммирующего элемента на рис. 5.3, в), или отрицательной, если y2 вычитается из u (минус на рис. 5.3, в). Схема описывается следующими уравнениями:
y1 W1(p)u1; y2 W1(p)u2; u1 u y2;
y y1 u2.
Здесь в третьем уравнении знак плюс соответствует положительной обратной связи, а знак минус – отрицательной. Исключив отсюда промежуточные переменные, получим:
y |
|
W1(p) |
|
u Ф(p)u, |
|
||
|
|
|
|
|
|||
где |
1 W1(p)W2(p) |
|
|||||
|
|
|
W1(p) |
|
|
||
|
|
Ф(p) |
|
; |
(5.3) |
||
|
|
|
|
||||
|
1 |
W(p) |
|
||||
|
|
W(p) W1(p)W2(p). |
(5.4) |
||||
Здесь положительной обратной связи соответствует минус, отрицательной – плюс.
Функция Ф(p) называется передаточной функцией замкнутой системы, a W(p) – передаточной функцией разомкнутой системы, т. е. цепочки из всех звеньев системы, получающейся после разрыва обратной связи.
В качестве примера рассмотрим интегрирующее звено с передаточной функцией W1(p) k1 / p, охваченное отрицательной обратной связью через идеальное статическое звено с передаточной функцией W2(p) k2. Обратная связь, осуществляемая через статическое звено, называется жесткой обратной связью. Согласно
(5.3)
Ф(p) |
k1 / p |
|
k |
, k 1/k |
2 |
, |
T 1/k k |
2 |
. |
|
|
||||||||
1 k1k2 / p |
|
Tp 1 |
|
1 |
|
||||
|
|
|
|
|
|
||||
Таким образом, интегрирующее звено, охваченное жесткой обратной связью, эквивалентно апериодическому звену, т. е. не является уже интегрирующим.
100
5.2. Передаточные функции одноконтурной САУ |
|
|||||
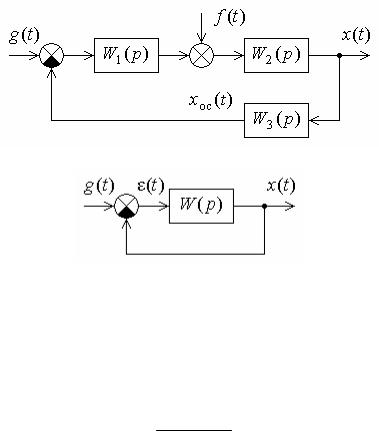
Структурная |
схема |
одноконтурной |
САУ |
приведена |
на |
|
рис. 5.4, а, где x |
– интересующая нас |
выходная |
величина, |
g – |
||
задающее воздействие, f |
– возмущение. Выведем выражение для |
|||||
передаточных функций, |
связывающих |
x c |
g и |
f . Для этого |
||
достаточно воспользоваться (5.3), учитывая при этом, что в САУ общая обратная связь, создающая замкнутый контур системы, всегда отрицательная. Это определяется самим принципом действия САУ, управляющее устройство которых осуществляет управление объектом в функции отклонения x от его значения, определяемого заданием g. При этом именно за счет того, что управляющее устройство осуществляет отрицательную обратную связь, все изменения выходной величины объекта, вызванные каким-либо возмущением, будут ликвидироваться в результате противоположного действия управляющего устройства.
а
б
Рис. 5.4. Структурные схемы одноконтурных САУ
Итак, с учетом сказанного, согласно (5.3), в общем случае одноконтурной САУ
x Wxf (p) f , 1 W(p)
т. е. передаточная функция замкнутой САУ, связывающая выходную величину x с внешним воздействием f , приложенным
101

в произвольной точке системы, имеет следующий вид:
Фf (p) |
x |
Wxf (p) |
|
||
|
|
|
. |
(5.5) |
|
|
|
||||
|
f |
1 W(p) |
|
||
Здесь числитель Фf (p)представляет собой передаточную функцию
Wxf (p), определяющую, как показывают индексы, зависимость x от f при отсутствии обратной связи. Эта передаточная функция зависит от места нахождения x и f в системе. Знаменатель Фf (p) включает в себя передаточную функцию разомкнутой системы W(p) и не зависит от места нахождения x и f .
Для схемы, изображенной на рис. 5.4, а,
Wxf (p) W2(p), W(p) W1(p)W2(p)W3(p)
Индекс f у передаточной функции замкнутой системы Фf (p)
показывает, к какому внешнему воздействию она относится.
Всоответствии с (5.5) передаточная функция, связывающая x
сзадающим воздействием g,
Фg (p) |
x |
|
Wxg (p) |
|
||
|
|
|
|
, |
(5.6) |
|
|
|
|||||
|
g |
1 W(p) |
|
|||
где для схемы, показанной на рис. 5.4, а,
Wxg (p) W1(p)W2(p).
В общем случае, когда на систему действует одновременно несколько возмущений, на основе принципа суперпозиции получаем:
|
|
Wxfi |
(p)fi |
|
|
x Фfi |
(p)fi |
i |
|
. |
(5.7) |
|
|
||||
i |
|
1 W(p) |
|
||
В частности, для системы, изображенной на рис. 5.4, а, при одновременном действии на нее f и g
x |
Wxf (p)f Wxg (p)g |
(5.8) |
. |
1 W(p)
В распространенном частном случае систем автоматического регулирования – в следящих системах, задачей которых явяется обеспечение слежения величиной x за величиной g, обычно Wxg (p) W(p), т. е. структурная схема системы соответствует
102
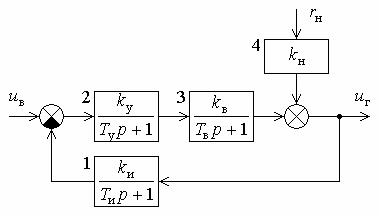
рис. 5.4, б. Такая система называется системой с единичной обратной связью. В этом случае (5.6) принимает вид:
Фg (p) |
W(p) |
. |
(5.9) |
|
|||
1 W(p) |
|
||
При исследовании систем автоматического регулирования часто, помимо выходной величины x, интерес представляет величина ошибки
ε g x.
Подставив полученное согласно (5.6) выражение x Фg (p)g,
будем иметь передаточную функцию системы по ошибке
Фε(p) |
ε |
|
1 |
|
. |
(5.10) |
g |
1 W |
|
||||
|
|
(p) |
|
|||
В частности, величина ε, определяемая по этой формуле, широко используется при исследовании точности следящих систем
(рис. 5.4, б).
Пример 5.1. Необходимо написать выражения для передаточных функций системы автоматического регулирования напряжения синхронного генератора. Структурная схема системы приведена на рис. 5.5. В схему входят три апериодических звена: звено 1 – измеритель напряжения, звено 2 – усилитель и звено 3 – генератор, являющийся объектом регулирования. В качестве внешних воздействий на схеме указаны изменение задающего воздействия uз, определяющего регулируемое значение напряжения, и изменения активного сопротивления нагрузки rн.
Рис. 5.5. Структурная схема системы автоматического регулирования напряжения синхронного генератора
103
Решение. Согласно (5.5) получаем передаточную функцию для возмущения
|
|
|
Фr |
(p) |
uг |
|
|
kн |
, |
|
|
|||
|
|
|
|
|
|
|||||||||
|
|
|
|
н |
|
|
rн |
1 W(p) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
kиkуkв |
|
|
|
k |
|
||||||||
W(p) |
|
|
|
|
. |
|||||||||
(Tи p 1)(Tв p 1)(Tв p 1) |
|
(Tи р 1)(Tу p 1)(Тв p 1) |
||||||||||||
|
|
|
|
|||||||||||
После освобождения от дроби в знаменателе |
|
|
|
|||||||||||
|
Фr |
(p) |
uг |
|
kн(Tи p 1)(Tу p 1)(Тв p 1) |
. |
|
|||||||
|
rн |
|
|
|||||||||||
|
н |
|
|
|
(Tи р 1)(Tу p 1)(Тв p 1) k |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если раскрыть скобки в числителе и знаменателе, получим многочлены третьего порядка.
Передаточная функция для задающего воздействия
|
|
|
|
|
|
|
kуkв |
|
|
|
|
Ф |
u |
|
(p) |
uг |
|
(Tу p 1)(Тв p 1) |
|
|
kуkв(Tи p 1) |
. |
|
з |
uз |
|
|
(Tи р 1)(Tу p 1)(Тв p 1) k |
|||||||
|
|
|
|
1 W(p) |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Таким образом, числитель второй передаточной функции имеет первый порядок.
5.3. Правила структурных преобразований САУ
Если одномерная система содержит произвольное число связанных друг с другом контуров управления, то запись ее передаточных функций возможна с помощью преобразования исходной многоконтурной схемы в эквивалентную одноконтурную. При проведении указанного преобразования структурной схемы системы руководствуются рядом правил. В их число входят, прежде всего, уже изложенные выше правила замены групп последовательно и параллельно соединенных звеньев, а также звена с обратной связью одним эквивалентным звеном. Кроме того, применяются правила переноса звеньев или воздействий из одной точки системы в другую. Эти правила очевидны и вытекают из условия сохранения значений сигналов на выходе схемы при выполнении соответствующих преобразований.
104
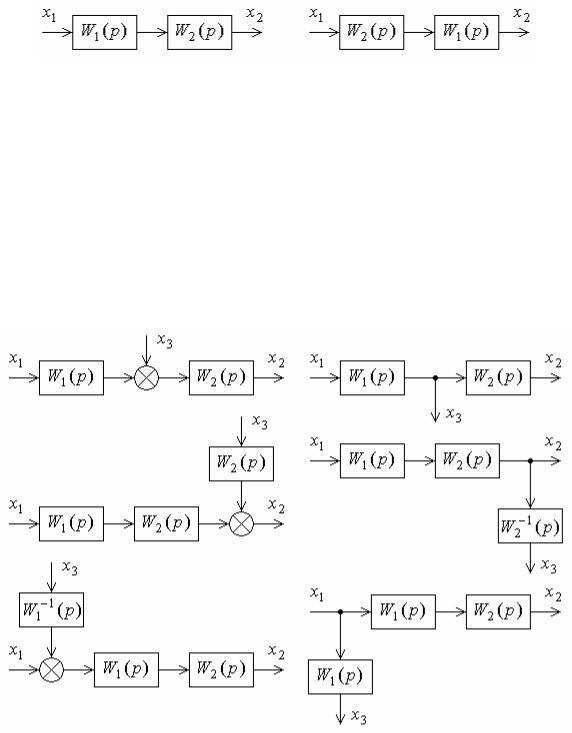
Последовательно соединенные стационарные линейные звенья можно менять местами (рис. 5.6).
Рис. 5.6
Как показано на рис. 5.7, при перенесении суммирующего элемента, т. е. выхода параллельной ветви, вперед (по стрелке
основного контура) в |
ветвь |
добавляется |
фиктивное |
звено |
с передаточной функцией |
W2(p) |
обойденного |
при этом |
звена |
основного контура. При перенесении суммирующего элемента назад добавляется звено с обратной передаточной функцией 1/W1(p). Нетрудно видеть, что в обоих случаях сигнал на выходе рассматриваемой части основного контура сохраняется неизменным.
Рис. 5.7 Рис. 5.8
При перенесении точки разветвления, т. е. входа параллельной ветви (рис. 5.8), правило преобразования обратное: при переносе этой точки вперед в ветвь добавляется звено с обратной передаточной
105
функцией 1/W2(p) обойденного звена, а при переносе назад – звено с передаточной функцией W1(p).
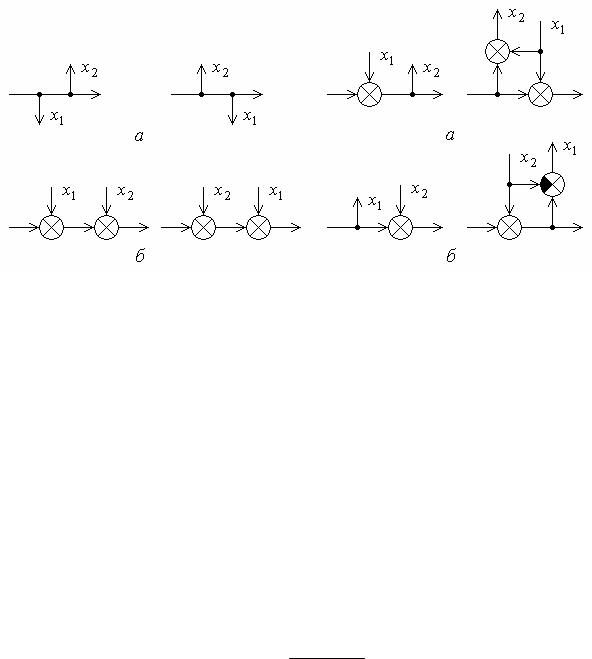
Два узла можно всегда менять местами (рис. 5.9, а), два сумматора можно всегда менять местами (рис. 5.9, б).
При перемещении суммирующего узла через узел разветвления по направлению ветвления необходимо в отводящих от разветвления ветвях добавить такие же, как и перемещаемый узел, суммирующие узлы (рис. 5.10, а); при перемещении наоборот – узлы с обратными знаками (рис. 5.10, б).
Рис. 5.9 |
Рис. 5.10 |
В системе с обратной связью можно менять местами звенья, находящиеся в прямой цепи и обратной связи, заменив при этом оба звена соответствующими обратными звеньми (рис. 5.11). Для перехода системы с обратной связью к системе с единичной обратной связью, звено в обратной связи включается в прямую связь системы и обратное ему звено включается на вход системы (рис. 5.12).
Основной задачей преобразования многоконтурной структурной схемы является приведение ее к схеме с неперекрещивающимися связями, когда отдельные контуры схемы не сцепляются друг с другом. После этого каждый из этих контуров может быть заменен одним эквивалентным звеном с передаточной функцией, определенной по формуле
Ф(p) W1(p) . 1 W(p)
В результате исходная схема приводится к одноконтурной.
106
