
Рис. 5.11 |
Рис. 5.12 |
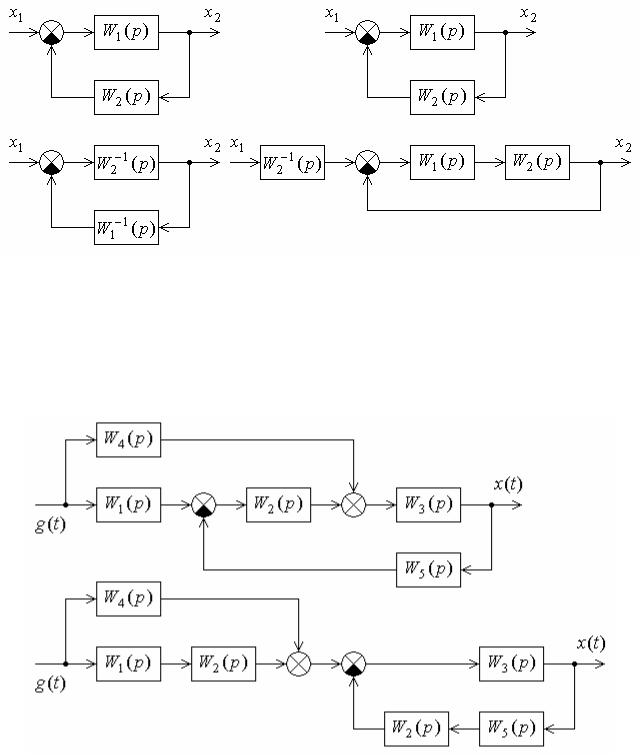
Пример 5.2. На рис. 5.13 дан пример преобразования структурной схемы САУ комбинированного управления с перекрещиванием прямой связи с обратной.
Рис. 5.13. Пример преобразования структурной схемы
Решение. Изображенное на рис. 5.13 последовательное преобразование схемы начинается с переноса вперед элемента сравнения. При этом в цепь обратной связи добавляется звено с передаточной функцией W2(p). В результате перекрещивание связей пропадает.
107

Далее объединяются в одно звено звенья W1(p), W2(p) и W4(p)
WI(p) W1(p)W2(p) W4(p),
а также звенья W2(p), W3(p) и W5(p)
WII(p) W3(p) . 1 W3(p)W2(p)W5(p)
После этого уже может быть написано выражение для общей передаточной функции
Ф(p) WI(p)WII(p) [W1(p)W2(p) W4(p)]W3(p). 1 W3(p)W2(p)W5(p)
Тот же результат можно получить и путем переноса назад сумматора с добавлением в параллельную цепь нового звена
с передаточной функцией 1/W2 1(p).
5.4. Математическое описание многоконтурных САУ
Другой метод получения выражения для передаточной функции сложной многоконтурной системы заключается в применении формулы Мейсона, которая приводится без доказательства.
Ф(p) |
1 |
Wпрi(p) i(p). |
(5.11) |
|
(p) |
||||
|
i |
|
Здесь Wпрi(p) – передаточные функции отдельных прямых путей от
входа к выходу схемы, т. е. от входного воздействия к выходной величине; (p) – определитель системы
(p) 1 Wi(p) Wi(p)Wj(p) Wi(p)Wj(p)Wk (p) ,
где Wi(p) |
– |
сумма передаточных |
функций всех контуров; |
Wi(p)Wj(p) |
и |
Wi(p)Wj(p)Wk (p) – |
суммы произведений двух, |
трех и т. д. передаточных функций контуров, не соприкасающихся друг с другом; i(p) – это (p) после изъятия из схемы i-го прямого пути (при этом пропадают параллельные другие пути, начинающиеся или заканчивающиеся в общих с этим путем точках).
Все передаточные функции в (5.11) должны писаться со знаком плюс или минус в зависимости от знака сигналов на выходе соответствующих звеньев в структурной схеме.
108
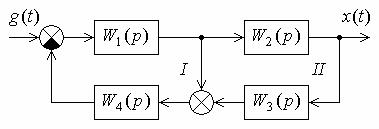
Пример 5.3. Продемонстрируем применение формулы Мейсона на примере схемы системы, показанной на рис. 5.14.
Рис. 5.14. Пример многоконтурной схемы
Решение. Здесь имеются два контура, обозначенных I , II и один прямой путь. Передаточные функции контуров:
WI (p) W1(p)W4(p);
WII (p) W1(p)W2(p)W3(p)W4(p).
Передаточная функция прямого пути:
Wпр1(p) W1(p)W2(p).
Знаменатель искомой передаточной функции, (p) 1 WI(p) WII(p)
1 W1(p)W4(p) W1(p)W2(p)W3(p)W4(p).
Сизъятием из системы прямого пути контуров не остается,
поэтому
1(p) 1.
Для получения искомого выражения для Ф(p) необходимо подставить приведенные выше выражения в (5.11)
Wпр1(p) 1 |
(p) |
|
W (p)W (p) |
|
||
Ф(p) |
|
|
|
|
1 2 |
. |
(p) |
|
1 W1(p)W4(p) W1(p)W2(p)W3(p)W4(p) |
||||
|
|
|
|
|||
Для САУ, рассмотренной в примере 5.2, можно выделить два прямых пути и один контур. В результате получим:
Wпр1(p) W1(p)W2(p)W3(p);
Wпр2(p) W4(p)W3(p);
(p) 1 W3(p)W2(p)W5(p);1(p) 2(p) 1.
109

Тогда искомая передаточная функция
Ф(p) Wпр1(p) 1(p) Wпр2(p) 2(p)(p)
[W1(p)W2(p) W4(p)]W3(p). 1 W3(p)W2(p)W5(p)
По найденной передаточной функции одномерной замкнутой системы, имеющей вид выражения
|
|
Wxfi |
(p)fi |
|
x Фfi |
(p)fi |
i |
|
, |
|
|
|||
i |
|
1 W(p) |
||
легко получить записанное в обычной форме дифференциальное уравнение системы. Для этого надо предварительно освободиться в числителе и знаменателе этого выражения от дробей:
|
R(p) |
Rxf i(p) |
||
W(p) |
|
и Wxfi(p) |
|
. |
|
|
|||
|
Q(p) |
Qxf i(p) |
||
В результате получим уравнение |
|
|
||
|
|
n |
|
|
D(p)x Mi(p)fi , |
(5.12) |
|||
|
|
i 1 |
|
|
где D(p) R(p) Q(p), |
а Mi(p) зависят от места приложения |
|||
воздействий fi. |
|
|
|
|
5.5. Построение частотных характеристик САУ по частотным характеристикам звеньев
Связь между |
частотными характеристиками системы |
и составляющих ее |
звеньев определяется выражением для |
передаточной функции, если подставить в него p jω:
W(jω) W(p)|p jω.
Соответственно амплитудно-фазовая частотная характеристика цепочки последовательно соединенных звеньев разомкнутой системы согласно (5.1)
W(jω) Wi( jω), |
(5.13) |
i |
|
110
где Wi(jω) – амплитудно-фазовая частотная характеристика i-го
звена цепочки. Отсюда W(jω) Aej Aiej i , тогда
i
A(ω) Ai(ω); |
(5.14) |
i |
|
(ω) i(ω), |
(5.15) |
i |
|
где A(ω) и (ω) – амплитудная и фазовая характеристики цепочки звеньев, а Ai(ω) и i(ω) – это характеристики i-го звена.
Логарифмирование первого равенства (5.13) дает следующее выражение для логарифмической амплитудной характеристики цепочки звеньев:
L(ω) 20lg A(ω) Li(ω), |
(5.16) |
i |
|
где Li(ω) – ЛАХ отдельного звена.
Как следует из (5.16) и (5.17), наиболее просто строятся частотные характеристики цепочки звеньев в виде ЛАХ и ЛФХ: они получаются путем суммирования ординат характеристик отдельных звеньев.
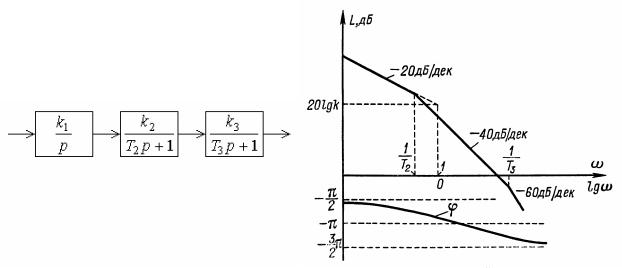
Пример 5.4. На рис. 5.15 в качестве примера приведены ЛАХ и ЛФХ цепочки последовательно соединенных одного интегрирующего и двух апериодических звеньев, где k1k2k3 k, T2 T3.
а |
б |
Рис. 5.15. ЛАХ и ЛФХ цепочки последовательно соединенных звеньев
111
Решение. ЛАХ цепочки звеньев строится сразу без построения ЛАХ отдельных звеньев. Вначале откладывается ордината общей ЛАХ при ω 1, равная 20lgk , где k – коэффициент передачи всей цепочки звеньев, равный произведению коэффициентов передачи звеньев. Затем через найденную точку проводится асимптота с наклоном 20(m r) дБ/дек, где m – число дифференцирующих, а r
– число интегрирующих звеньев. После этого на оси абсцисс откладываются значения сопрягающих частот, равных 1/Ti , где Ti – постоянные времени звеньев. Напомним, что на оси абсцисс удобно указывать наряду с lgω непосредственно и значения ω. Далее первая асимптота проводится от оси ординат до наименьшей сопрягающей частоты. В этой точке производится ее излом с изменением наклона в соответствии с типом звена, которому принадлежит данная сопрягающая частота.
Таким же образом характеристика продолжается в сторону увеличения частоты, претерпевая последовательно изломы на каждой сопрягающей частоте. При необходимости построенная ЛАХ уточняется путем учета поправок для колебательных звеньев.
Ординаты ЛФХ звеньев |
суммируются |
обычным |
способом. |
В результате предельное значение цепочки звеньев, |
получаемое |
||
при ω , будет равно |
(n m)π/2, |
где n |
– порядок |
дифференциального уравнения цепочки, а m – число идеальных дифференцирующих звеньев.
Построение амплитудно-фазовой характеристики цепочки звеньев непосредственно по амплитудно-фазовым характеристикам отдельных звеньев осуществляется в соответствии с (5.14) путем перемножения векторов Wi(jω) при одинаковых значениях частоты. При этом модули Ai(ω)перемножаются, а фазы i(ω) – складываются. АФЧХ последовательно соединенных звеньев представлены на рис. 5.16, где 1, 2, 3 и 4 – соответственно для одного, двух, трех и четырех апериодических звеньев, а 5 – для трех апериодических звеньев и одного идеального интегрирующего звена.
112

Рис. 5.16. АФЧХ цепочки последовательно соединенных звеньев
Амплитудно-фазовая характеристика группы параллельно
соединенных звеньев |
|
W(jω) Wi(jω). |
(5.17) |
i |
|
Соответственно она строится путем геометрического суммирования векторов Wi(jω) при одинаковых частотах.
Амплитудно-фазовая характеристика звена с обратной связью
Ф( jω) |
W1(jω) |
. |
(5.18) |
|
|||
1 W(jω) |
|
||
Оперируя векторами W1( jω)и W( jω) в соответствии с этим выражением, можно графически построить амплитудно-фазовую характеристику звена с обратной связью Ф( jω) по амплитуднофазовым характеристикам звеньев без обратной связи W1( jω) и разомкнутого контура W(jω) W1( jω)W2(jω).
Последняя характеристика предварительно строится как характеристика цепочки последовательно соединенных звеньев, входящих в контур и описываемых функциями W1( jω) и W2( jω).
Практически в большинстве случаев задача построения логарифмических частотных характеристик звена с обратной связью существенно упрощается благодаря наличию номограмм, позволяющих по известным логарифмическим характеристикам разомкнутого контура W( jω) получить логарифмические характеристики замкнутого контура Ф( jω) для случая, когда
Ф( jω) W(jω) . 1 W(jω)
113

Для того чтобы использовать эти номограммы в более общем случае отрицательной обратной связи через звено с произвольной передаточной функцией, выражение
Ф( jω) W1(jω) , 1 W(jω)
где
W(jω) W1(jω)W2( jω),
надо предварительно привести к следующему виду:
Wр(jω) |
|
|
Ф( jω) |
|
W1(jω), |
1 W (jω) |
||
|
р |
|
|
|
|
где
W (jω) 1 . |
|
р |
W(jω) |
|
|
По номограммам могут быть найдены логарифмические характеристики для выражения, стоящего в квадратных скобках. После этого искомые характеристики легко определяются по только что найденным характеристикам и характеристикам, соответствующим W1( jω), как в случае последовательно соединенных звеньев.
Пример 5.5. Найти передаточную функцию Ф(p) замкнутой автоматической системы управления, структурная схема которой изображена на рис. 5.17.
Решение. Освободимся от перекрестных связей в структурной схеме на рис. 5.17, для чего перенесем узел 1 через звено W3(p) по направлению действия сигнала. При этом получаем систему с тремя вложенными друг в друга контурами обратной связи.
Передаточная функция внутреннего замкнутого контура:
|
|
|
Ф (p) |
W2(p)W3(p) |
. |
|
||||
|
|
|
|
|
|
|||||
|
|
|
|
1 |
1 W2(p)W3(p) |
|||||
|
|
|
|
|
||||||
Передаточная функция второго замкнутого контура: |
||||||||||
Ф2(p) |
|
W1(p)Ф1(p) |
|
|
|
W1(p)W2(p)W3(p) |
||||
|
|
|
|
|
. |
|||||
1 W (p)Ф (p)W 1 |
(p) |
1 W2(p)W3(p) W1(p)W2(p) |
||||||||
|
1 |
1 |
3 |
|
|
|
|
|
|
|
114
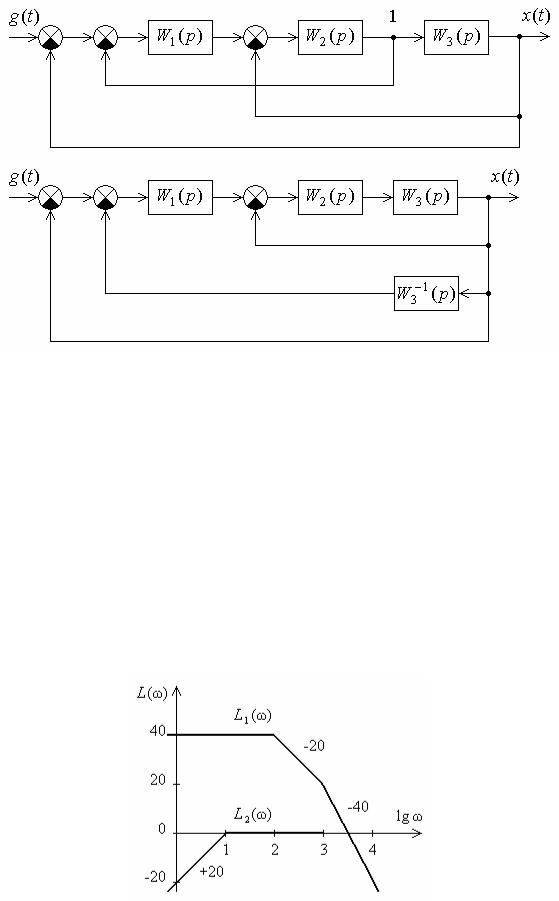
Рис. 5.17
Передаточная функция внешнего замкнутого контура:
|
|
Ф(p) Ф3(p) |
Ф2(p) |
|
|
|
|
||||
|
|
1 Ф2(p) |
|
|
|
|
|
W1(p)W2(p)W3(p) |
|
. |
|
|
|
|
|||
|
1 W1(p)W2(p) W2(p)W3(p) W1(p)W2(p)W3(p) |
||||
Пример 5.6. На рис. 5.18 изображены асимптотические логарифмические амплитудные характеристики минимально-фазовых звеньев. Найти передаточные функции этих звеньев.
Рис. 5.18
115

Решение. По виду низкочастотных асимптот первое звено является статическим звеном, второе – дифференцирующим.
Для первого звена:
L1(ω)|ω 1 20lgk1 40. |
Тогда |
k1 100. |
Точки излома ЛАХ: |
|||||
lgω1 2; |
lgω2 3. |
Тогда |
T1 1/ω1 1/100 0,01с; |
T2 1/ω2 |
||||
1/1000 0,001с. |
|
|
|
|
|
|
|
|
Следовательно, передаточная функция первого звена: |
||||||||
|
W1(p) |
|
100 |
|
. |
|
||
|
|
|
|
|
|
|||
|
|
|
(0,01p 1)(0,001p 1) |
|
||||
Для второго звена: |
|
k2 0,1с. |
|
|
|
|||
L1(ω)|ω 1 20lgk2 |
20. |
Тогда |
Точка излома ЛАХ: |
|||||
lgω3 1. Тогда T3 1/ω3 1/10 0,1с.
Следовательно, передаточная функция второго звена:
W2(p) 0,1p . 0,1p 1
Контрольные вопросы
1.Назовите основные виды соединений звеньев САУ.
2.Чему равна передаточная функция группы последовательно соединенных звеньев?
3.Чему равна передаточная функция группы параллельно соединенных звеньев?
4.Чему равна передаточная функция звена, охваченного обратной связью?
5.Основные правила структурных преобразований систем управления?
6.В каком случае можно менять местами последовательно соединенные звенья?
7. Как преобразовать систему с обратной связью к системе
сединичной обратной связью?
8.Как определить передаточную функцию системы с помощью формулы Мейсона?
9. Как связана амплитудно-фазовая частотная характеристика с передаточной функцией?
116
