
8.ОПТИМАЛЬНЫЕ САУ
8.1.Постановка задачи оптимального управления
Под оптимальной автоматической системой управления
понимается наилучшая в некотором определенном смысле система. Критерии оптимальности, на основе которых строится система, могут быть самыми разными и зависят от специфики решаемой задачи. В практике автоматического управления в качестве критериев оптимальности встречаются: точность автоматической системы управления при изменяющихся входных сигналах, время переходного процесса, интегральные критерии переходного процесса, экономичность, производительность, сложность системы управления
идругие технико-экономические показатели.
Кнастоящему времени наибольшее развитие получили два направления в теории оптимальных систем. Первое – это теория оптимального управления движением системы с полной информацией об объекте и возмущениях, а второе – это теория оптимального управления при случайных возмущениях.
Нужно отметить, что в развитии первого направления теории много сделано советским ученым А. А. Фельдбаумом, которому принадлежит заслуга в постановке и решении многих важных задач в этой области. Принципы оптимального управления получают все большее распространение на практике. Они позволили создать новые автоматические регуляторы, следящие системы и другие устройства, которые существенно повышают эффективность промышленных систем автоматики.
Рассмотрим задачи оптимального управления при полной информации об объекте и возмущениях. Будем полагать, что объект управления линейный, полностью описан математически и его свойства менять нельзя, а управляющее устройство можно выбирать в определенных пределах. Возможности управляющего устройства, конечно, ограничиваются исходя из специфики задачи. Как правило, ограничения наложены на управляющие воздействия и на фазовые координаты системы. Чаще всего ограничения задаются в виде систем неравенств. Для управляющих воздействий такие неравенства можно записать в виде
Mi (u) = Mi (ui , ..., ur ) 0 |
(i =1, , r) , |
(8.1) |
|
|
193 |
где
|
|
d |
k −1 |
|
|
|
|
|
uk = |
|
u |
(k =1, , r). |
(8.2) |
||
|
dt |
k −1 |
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
||
В дальнейшем часто будем использовать обозначения типа (8.2). |
|||||||
Вектор управления u , подчиненный неравенствам (8.1), |
|||||||
принадлежит |
некоторой |
|
|
области |
(u) , |
ограниченной |
|
гиперповерхностью Mi (u) = 0 |
(i =1, , r) , что будем обозначать |
||||||
|
|
|
|
u (u) . |
|
(8.3) |
|
Управления, удовлетворяющие условиям (8.1) или (8.3),
называются допустимыми.
а
б
в
г
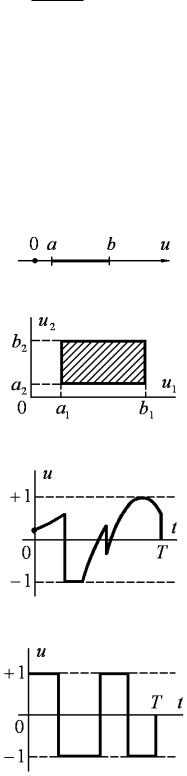
Рис. 8.1
194
Например, если управление ограничено только |
по величине |
a u b , то областью допустимых управлений будет |
отрезок ab |
(рис. 8.1, |
а). Если ограничены величина и производная управления |
||
системой |
неравенств |
a1 u1 b1, |
a2 u2 b2 , то областью |
допустимых управлений будет прямоугольник (рис. 8.1, б). Когда ограничена только величина управления снизу и сверху, то для последующих задач будет удобно полагать, что ограничение на управление имеет вид неравенства
 u
u 
1
.
(8.4)
К такой записи ограничений, как правило, можно перейти, сдвигая начало отсчета и изменяя масштаб величины u .
Ограничению типа (8.4) могут удовлетворять функции, имеющие разрывы первого рода. Если на вcем интервале времени
[0, Т], в |
течение |
которого осуществляется |
управление, число |
|
разрывов |
функции |
u(t) |
конечно, то такую |
функцию называют |
кусочно-непрерывной (рис. 8.1, в). Практически важным частным случаем кусочно-непрерывных функций являются кусочно-
постоянные функции, для которых u(t) |
поочередно равняется + 1 или |
|
−1 |
(рис. 8.1, г). Когда хотят охарактеризовать кусочно-постоянную |
|
|
||
функцию, то указывают число интервалов, в течение которых функция постоянна. Например, функция, показанная на рис. 8.1, г,
имеет четыре интервала постоянства.
Ограничения на управления вызваны в большинстве задач ограниченностью энергетических ресурсов системы. Фазовые координаты ограничиваются чаще всего из соображений безопасности, прочности и т. п. Например, угол и скорость поворота руля самолета ограничиваются из соображений прочности конструкции и допустимой перегрузки экипажа, а ускорение поворота руля определяется предельным вращающим моментом рулевой установки.
Ограничения на фазовые координаты будем записывать, как и для управлений, в виде неравенств типа (8.1)
N j (y) = N j ( y1,..., yn ) 0 |
, |
(8.5) |
|||
где |
|
|
|
|
|
yk = |
d k −1 y |
; |
k =1, ..., n , |
|
|
dt k −1
или в виде условий типа (8.3)
195
y Г(y) , |
(8.6) |
где ( y) – область, ограниченная гиперповерхностью |
|
N j (y) = 0 ( j =1, ..., n) . |
|
Фазовые координаты, удовлетворяющие условиям |
(8.5) или |
(8.6), называют допустимыми. |
|
Наиболее важным моментом при создании оптимальных систем
является задание критерия оптимальности. Критерий |
Q |
должен |
представлять собой величину, зависящую от функции управления. Основной задачей при разработке оптимальной системы является обеспечение предельно достижимого значения критерия. Например, при разработке систем, оптимальных по быстродействию, где к системе предъявляется требование наибыстрейшего перехода из одного положения в другое, в качестве критерия оптимальности можно взять время переходного процесса. В этом случае, естественно, критерий должен минимизироваться. Примером задачи, где критерий оптимальности должен достигать максимума, может быть расчет программы изменения тяги двигателей ракеты, когда при заданном количестве топлива требуется пролететь наибольшее расстояние.
Таким образом, для оптимальной системы необходимо
Q[u, y, t] = optimum |
при u Ω , y Г . |
(8.7) |
Условие (8.7) показывает, что критерий
Q
зависит от выходной
координаты системы, управления и времени, а задачей оптимального управления является отыскание допустимого управления u Ω(u) ,
доставляющего оптимум критерию на фазовые координаты y Г(y) .
Q
при соблюдении ограничений
Заметим, что значение
изменения функций |
y(t) |
во |
критерия Q определяется законом времени. Такие величины, значения
которых зависят от функций, называют функционалами. Математические методы отыскания функции, доставляющих экстремальное значение функционалу, рассматриваются в вариационном исчислении. Функции y(t) , u(t) , для которых
выполняется условие (8.7), называют экстремалями.
Таким образом, критерий оптимальности представляет собой функционал Q[y(t), u(t)] , а задача оптимального управления
196

заключается в ограничений u
нахождении
Ω(u) и y
экстремалей
Г(y) .
y(t)
,
u(t)
при соблюдении
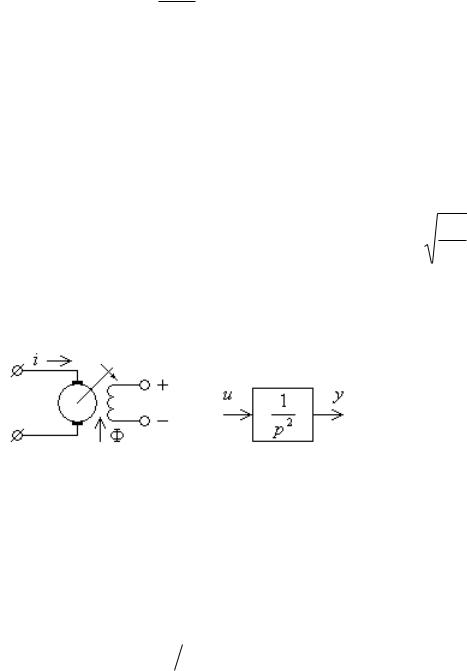
а |
б |
Рис. 8.2
Наиболее часто функционал задается в виде интеграла
T |
|
Q = G [u(t), y(t)]dt . |
|
0 |
|
Для задачи о максимальном быстродействии |
G |
Q = min u(t) обращается в требование Q = min . |
|
определенного
(8.8)
1, требование
Наиболее является задача
распространенной в оптимальном управлении
определения оптимальных процессов |
u(t) |
и |
соответственно
условиях |
y(0) |
управления |
u(t) |
y(t) в функции времени при заданных граничных
и |
y(T ). Определение оптимальных процессов |
и последующая их реализация возможны в системах
двух типов. В разомкнутой системе (рис. 8.2, а) управляющее устройство УУ по заданным граничным условиям реализует требуемый закон управления. При этом текущие фазовые координаты не участвуют в формировании управления. В замкнутой системе в УУ
(рис. 8.2, |
б) вводятся текущие фазовые координаты x = y0 − y , где |
y0 = y0 (t) |
– заданный закон управления. Управляющее воздействие |
при этом зависит только от фазовых координат, т.е. u(t) = u[x(t)] .
(8.9)
Конечной целью при разработке системы является установление закона (8.9) для построения замкнутой системы оптимального управления, т.е. синтез УУ. При этом находят оптимальные процессы u(t) и x(t) , а затем, исключая время, получают зависимость u(x) , из
которой находят структуру и параметры УУ.
197
8.2. Примеры постановки задач оптимального управления
8.2.1. Управление двигателем постоянного тока. Допустим,
что имеется возможность управлять током якоря двигателя постоянного тока с независимым возбуждением (рис. 8.3, а). Примем, что магнитный поток Ф неизменен. В этом случае угол α поворота двигателя связан с током через дифференциальное уравнение равновесия моментов на валу
|
d |
2 |
α |
|
icФ = J |
|
|
||
|
|
2 |
||
|
dt |
|||
|
|
|
||
+
M
c
,
(8.10)
где i – ток якоря – управляющее воздействие; с – коэффициент; Ф – магнитный поток; J – момент инерции якоря и нагрузки, приведенный к валу двигателя; M c – момент сопротивления; α –
угол поворота вала двигателя – управляемая координата; t – реальное время.
Для простоты дальнейших выкладок примем, что моментом сопротивления можно пренебречь, т. е. M c = 0 . Кроме того, вместо
реального времени можно ввести относительное время
этом случае уравнение (8.10) примет вид
τ = t |
cФ |
|
J |
||
|
. В
d |
2 |
α / dτ |
2 |
|
|
=
i
.
(8.11)
а |
б |
|
|
Рис. 8.3 |
|
Учитывая принятые обозначения (у – управляемая координата, и |
||
– управляющее воздействие), |
введем замену i = u , |
α = y . С учетом |
такой замены окончательно запишем уравнение управляемого объекта (рис. 8.3, б)
d 2 y dτ2 = u . |
(8.12) |
198

Можно сформулировать несколько задач оптимального управления двигателем, которые будут отличаться критериями оптимальности и видом ограничений.
Оптимальное быстродействие. В этом случае критерием оптимальности является время переходного процесса Т, т.е. функционал имеет вид
T Q = dt = T
0
.
(8.13)
Задача 8.1. Найти максимальные процессы управляющего воздействия u(t) и скорости y(t), удовлетворяющие уравнению (8.12) и
доставляющие минимум функционалу (8.13), при условиях: |
|
|||
1. на управление наложено ограничение вида (8.4), т. е. |
u 1; |
|||
2. требуется отработать угол α0 , т. е. |
|
|||
T |
|
|
|
|
y(t)dt = 0 ; |
(8.14) |
|||
0 |
|
|
|
|
3. граничные условия по скорости вращения вала имеют вид |
||||
y(0) = ω |
0 |
; |
|
|
|
|
|
||
y(T ) = ω |
|
|
||
|
. |
|
||
|
|
T |
|
|
Для простоты выкладок применим, что начальная и конечная |
||||
скорости вращения вала равны нулю, т. е. |
|
|||
y(0) = y(T ) = 0 . |
(8.15) |
|||
Принимая в качестве цели управления отработку |
угла α0 , |
|||
следует указывать и граничные условия по координате у. Примем для всех примеров управления двигателем, что y(0) = −α0 ; y(T ) = 0 , т. е.
y |
изменяется на величину |
α0 |
, заканчивая движение в точке |
y(T ) = y(T ) = 0 . |
|
|
|
Задача 8.2. В этой задаче ограничения накладываются на нагрев двигателя или на расход энергии, т. е. задана величина интеграла
T
u 2 (t)dt .
0
199

Итак, найти оптимальные процессы
удовлетворяющие уравнению (8.12) и доставляющие при условии, что заданы значения интегралов
u(t) |
и |
y(t) , |
минимум (8.13),
T |
|
T |
2 |
|
|
y(t)dt = α0 |
; |
u |
(t)dt = q0 |
||
|
|||||
0 |
|
0 |
|
|
и граничные условия по скорости нулевые.
(8.16)
Оптимальная производительность. В этом случае критерием
оптимальности является угол |
α |
поворота вала за определенное время |
Т, т. е. функционал имеет |
|
|
Q
T =
0
y(t)dt
.
(8.17)
Задача 8.3. Найти оптимальные процессы |
u(t) , |
y(t) , |
удовлетворяющие уравнению (8.12) и максимизирующие (8.17), при условии, что на управление наложено ограничение вида (8.4), т. е. u 1, и граничные условия по скорости нулевые.
Если задан предельный расход энергии, а величина и не ограничивается, то можно сформулировать другую задачу на оптимальную производительность.
Задача 8.4. Найти оптимальные
удовлетворяющие уравнению (8.12) и (8.17), при условии, что задано значение
процессы |
u(t |
доставляющие
)
иy(t) ,
максимум
T |
2 |
|
|
u |
(t)dt = q0 |
||
|
|||
0 |
|
|
и граничные условия по скорости нулевые.
Оптимальная экономичность. В этом случае критерием оптимальности является расход энергии за определенное время. Функционал имеет вид
T |
|
Q = u 2 (t)dt . |
(8.18) |
0 |
|
В данном случае имеется в виду расход энергии на нагрев двигателя.
200

Задача 8.5. Найти оптимальные процессы
u(t)
и
y(t)
,
удовлетворяющие уравнению (8.12) и минимизирующие (8.18), при условии, что задано
T y(t)dt = α0 0
и граничные условия по скорости нулевые.
Можно, варьируя условия, поставить еще ряд задач, например, когда одновременно наложены ограничения на управление и расход энергии. Однако ограничимся сформулированными задачами по управлению двигателем, так как они вполне отражают встречающиеся на практике требования к оптимальному управлению.
|
8.2.2. Оптимальная по быстродействию встреча |
||||||
движущихся объектов. Пусть |
объект A совершает |
равномерное |
|||||
прямолинейное движение в соответствии с уравнением |
(8.19) |
||||||
|
y |
A |
= a + bt |
, |
|||
|
|
|
|
|
|
||
где |
y A – координата объекта A ; а, b – постоянные; t – время. |
|
, |
||||
|
По той же прямой в пространстве за ним движется объект |
B |
|||||
|
|
|
|
|
|
|
|
изменение координаты yB которого описывается уравнением второго порядка
|
|
d |
2 |
y |
|
|
|
dy |
|
|
|
|
|
|
|
|
|
|
|
|||
|
T |
|
B |
+ |
B |
= u |
|
|
|
|
|
|
|
(8.20) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
2 |
|
|
dt |
|
|
|
|
|
|
|
|||||||
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
с начальными условиями |
B |
|
|
|
|
|
|
|
B |
|
|
|
|
, |
|
|
|
|
|
|
(8.21) |
|
|
y |
(0) |
|
= y |
(0) = 0 |
|
|
|
|
|
|
|||||||||||
где Т – постоянная |
|
|
|
|
, |
характеризующая его |
||||||||||||||||
времени |
|
|
объекта |
B |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
инерционные свойства. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На управление наложено ограничение вида (8.4), т. е. |
u 1. |
|||||||||||||||||||||
Ставится задача так изменять управление |
|
u(t) , чтобы за |
||||||||||||||||||||
минимальное время положение и скорости объектов A и B в |
||||||||||||||||||||||
пространстве совпали. |
Изменение координат |
y |
A |
и |
y |
B |
в функции |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
времени показано на рис. 8.4, а.
На практике подобная задача возникает, например, при заправке в воздухе самолетов, когда заправщик движется с постоянной скоростью и на параллельный курс к нему пристраивается заправляемый самолет. Управляющим воздействием при этом является тяга P двигателя самолета, заходящего на заправку.
201
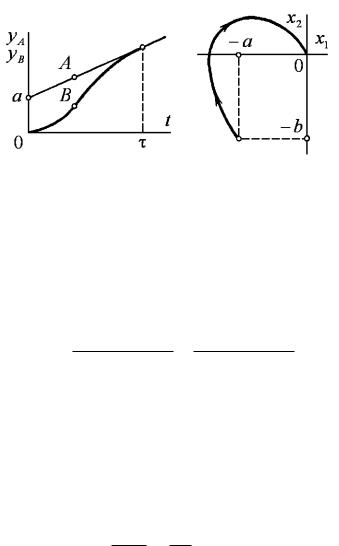
а |
б |
Рис. 8.4
Предельные значения тяги
Pmin
и |
Pmax |
положительны, поэтому
для того, чтобы записать ограничения на управление в виде (8.4),
вместо |
P |
будем рассматривать управление |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2P |
|
|
P |
|
+ P |
|
|
|
|
u = |
|
|
− |
max |
min |
. |
||
|
|
P |
− P |
P |
|
− P |
||||
|
|
|
|
|
|
|
||||
|
|
|
max |
min |
|
|
max |
min |
|
|
Для решения задачи удобно ввести в рассмотрение |
||||||||||
рассогласование между координатами объектов |
|
|||||||||
|
|
|
|
x = y |
B |
− y |
A . |
|
(8.22) |
|
|
|
|
|
|
|
|
|
|||
Подставляя
yB
из (8.22), а
y A
из (8.19) в уравнение (8.20),
получим
|
d |
2 |
x |
|
dx |
|
T |
|
|
+ |
|||
|
|
2 |
dt |
|||
|
dt |
|
||||
|
|
|
|
|||
= u
−
b
.
(8.23)
Начальные условия для уравнения (8.23) находим по известному закону движения объекта из уравнения связи (8.22) с учетом нулевых начальных условий для движения объекта B:
x(0) = yB (0) − yA (0) |
= −a; |
(8.24) |
|
x(0) = yB (0) − yA (0) |
= −b. |
||
|
Если теперь ввести фазовую плоскость для переменной x, обозначив x = x1 , x = x2 , то задачу управления движением объекта В можно сформулировать как задачу наибыстрейшего перевода точки
на фазовой плоскости из исходного положения ( |
x |
= −a |
, |
x |
2 |
= −b |
) в |
1 |
|
|
|
начало координат (рис. 8.4, б).
Задача 8.6. Найти оптимальные процессы u(t) и x(t) , удовлетворяющие уравнению (8.23) и доставляющие минимум
202
