
9. КАЧЕСТВО ПРОЦЕССОВ УПРАВЛЕНИЯ И ПРЯМЫЕ МЕТОДЫ ЕГО ИССЛЕДОВАНИЯ
9.1. Понятие о качестве САУ
Устойчивость системы автоматического управления – необходимое, но далеко не достаточное условие рациональности ее применения. Очевидно, что устойчивая система при отработке различных воздействий может оказаться недостаточно точной, переходные процессы управления в ней могут затухать очень медленно – недостаточное быстродействие, не будет обеспечена требуемая плавность изменения выходной величины. Следовательно, система не сможет достаточно хорошо осуществить автоматическое управление.
Комплекс требований, определяющих поведение системы в установившемся и переходном процессах отработки заданного воздействия, объединяется понятием качества процесса управления (качества системы). Требования этого комплекса выдвигаются практикой, т. е. конкретным применением данной системы.
При исследовании систем автоматического регулирования приходится решать задачу обеспечения требуемых показателей качества переходного процесса: быстродействия, колебательности, перерегулирования, характеризующих точность и плавность протекания процесса. Будем, как и в предыдущих главах, предполагать, что система автоматического управления описывается системой линейных дифференциальных уравнений с постоянными коэффициентами.
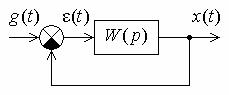
Рис. 9.1
При изменении воздействия g(t) на входе системы (рис. 9.1) выходную величину x(t) можно записать
x(t) xс(t) xв(t), |
(9.1) |
186
где x(t) – решение дифференциального уравнения, описывающего систему; xс(t) – общее решение, соответствующее однородному дифференциальному уравнению; xв(t) – вынужденная составляющая переходного процесса, обусловленная законом изменения g(t).
Если уравнение не имеет кратных корней, то
n p t
xс Cie i ,
i 1
где Ci – постоянная интегрирования, величину которой определяют параметры системы и начальные условия; pi – корни характеристического уравнения замкнутой системы D(p) 0.
Из (9.1) видно, что качество переходного процесса можно оценить по его составляющим xс(t) и xв(t). В этом смысле различают две группы показателей: первая группа – показатели качества переходного процесса xс(t); вторая – показатели, характеризующие вынужденную (установившуюся) составляющую xв(t), по которой определяют точность системы.
Показатели качества, определяемые непосредственно по кривой переходного процесса, называют прямыми оценками качества. Кривая переходного процесса может быть получена теоретически или экспериментально. Обычно рассматривают поведение системы при следующих типовых воздействиях: единичной ступенчатой функции 1(t), импульсной функции δ(t) и гармонической функции sinωt. Часто получение прямых оценок качества бывает связано с большими трудностями, так как расчет переходного процесса в системах высокого порядка сложен и эксперимент не всегда осуществим. Поэтому используют косвенные оценки качества, полученные иным путем, не требующим нахождения кривой переходного процесса.
Существующие косвенные методы оценки качества регулирования в линейных непрерывных системах можно разделить на три группы: корневые, интегральные и частотные.
187
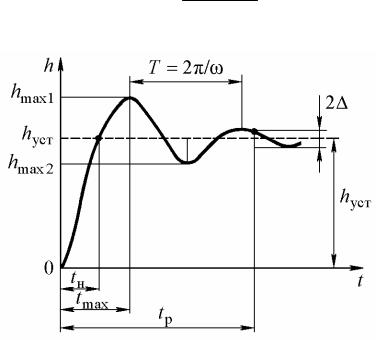
9.2. Оценка качества переходного процесса при воздействии ступенчатой функции
Переходный процесс в системе является ее реакций на внешнее воздействие, которое в общем случае может быть сложной функцией времени. Чаще всего прямые оценки качества получают по кривой переходной характеристики h(t), т. е. при воздействии единичной ступенчатой функции:
1 |
при |
t 0 |
g(t) 1(t) |
при |
(9.2) |
0 |
t 0 |
|
и нулевых начальных условиях. |
|
|
Эта характеристика может |
быть |
построена для выходной |
величины x(t)или для отклонения εс(t) (рис. 9.2 и 9.3). Выходная величина системы x(t) в этих условиях равна переходной функции замкнутой системы
1 |
Ф(p) |
|
|
|||
x(t) h(t) L |
|
|
|
, |
(9.3) |
|
p |
||||||
|
|
|
|
|
||
где Ф(p) – передаточная функция замкнутой системы
Ф(p) W(p) . 1 W(p)
Рис. 9.2
188
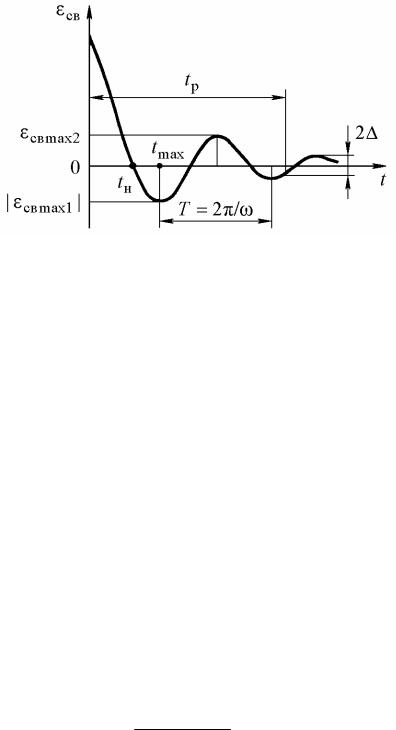
Рис. 9.3
К прямым оценкам качества относят:
1. Установившееся значение выходной величины, определяющее статическую точность системы
h |
lim h(t) h( ) lim |
p |
Ф(p) |
Ф(0). |
|
|
|||||
уст |
t |
p 0 |
|
p |
|
2. Время регулирования tр – минимальное время, по истечении |
|||||
которого регулируемая |
величина будет оставаться близкой |
||||
к установившемуся значению с заданной точностью
|h(t) hуст | или | св(t)| при t tр,
где – постоянная величина, значение которой нужно оговаривать. Задается величина в процентах от установившегося значения выходной величины hуст, обычно 5%.
3. Перерегулирование σ – максимальное отклонение переходной характеристики от установившегося значения выходной величины, выраженное в относительных единицах или процентах
σ hmax hуст 100%,
hуст
где hmax – значение первого максимума, или
|
|
св(t) |
max |
100% |
|
св(t) |
max |
100%. |
||
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||
|
|
hуст |
|
св(0) |
|
|
||||
Допустимое значение перерегулирования в каждом конкретном случае будет подсказано опытом эксплуатации системы, обычно σ 10 30%. Иногда перерегулирование недопустимо совсем.
189
4.Частоту колебаний ω 2π/T , где T – период колебаний для колебательных переходных характеристик.
5.Число колебаний n, которое имеет переходная характеристика h(t) или εсв(t) за время регулирования tр.
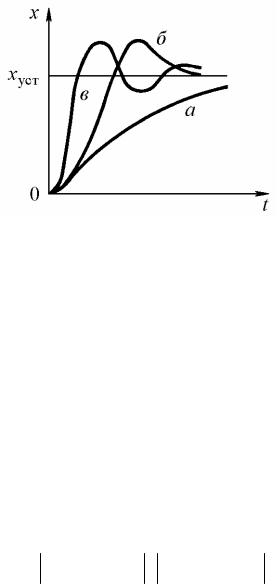
Рис. 9.4
При проектировании систем чаще всего допускают n 1 2, а иногда и до 3…4, но в некоторых случаях колебания в системе недопустимы.
6.Время достижения первого максимума tmax .
7.Время нарастания переходного процесса tн – абсцисса первой точки пересечения кривой переходной характеристики h(t) с уровнем установившегося значения hуст или кривой отклонения εсв(t) с осью
абсцисс.
8. Декремент затухания χ, равный отношению модулей двух смежных перерегулирований
χ hmax1 hуст /hmax2 hуст .
Перечисленные показатели качества могут быть дополнены другими, но это обусловлено спецификой конкретной системы.
Определение приведенных выше прямых оценок качества переходного процесса проиллюстрировано на рис. 9.2 и 9.3.
Переходные процессы, возникающие в системах при скачкообразных воздействиях, принято делить на три группы: монотонные, апериодические и колебательные. У монотонных процессов первая производная выходной величины x(t) не меняет знак (кривая а на рис. 9.4), у апериодических знак производной x(t)
190
меняется не более |
одного раза (кривая |
б на рис. 9.4), |
а у колебательных – |
первая производная x(t) |
меняет свой знак |
периодически (теоретически бесконечное число раз) (кривая в на рис. 9.4).
Нужно отметить, что в настоящее время при бурном развитии вычислительной техники трудности, связанные с расчетом переходных процессов и выбором возможных вариаций параметров системы, существенно уменьшаются, поэтому роль прямых оценок качества при проектировании систем автоматического регулирования возрастает.
Проведем анализ переходных процессов в системах низкого порядка.
Система первого порядка. Свойства системы первого порядка, поведение которой описывает передаточная функция вида
W(p) k , Tp 1
определяют два параметра: коэффициент передачи k и постоянная времени T.
Переходный процесс на выходе такой системы при g(t) 1(t)
t
h(t) k(1 e T )
представляет собой экспоненту, скорость затухания которой зависит от T, а установившееся значение (статика) для выходной переменной соответствует выражению
hуст k.
Время регулирования такого монотонного переходного процесса при 0,05 определяется из выражения
tр
e T 0,05,
следовательно равно
tр T ln0,05 2,996T 3T .
Таким образом, коэффициент передачи k определяет установившееся значение переходных процессов в системе первого порядка, а постоянная времени T – их длительность.
Система второго порядка. Рассмотрим теперь свойства системы второго порядка с передаточной функцией
191

k
W(p) T2 p2 2 Tp 1.
Переходные процессы в ней зависят от трех параметров: коэффициента передачи k, постоянной времени T и коэффициента демпфирования ξ.
Коэффициент передачи k, как и в случае систем первого порядка, определяет установившееся значение переходных процессов hуст k. Однако вид и длительность процессов зависят не только от
постоянной времени, но и от коэффициента демпфирования.
В такой системе переходный процесс при 1 ξ имеет монотонный характер; при 0 ξ 1 – колебательный характер. При ξ 0 переходный процесс представляет собой незатухающие колебания; при ξ 0 – расходящиеся колебания.
Переходный процесс на выходе такой системы при g(t) 1(t)
и 0 ξ 1: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
α |
2 |
β |
2 |
|
|
αt |
|
|||||||
h(t) k 1 |
|
|
|
|
|
e |
sin(βt 0) , |
||||||||||
|
|
|
β |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
. |
||||||||
|
|
|
|
|
|
|
/T, |
|
|
1 ξ2 |
|||||||
α ξ/T, |
β |
1 ξ2 |
0 arctg |
||||||||||||||
|
|
|
|
||||||||||||||
ξ
При 1 ξ передаточную функцию системы можно представить в виде
k
W(p) , (T1p 1)(T2 p 1)
где
T1,2 |
|
T |
. |
|||
|
|
|
|
|
||
|
|
2 1 |
||||
|
|
|
||||
Тогда переходные процессы: при ξ 1
|
|
T |
|
t |
|
T |
|
t |
|
|
|
|
|
T |
|
T |
|
|
|||||
h(t) k |
1 |
1 |
e |
1 |
|
2 |
e |
2 |
|
; |
|
T1 T2 |
T1 T2 |
||||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
192
при ξ 1
|
|
|
t |
|
t |
|
|
||
h(t) k |
|
T |
|
. |
|||||
|
|
e |
|
||||||
|
|
|
|
||||||
1 1 |
|
|
|
|
|||||
|
|
|
T |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Для определения качества рассмотренных систем, а также систем более высокого порядка можно использовать метод стандартных переходных функций, рассмотренный в параграфе 12.4.
Пример 9.1. Какой должна быть величина коэффициента передачи пропорционального регулятора в системе, замкнутой единичной обратной связью с передаточной функцией разомкнутой части
W(p) |
k |
, |
|
(Tp 1)p |
|||
|
|
чтобы переходный процесс не имел перерегулирования?
Решение. Найдем передаточную функцию замкнутой системы:
Ф(p) |
W(p) |
|
k |
. |
|
|
|||
1 W(p) |
|
Tp2 p k |
||
Приведем полученное выражение к стандартной передаточной функции динамического звена второго порядка
1
Ф0(p) T02 p2 2T0ξ0 p 1.
Известно, что для такого звена при ξ0 1 переходные процессы имеют монотонный характер.
Тогда
T |
|
T |
; ξ |
0 |
|
|
1 |
|
. |
|
|
|||||
|
|
k |
|
|
|
|
|
|||||||||
0 |
|
|
|
|
|
2 |
Tk |
|||||||||
Следовательно, при |
|
1 |
|
|
1 |
или при k |
0,25 |
переходные |
||||||||
|
|
|
|
|
|
|
||||||||||
2 |
|
Tk |
|
|
|
|
|
|
|
|
|
T |
||||
процессы не будут иметь перерегулирование.
При k 0,25/T характеристическое уравнение системы принимает следующий вид
Tp2 p k T2 p2 Tp 0,25 (Tp 0,5)2 0.
Этому случаю соответствуют два кратных корня p 0,5/T .
1,2
193
9.3. Оценка качества регулирования при гармонических воздействиях
При гармонических воздействиях качество системы принято оценивать по амплитудно-фазовой, амплитудно-частотной, фазочастотной и логарифмическим частотным характеристикам.
Для оценки качества переходного процесса системы можно использовать следующие величины: показатель колебательности M , резонансная (собственная) частота ωр, полоса пропускания системы
ω0, частота среза ωср, запасы устойчивости по модулю и по фазе.
а |
б |
Рис. 9.5
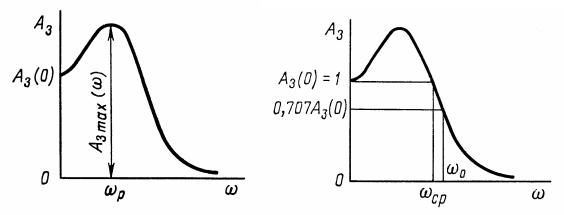
Показатель колебательности M – это отношение максимального значения амплитудно-частотной характеристики Aзmax (ω) замкнутой системы к ее значению при ω 0 (рис. 9.5, а)
M Aзmax(ω)/Aз(0), |
(9.4) |
при Aз(0) 1, M Aзmax(ω).
Показатель колебательности характеризует склонность системы к колебаниям. Чем выше M , тем менее качественна система при прочих равных условиях.
Частоту ωр, при которой амплитудно-частотная характеристика
замкнутой системы имеет максимум, называют резонансной частотой системы (рис. 9.5, а), т. е. на этой частоте гармонические колебания проходят через систему с наибольшим усилением.
194
Полоса пропускания системы (рис. 9.5, б) – это интервал частот от ω 0 до ω0, при которой выполняется условие
|
Aз(ω0) 0,707Aз(0), |
(9.5) |
или при Aз(0) 1 |
величина Aз(ω0) 0,707. Полоса пропускания не |
|
должна быть слишком широкой, иначе система будет воспроизводить высокочастотные помехи.
Частота среза ωср – частота, при которой амплитудно-частотная
характеристика системы принимает значение, равное 1, т. е. Aз( ср) 1. Эта частота косвенно характеризует длительность
переходного процесса. Чем меньше частота среза, тем хуже быстродействие системы
tр (1 2)2 / ср. |
(9.6) |
Если переходной процесс имеет одно-два колебания, то время достижения переходной характеристикой первого максимума
tmax / ср. |
(9.7) |
Склонность системы к колебаниям характеризуется величинами ее запасов устойчивости по модулю и по фазе, определение которых дано в предыдущей главе. Запасы устойчивости рассчитывают по амплитудно-фазовым и логарифмическим частотным характеристикам. В хорошо демпфированных системах запас устойчивости по амплитуде колеблется в пределах от 6 до 20 дБ, а запас по фазе – от 30 до 60°.
Так как рассмотренные выше показатели косвенно определяют быстродействие, перерегулирование и т. п., то они могут быть использованы и для расчета систем, находящихся под воздействием непериодических возмущений.
9.4.Оценка качества регулирования в установившемся режиме
9.4.1.Коэффициенты ошибок. Рассмотрим показатели качества, характеризующие вынужденную составляющую ошибки
εв(t) системы. Если на входе системы (см. рис. 9.1) действует сигнал
g(t), то установившаяся ошибка регулирования системы εв(t) g(t) xв(t), где xв(t) – вынужденная составляющая регулируемой величины (9.1).
195
