
временные характеристики, системы (переходную функцию, функцию веса и др.).
Исходной системой называют систему, у которой все параметры равны расчетным значениям и не имеют вариаций. Этой системе соответствует так называемое основное движение.
Варьированной системой называют такую систему, у которой произошли вариации параметров. Движение ее называют варьированным движением.
Дополнительным движением называют разность между варьированным и основным движением.
Пусть исходная система описывается совокупностью нелинейных уравнений первого порядка
|
dxi |
F (x |
, , x |
,α , , α |
m |
), i 1, 2, , n. |
(9.18) |
||
|
|
||||||||
|
dt |
i |
1 |
n |
1 |
|
|
||
Рассмотрим |
|
|
мгновенные |
|
вариации |
параметров |
|||
αj, j 1, 2, , m, |
так |
что параметры приняли значения j j. |
|||||||
Если изменения параметров не вызывают изменения порядка дифференциального уравнения, то варьированное движение будет описываться совокупностью уравнений
~ |
~ ~ |
~ |
|
|
|
|
|
|
dxi |
|
|
|
|
||
|
|
Fi(x1, , xn,α1 |
α1, ,αm αm), |
i 1, 2, |
, n. |
(9.19) |
|
|
dt |
||||||
Для дополнительного движения можно записать |
|
|
|||||
|
|
|
|
~ |
|
|
(9.20) |
|
|
|
|
xi(t) xi(t) xi(t). |
|
|
|
При условии дифференцируемости ~xi(t) и xi(t) по параметрам αj, j 1, 2, , m дополнительное движение можно разложить в ряд
Тейлора.
Для малых вариаций параметров допустимо ограничиться линейными членами разложения. Тогда получим уравнения первого приближения для дополнительного движения
m |
x |
|
|
m |
|
|
i |
|
αj uij αj . |
(9.21) |
|
xi(t, α1, ,αm) |
α |
|
|
||
j 1 |
|
j 0 |
j 1 |
|
|
Частные производные, находящиеся в скобках, должны быть равны их значениям при αj 0.
Таким образом, первое приближение для дополнительного движения может быть найдено при известных функциях
206

чувствительности. Заметим, что использование функций чувствительности удобнее для нахождения дополнительного движения по сравнению с прямой формулой (9.20), так как она во многих случаях может дать большие ошибки вследствие необходимости вычитать две близкие величины.
При значительных вариациях αj может оказаться
необходимым использование второго приближения с удерживанием в ряде Тейлора, кроме линейных, а также квадратичных членов.
Дифференцирование |
исходных |
уравнений |
(9.22) |
по |
j |
|||||||||||||||||||
приводит к так называемым уравнениям чувствительности |
|
|
||||||||||||||||||||||
|
|
|
dx |
|
d |
x |
|
|
|
duij |
|
n F |
|
|
|
F |
|
|
|
|
||||
|
|
|
|
i |
|
|
|
i |
|
|
|
|
|
|
i |
u |
|
|
i |
. |
(9.22) |
|||
|
|
|
dt |
|
|
dt |
|
x |
|
kj |
|
|||||||||||||
|
j |
|
|
dt |
|
|
|
|
|
k |
|
|
|
j |
|
|
||||||||
|
|
|
|
|
|
|
|
j |
|
|
|
k 1 |
|
|
|
|
|
|
|
|||||
Решение этих уравнений дает функции чувствительности |
uij . |
|||||||||||||||||||||||
Однако уравнения (9.22) оказываются сложными и решение их затруднительно. Более целесообразен путь структурного построения модели, используемой для нахождения функций чувствительности.
Обратимся теперь к линейным системам. Не снижая общности рассуждений, можно рассматривать случай изменения одного j-го параметра.
Для нахождения функций чувствительности и дополнительного движения удобно использовать передаточные функции системы. Пусть, например, регулируемая величина x(t,αj) связана
с задающим воздействием зависимостью
x(t, αj) L 1[Ф(p,αj)]G(p), |
(9.23) |
где G(p) – изображение задающего воздействия g(t).
Функция чувствительности может быть получена из (9.23) дифференцированием по параметру αj :
uj(t)
x(t,αj)
αj
Здесь введена функции
|
|
Ф(p, αj) |
|
|
L 1 |
|
G(p) L 1[Sj(p)G(p)]. |
||
αj |
||||
|
|
|
||
|
|
|
|
функция чувствительности передаточной
Ф(p, αj) |
|
|||
Sj(p) |
|
, |
(9.24) |
|
αj |
||||
|
|
|
||
|
|
0 |
|
|
207
которая определяет первое приближение дополнительной передаточной функции, равной разности варьируемой и исходной передаточных функций при вариации параметра αj
~
Ф(p,αj) Ф(p,αj) Ф(p,αj) Sj(p) αj.
Эти зависимости справедливы в том случае, когда вариация параметра αj не меняет порядка характеристического уравнения
системы.
Может также использоваться так называемая логарифмическая функция чувствительности
Ф |
|
Ф(p, αj) αj |
|
lnФ(p,αj) |
|
αj |
Sj(p). (9.25) |
||
Sα j |
(p) |
|
|
|
|
|
|
|
|
|
|
lnαj |
Ф(p, αj) |
||||||
|
|
Ф(p,α j) αj |
|
|
|
||||
Найдем дополнительную передаточную функцию для случая, когда исходная передаточная функция может быть представлена в виде отношения двух полиномов:
Ф(p,αj) Sj(p) αj |
Ф(p,α |
j |
) |
αj |
M(p, α |
j |
) |
α j |
||||
αj |
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
αj D(p,αj) |
||||||
|
[ M(p) Ф(p, αj) D(p)], |
|
(9.26) |
|||||||||
|
|
|||||||||||
|
D(p, αj) |
|
|
|
|
|
|
|
|
|
||
где M(p) и D(p) – вариации полиномов числителя и знаменателя передаточной функции Ф(p,αj).
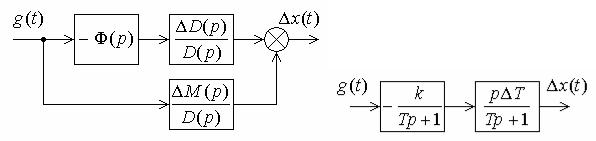
Формула (9.26) позволяет составить структурную схему модели чувствительности в виде, изображенном на рис. 9.7, а. Эта схема может быть использована для нахождения функции дополнительного движения x(t) или функции чувствительности u(t) x(t)/ αj
расчетным путем или моделированием на ЭВМ.
а |
б |
Рис. 9.7
208

Пример 9.5. Передаточная функция системы соответствует апериодическому звену первого порядка
Ф(p) k .
Tp 1
Необходимо определить функции чувствительности при входном сигнале g(t 1(t)) и построить модель чувствительности при вариации постоянной времени T.
Решение. Сигнал на выходе системы будет
t
x(t) k(1 e T ) 1(t).
Функции чувствительности по коэффициенту передачи и постоянной времени:
|
t |
|
t |
|
|
t |
|
|
|
|
|
|
|||||
uxk(t) (1 e T ) 1(t); uxT (t) k |
|
e |
T 1(t). |
|||||
T2 |
||||||||
Дополнительное движение этого звена |
|
|
|
|
||||
|
|
|
|
|
||||
x(t) uxk(t) k uxT (t) T
|
|
|
t |
|
|
|
|
|
|
t |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
(1 e T ) k k |
|
|
|
e |
T T. |
|
|
|||||||||||
|
T2 |
|
|
||||||||||||||||
Логарифмические функции чувствительности |
|
|
|||||||||||||||||
|
SkФ(p) |
1 |
|
|
|
Tp 1 |
k 1; |
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Tp 1 |
|
k |
|
|
|
|
|
|
|
|
||||||
STФ(p) |
kp |
|
Tp 1 |
T |
Tp |
. |
|||||||||||||
(Tp 1)2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
k |
|
|
|
|
Tp 1 |
||||||||
Для модели чувствительности при вариации постоянной |
|||||||||||||||||||
времени T находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D(p) Tp 1; |
D(p) p T; |
|
M(p) k; |
M(p) 0. |
|||||||||||||||
При этом получаем модель чувствительности, представленную на рис. 9.7, б.
Контрольные вопросы
1.Что относится к прямым оценкам качества?
2.Что такое время регулирования, величина перерегулирования переходного процесса?
209
3.Какие переходные процессы называются апериодическими, монотонными?
4.Что характеризует показатель колебательности?
5.Что такое частота среза системы?
6.Как определить порядок астатизма замкнутой системы?
7.Дайте определение статической системе.
8.Дайте определение системе с астатизмом ν-го порядка?
9.К чему приводит увеличение числа интегрирующих звеньев?
10.Как определяются функции чувствительности?
210
