
9. ОПТИМАЛЬНАЯ ФИЛЬТРАЦИЯ
9.1. Синтез линейных систем с минимальной средней квадратической ошибкой
9.1.1. Постановка задачи
автоматического управления с
синтеза. Рассмотрим передаточной функцией
систему
W ( p) ,
служащую для усиления и преобразования управляющего полезного
сигнала |
G(t) |
при наличии случайной помехи |
F (t) . Это |
преобразование в общем случае производится в соответствии с
некоторым заданным оператором (алгоритмом преобразования) |
H ( p) |
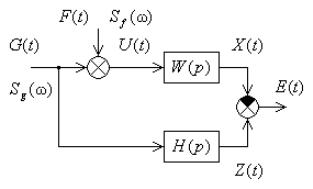
(рис. 9.1). |
|
Рис. 9.1
В общем случае система должна возможно более точно воспроизводить на своем выходе не само управляющее воздействие
G(t) , а некоторую функцию от управляющего воздействия |
|
Z (t) = H ( p)G(t) . |
(9.1) |
В системах, находящихся под воздействием случайного (или регулярного) полезного сигнала и случайной помехи, возникает задача отделения полезного сигнала от помехи и подавления (фильтрации) последней. Эту задачу называют задачей фильтрации
или сглаживания.
Введение преобразующего оператора H ( p) обобщает задачу не только на обычные следящие системы, у которых Z (t) = G(t) (т. е.
H ( p)
=
1
, но и
на другие классы систем, выполняющие различные
преобразования управляющего сигнала. В зависимости от вида оператора H ( p) задача фильтрации сочетается с задачей
222
воспроизведения (если
H ( p) = const
), упреждения (предсказания),
или
H ( p)
экстраполяции (если H ( p) = e pτ ), интегрирования (если = 1/ p ), дифференцирования (если H ( p) = p ) и др. В общем
случае преобразующий оператор H ( p) может быть произвольным.
Идеальное преобразование полезного сигнала в соответствии с (9.1) невозможно из-за динамических ошибок системы, а также из-за наличия возмущающих воздействий (помех). Поэтому выходной
сигнал (регулируемая величина) |
X (t) |
будет отличаться от |
воспроизводимого сигнала
E(t
Z (t) ) = Z
. Разность
(t) − X (t)
(9.2)
называют случайной ошибкой системы.
Синтез систем при случайных воздействиях заключается в определении динамических характеристик системы, наилучшим образом обеспечивающих выполнение некоторого статистического критерия оптимальности. Существуют различные статистические критерии оптимальности. Однако наиболее часто за статистический критерий оптимальности принимают критерий минимума средней квадратической ошибки
|
|
= |
|
2 |
с.к |
|
|||
|
|
|
|
|
|
T |
2 |
|
|
= |
lim (1/ 2T ) |
(t)dt |
|||
|
|||||
|
T → |
−T |
|
|
|
|
|
|
|
||
,
(9.3)
где ε(t) – любая реализация случайной ошибки.
В этом случае задача синтеза состоит в том, чтобы найти такую физически реализуемую оптимальную передаточную функцию замкнутой системы Wопт ( p) , при которой было бы минимальным
среднее значение квадрата ошибки
ε |
2 |
|
= {Z (t) − X (t)}2
=
min
.
(9.4)
Согласно критерию средней квадратической ошибки, оценка точности системы производится в зависимости от среднего, а не мгновенного значения ошибки, что не всегда является достаточным, например тогда, когда требуется, чтобы ошибка не выходила за заданные пределы. Применение этого критерия может оказаться нерациональным и в тех случаях, когда требования к величине ошибки в разные моменты времени неодинаковы.
Однако, несмотря на то, что этот критерий, впрочем, как и всякий другой косвенный критерий, не является универсальным, он благодаря своей простоте получил широкое практическое
223
применение.
При воздействии на систему не коррелированных между собой стационарного случайного сигнала и помехи среднее значение
квадрата ошибки состоит из двух составляющих: ε |
2 |
2 |
|
= εg + ε |
|
Если бы к системе было приложено только одно |
||
воздействие, либо полезный сигнал G(t) , либо |
|
помеха |
2 f
.
внешнее
F (t) , то
теоретически соответствующим выбором параметров передаточной функции (полосы пропускания) системы можно было бы обеспечить любую точность систем. Однако при одновременном действии полезного сигнала и помехи точность системы не может быть любой.
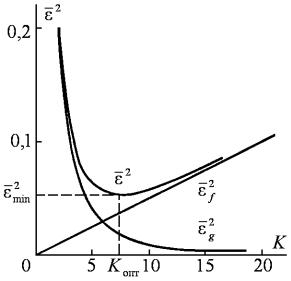
Это наглядно видно из рис. 9.2, где изображены графики
зависимости составляющих ошибки |
2 |
и |
2 |
g |
f |
||
коэффициента усиления разомкнутой системы |
K |
. |
|
|
|
|
|
от величины
Рис. 9.2
Для лучшего воспроизведения управляющего сигнала
G(t)
, т. е.
уменьшения составляющей ошибки ε g2 система должна иметь
возможно больший коэффициент усиления. Однако, для того чтобы лучше подавлять помеху F (t) , т. е. уменьшить составляющую
ошибки
ε2 f
система, наоборот, должна иметь возможно меньший
коэффициент |
K |
. Поэтому, когда на систему действуют одновременно |
|
|
|
|
|
полезный сигнал и помеха, |
существует некоторое компромиссное |
||
(оптимальное) решение и |
соответствующие ему оптимальные |
||
224
параметры системы (в данном случае Kопт ), при которых среднее
значение квадрата ошибки будет минимальным, меньше которого его, при заданных статистических характеристиках управляющего сигнала и помехи, никаким изменением параметров сделать нельзя.
Взависимости от вида графиков спектральной плотности управляющего сигнала и помехи способы решения задачи синтеза при случайных воздействиях могут быть различны.
Впростейшем случае, когда спектры частот полезного сигнала
S |
g |
(ω) |
|
|
и помехи
S |
f |
(ω) |
|
|
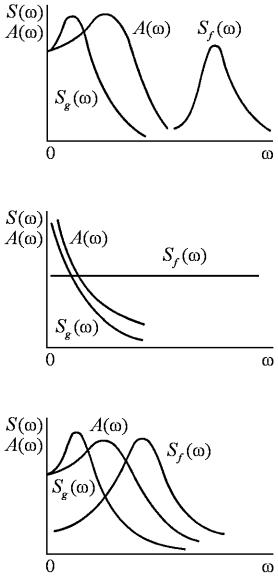
не налагаются друг на друга (рис. 9.3, а),
амплитудно-частотную A(ω) =| W ( jω) | выбирают
характеристику замкнутой системы достаточно широкой для обеспечения
требуемой точности воспроизведения управляющего сигнала и в то же время достаточно узкой для того, чтобы система меньше реагировала на помеху.
Если управляющий сигнал имеет спектр частот, очень быстро убывающий с возрастанием частоты, а спектр помех близок к белому шуму (рис. 9.3, б), то в этом случае форма амплитудно-частотной
характеристики |
A(ω) =| W ( jω) | |
разомкнутой системы должна |
выбираться |
при |
низких |
сконцентрирована |
основная |
|
возможно |
более |
близкой |
управляющего сигнала |
S g (ω) |
|
частотах, |
где |
| W ( jω) | 1 |
и |
|
|
энергия |
управляющего |
сигнала, |
||
к |
форме |
спектральной |
плотности |
||
, |
а затем должна быстро убывать, |
по |
|||
возможности следуя за убывающей характеристикой
S g
(ω)
.
Наиболее общим является случай, когда спектры частот полезного сигнала и помехи накладываются друг на друга и имеют произвольную форму (рис. 9.3, в). В этом случае при синтезе систем со случайными воздействиями различают два вида задач:
1.Синтез при заданной структуре системы управления, когда добиваются минимума средней квадратической ошибки, выбирая оптимальные параметры корректирующих звеньев системы на основании известных статистических характеристик полезного сигнала и помехи.
2.Синтез при произвольной структуре системы управления, когда по заданным статистическим характеристикам полезного сигнала и помехи определяют оптимальную структуру и параметры системы, при которых обеспечивается минимум средней квадратической ошибки.
225
а
б
в
Рис. 9.3
9.1.2. Синтез при заданной структуре системы. В этом случае задача синтеза формулируется следующим образом. Заданы: статистические характеристики полезного сигнала и помехи,
например спектральные плотности |
S g (ω) |
и |
S f (ω) ; структура |
системы и ее передаточная функция W ( p) =W ( p, β1, β2 , , β
– параметры системы.
Требуется найти оптимальные параметры β1опт , β2опт , , βnопт при которых обеспечивается минимум
n ) |
где βi |
системы
средней
квадратической ошибки.
Эта задача решается следующим образом: зная спектральные
226
плотности
определяют
пользуясь
S g (ω) , |
S f (ω) |
спектральную
табличными
и передаточную функцию системы, плотность ошибки Sε (ω) , а затем, интегралами, находят аналитическое
выражение среднего значения квадрата ошибки получается зависящим от параметров системы:
|
2 |
|
,
которое
|
2 |
|
Дифференцируя (9.5)
= F
по
(β |
, β |
1 |
|
βi , |
|
2 |
, |
|
где
,
i
βn ) .
=1, 2, ,
n
,
(9.5)
и приравнивая
нулю частные производные
ε |
2 |
|
|
|
|
= 0 |
, |
||
β |
||||
|
|
|||
|
i |
|
|
|
находят n уравнений, из которых параметры системы β1опт , β2опт , , βnопт
определяют оптимальные , обеспечивающие минимум
средней квадратической ошибки.
Как правило, большинство параметров системы изменять трудно либо невозможно, так как они определяются заданными техническими или конструктивными соображениями. Поэтому обычно варьируют два-три параметра, например постоянные времени корректирующих звеньев, коэффициент усиления разомкнутой системы и др. Если число переменных n невелико, то отыскание экстремума функции не вызывает затруднений. При большом числе n , когда явное выражение среднего значения квадрата ошибки через параметры системы определить затруднительно, либо оно слишком громоздко, используют приближенные методы отыскания минимума выражения (9.5) путем числового задания интересующих параметров и построения соответствующих графиков.
Параметры системы, выбранные по критерию минимума средней квадратической ошибки, оценивают затем исходя из возможности их технической реализации и допустимых динамических показателей системы (времени регулирования, наличия и величины перерегулирования и т. д.).
Заметим, что указанная выше методика выбора оптимальных параметров системы может применяться и при одновременном воздействии на систему регулярных и случайных сигналов.
9.1.3. Синтез при произвольной структуре системы. Эта задача впервые была поставлена и решена А. Н. Колмогоровым и
227

Н. Винером.
Пусть на систему действуют полезный сигнал
G(t)
и помеха
F (t)
, которые приложены к одному и тому же входу (см. рис. 9.1) и
являются стационарными случайными процессами с равными нулю средними значениями. Если полезный сигнал и помеха приложены к разным входам, то методом эквивалентных преобразований их всегда можно привести к одному входу.
Таким образом, суммарный сигнал на входе системы будет равен
U (t) = G(t) + F (t) .
Выходной сигнал системы X (t) связан с входным сигналом U (t) уравнением
X (t) = W ( p)U (t) = W ( p)[G(t) + F (t)],
где W ( p) – передаточная функция замкнутой системы.
Допустим, что система должна воспроизводить некоторую функцию от управляющего сигнала.
Z (t) = H ( p)G(t) .
Ошибка воспроизведения равна
E(t) = Z (t) − X (t) .
Задача синтеза в случае произвольной структуры линейной системы состоит в том, чтобы при известных статистических характеристиках полезного сигнала и помехи найти такую физически реализуемую оптимальную передаточную функцию замкнутой системы Wопт ( p) при которой среднее значение квадрата
суммарной ошибки было бы минимально, т. е.
ε |
2 |
2 |
= min . |
(9.6) |
|
= {Z (t) − X (t)} |
Wопт
Рассмотрим задачу синтеза оптимальной передаточной функции ( p) , считая, что нам заданы спектральные плотности полезного
сигнала
S |
g |
(ω) |
|
|
и помехи
S f
(ω)
, а
также преобразующий оператор
(алгоритм преобразования) H ( p) . Решение проведем для
упрощенного, но часто встречающегося случая, когда полезный сигнал и помеха некоррелированы.
Выражение для любой реализации случайной суммарной ошибки можно записать следующим образом:
ε(t) = z(t) − x(t) = H ( p)g (t) −W ( p)u(t) =
=[H ( p)] −W ( p)]g(t) −W ( p) f (t) .
228

Выражение для спектральной плотности ошибки
Sε (ω) =| H ( jω) −W ( jω) |2 Sg (ω)+ | W ( jω) |2 S f (ω),
а среднее значение квадрата ошибки
|
2 |
|
1 |
+ |
2 |
|
|
|
|
2 |
|
|
ε |
= |
{| H ( jω) −W ( jω) | |
Sg (ω)+ | W ( jω) | |
S f (ω)}d |
||||||||
|
||||||||||||
|
|
|
|
|||||||||
|
|
|
2π |
|
|
|
|
|
|
|
||
|
|
|
|
− |
|
|
|
|
|
|
|
|
Для |
|
минимизации ошибки |
ε |
2 |
необходимо |
|||||||
|
|
|||||||||||
соответствующую частотную передаточную функцию
Wопт ( jω) .
ω . (9.7)
выбрать
системы
Основная трудность в минимизации выражения (9.7) связана с учетом условий физической осуществимости передаточной функции системы Wопт ( p) . Найдем сначала Wопт ( p) без учета этого условия, а
затем на основе полученного решения построим лучшую физически реализуемых систем.
Записав частотные передаточные функции H ( jω) и |
W ( jω) |
|||
виде |
|
|
|
|
H ( jω) = H (ω)e |
jψ(ω) |
= H (ω) cos ψ(ω) + jH (ω) sin ψ(ω) ; |
||
|
|
|||
W ( jω) = A(ω)e |
j (ω) |
= A(ω) cos (ω) + jA(ω) sin (ω) |
, |
|
|
||||
из
в
вычислим
| H ( jω) −W ( jω) |2 = H 2 (ω) + A2 (ω) − 2H (ω) A(ω) cos[ψ(ω) − (ω)].
Тогда (9.7) принимает вид
|
1 |
+ |
|
|
ε 2 = |
{{H 2 |
(ω) + A2 (ω) − 2H (ω) A(ω) cos[ψ(ω) − (ω)]}Sg (ω) + |
||
|
||||
|
2π |
|
||
|
|
− |
|
|
2 |
(ω)S |
+ A |
|
|
f |
(ω)}dω
.
(9.8)
Из (9.8) необходимо найти такие значения
A(ω)
и (ω) , при
которых выполнялось бы условие |
ε |
2 |
= min . Это типичная |
|
вариационная задача, решаемая, например, с помощью уравнений Эйлера.
Учитывая, что |
H (ω) , |
A(ω) , S g (ω) и |
S f |
(ω) |
положительны при |
||
любом значении |
ω , |
для |
минимизации |
ε |
2 |
необходимо, чтобы |
|
|
|||||||
отрицательный член |
2H (ω) A(ω) cos[ ψ(ω) − (ω)] |
был наименьшим, |
|||||
т. е. чтобы |
|
|
|
|
|
|
|
|
|
|
ψ(ω) = (ω) . |
|
|
|
(9.9) |
Тогда (9.8) примет вид
229

|
2 |
|
1 |
+ |
|
2 |
|
2 |
|
|
|
|
ε |
= |
{[H |
(ω) + A |
(ω) − 2H (ω) A(ω)]S g (ω) + |
||||||||
|
||||||||||||
|
|
|
|
|||||||||
|
|
|
2π |
|
|
|
|
|
|
|
||
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
+ |
|
|
|
|
|
+ A |
(ω)S f (ω)}dω = |
Q dω |
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2π |
||
|
|
|
|
|
|
|
|
|
|
|
− |
|
Поскольку все члены в последнем подынтегральном выражении положительны, то минимум среднего значения квадрата ошибки будет при минимальном значении функции Q.
Приравнивая dQ / dA(ω) = 0 , получаем
[2 A(ω) − 2H (ω)]S |
g |
(ω) + 2 A(ω)S |
f |
|
|
откуда находим выражение для оптимальной характеристики замкнутой системы:
(ω) = 0 |
, |
амплитудно-частотной
A |
(ω) = |
|
S |
g |
(ω) |
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
опт |
S |
|
(ω) + S |
|
|||
|
g |
f |
|||||
|
|
|
|
|
|
||
Имея в виду, что Wопт ( jω) = |
A(ω)e |
j ( |
|||||
|
|
||||||
можно объединить в одно уравнение:
H (ω) . |
(9.10) |
(ω) |
|
ω) |
|
, выражения (9.9) и (9.10)
W |
( jω) = |
|
S |
g |
(ω) |
|
|
|
|
|
|||
|
|
|
|
|
||
опт |
S |
|
(ω) + S |
|
||
|
g |
f |
||||
|
|
|
|
|
||
(ω)
H (
jω)
.
(9.11)
Как следует из (9.11), единственными статистическими характеристиками полезного сигнала и помехи, необходимыми для определения оптимальной частотной передаточной функции замкнутой системы, являются их спектральные плотности.
Однако оптимальная частотная передаточная функция, определяемая (9.11), оказывается в общем случае физически нереализуемой. Это можно показать на частном простейшем примере. Пусть решается задача воспроизведения, т. е. H ( jω) = 1, и пусть
помеха представляет собой единичный белый шум, т. |
е. |
S f (ω) |
||||||
Тогда |
|
|
|
|
|
|
|
|
Wопт ( jω) = |
|
Sg (ω) |
H ( jω) = |
Sg (ω) |
|
, |
|
|
Sg (ω) + S f (ω) |
Sg (ω) +1 |
|
||||||
|
|
|
|
|
||||
и, поскольку |
Sg (ω) +1 |
– положительная величина, |
||||||
=1.
она
раскладывается на комплексные множители, один из которых всегда будет иметь полюсы в нижней полуплоскости корней. Импульсная переходная функция w(t) , найденная для такой частотной
230
передаточной функции, будет существовать и для отрицательных значений времени t 0 , т. е. до начала переходного процесса (до приложения возмущения). Это и свидетельствует о нереализуемости
( jω) .
Условием физической реализуемости является выполнение равенства w(t) = 0 при t 0 ; в этом случае Wопт ( jω) будет иметь все полюсы в верхней полуплоскости корней, а соответствующая ей передаточная функция Wопт ( p) будет иметь только левые корни.
Пример 9.1. Найти оптимальное значение
H ( jω) = 1, Sg (ω) =1/(1+ ω2 ) , S f (ω) =1.
Решение. По последней формуле получим
W (
jω)
,
если
W |
( jω) = |
1 |
|
= |
|
|
|
|
|||
опт |
|
2 + ω |
2 |
( |
2 + |
|
|
||||
|
|
|
|
|
1 |
|
jω)( |
2 − |
jω)
.
Это выражение соответствует последовательному соединению двух инерционных звеньев, одно из которых неустойчиво и в практических устройствах не может быть реализовано. Это становится особенно ясно при переходе от Wопт ( jω) к весовой
функции:
|
|
1 |
+ |
1 |
|
|
jωt |
w |
(t) = |
|
|
e |
|||
|
|
|
|||||
|
|
|
|
||||
опт |
|
2π |
2 + ω |
2 |
|
|
|
|
|
|
|
|
|||
|
|
− |
|
|
|
||
|
|
|
|
|
|
|
dω =
|
1 |
2 |
2 |
e |
−|t| |
2 |
|
.
а |
б |
Рис. 9.4
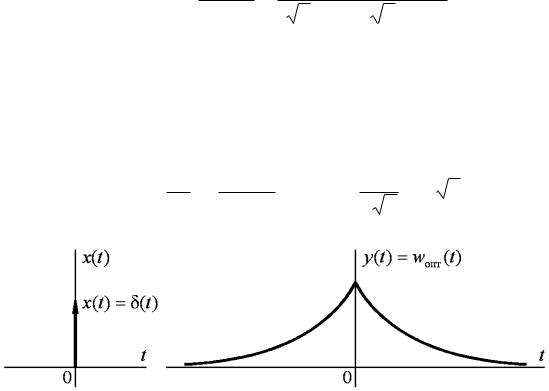
График реакции системы wопт (t) на единичный импульс δ(t)
(рис. 9.4, а) в этом случае показан на рис. 9.4, б. Как видно из графика, для реализации требуемой весовой функции необходимо,
231
