
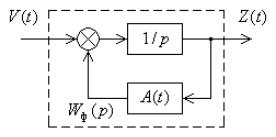
Уравнение (9.42), полученное во временной области, эквивалентно оптимальному фильтру Винера, определяемому в частотной области уравнением (9.19).
Остановимся кратко на очень существенном для фильтров Калмана – Бьюси вопросе о возможности представления случайного процесса Z (t) в виде дифференциального уравнения (9.29).
Нахождение (9.29) связано с задачей определения формирующего фильтра (стационарного или нестационарного), который при воздействии на его вход белого шума V (t) позволяет
получить на своем выходе заданный случайный процесс
Z (t)
.
Структурная схема такого формирующего фильтра в соответствии с (9.29) может быть представлена так, как показано на рис. 9.6.
Рис. 9.6
Для стационарных случайных процессов методы определения параметров формирующих фильтров разработаны хорошо. В этих случаях формирующий фильтр можно описать обыкновенным дифференциальным уравнением с постоянными коэффициентами или соответствующей передаточной функцией формирующего фильтра Wф ( p) . Особенно просто находится передаточная функция
формирующего фильтра спектральной плотности
S
в
z |
(ω |
|
)
том случае, когда выражение для стационарного случайного процесса
Z (t) имеет вид дробно-рациональной функции частоты, т. е., когда выражение для спектральной плотности может быть представлено в виде произведения двух комплексно-сопряженных множителей:
S z
Пусть на входе стационарный случайный
(ω) = S1( jω)S1(− jω) . |
(9.43) |
||
формирующего фильтра |
действует |
||
сигнал |
V (t) |
типа «белый шум», имеющий |
|
|
|
|
|
спектральную плотность Sv (ω) = L , тогда спектральная плотность сигнала на выходе формирующего фильтра
242
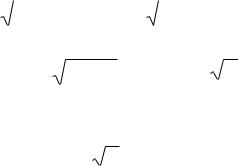
S |
z |
(ω) =| W ( jω) |2 |
S |
(ω) =W ( jω)W (− jω)S |
(ω) . |
|||
|
ф |
v |
|
ф |
ф |
v |
|
|
Учитывая (9.43), можно записать |
|
|
|
|||||
|
|
|
|
|
||||
S1( jω)S1(− jω) = [ |
Sv (ω)Wф ( jω)][ |
Sv (ω)Wф (− jω)] , |
||||||
откуда частотная передаточная функция формирующего фильтра |
||||||||
|
|
Wф ( jω) = S1( jω) / |
Sv (ω) = S1 |
( jω) / |
L . |
(9.44) |
||
Подставляя в последнее выражение
p =
jω
,
получаем
выражение для передаточной функции формирующего фильтра
W |
( p) = |
ф |
|
S |
( p) / |
L |
1 |
|
|
.
(9.45)
Зная передаточную функцию формирующего фильтра, находим дифференциальное уравнение вида (9.29), связывающее случайные процессы Z (t) и V (t) .
Если спектральная плотность S z (ω) не является дробнорациональной функцией частоты или получена экспериментально, то для нахождения формирующего фильтра ее нужно сначала аппроксимировать дробно-рациональной функцией частоты.
В заключение следует отметить, что если входные воздействия являются стационарными случайными процессами, то метод Калмана – Бьюси не имеет преимуществ перед методом синтеза оптимальных фильтров Винера. Этот метод в основном применяют для синтеза оптимальных нестационарных линейных фильтров.
Он позволяет также достаточно просто находить структуру и параметры оптимального фильтра и в том случае, когда
воспроизводимый сигнал |
Z (t) |
описывается полиномом со |
случайными коэффициентами: |
|
|
где
a |
, a |
, , a |
0 |
1 |
n |
Z (t) = a |
0 |
+ a t + |
|
1 |
–случайные
+ a |
|
t |
n |
, |
n |
|
|||
|
|
|
величины с известными
статистическими характеристиками.
Синтез оптимальных линейных фильтров Калмана – Бьюси, проведенный первоначально для помехи в виде белого шума, был в дальнейшем развит на более общие случаи, например на случай коррелированных помех, имеющих неравномерную спектральную плотность, на случай нелинейной фильтрации и др.
Заметим, наконец, что оптимальные фильтры Калмана – Бьюси, как и оптимальные фильтры Винера, позволяют решать не только задачу оптимального воспроизведения сигнала на фоне помех
243
(фильтрации), но и задачи статистического упреждения, статистического дифференцирования и т. д.
Пример 9.3. На входе линейной стационарный случайный процесс G
следящей системы действует (t) , спектральная плотность
которого
S |
|
(ω) = S |
|
2 |
|
2 |
) = 2D T |
2 |
2 |
) |
g |
g |
(0) /(1+ ω T |
|
/(1+ ω T |
|
|||||
|
|
|
g |
g g |
g |
|
||||
и случайная
помеха |
F (t) |
типа «белый шум», имеющая спектральную плотность |
S f (ω) = S f (0) = N .
Определить методом Калмана – Бьюси оптимальную передаточную функцию системы, обеспечивающую минимум
средней квадратической ошибки. |
|
||
Решение. |
|
|
|
1. Поскольку |
система |
предназначена для воспроизведения |
|
полезного сигнала |
G(t) , то |
преобразующий оператор |
H ( p) = 1, |
воспроизводимый сигнал Z (t) = G(t) и, следовательно, Sz (ω) = Sg (ω) .
Всоответствии с (9.43) представляем выражение для
спектральной плотности |
S g (ω) |
сопряженных сомножителей:
в виде произведения комплексно-
|
S |
|
(ω) = S |
(ω)S |
(−ω) = |
S |
g |
(0) |
|
S |
g |
(0) |
|
|||
|
|
|
|
|
|
|
|
|||||||||
|
g |
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
1 |
|
|
|
1 + jωT |
|
1 − jωT |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
g |
|
и находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S (ω) = |
S |
g |
(0) /(1 + |
jωT |
g |
) |
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
2. Рассматривая заданный |
стационарный случайный процесс |
||||||||||||||
G(t) |
как реакцию некоторого формирующего фильтра на |
|||||||||||||||
стационарный случайный процесс V (t) |
типа «белый шум», имеющий |
|||||||||||||||
спектральную |
|
плотность |
Sv (ω) = L , |
|
находим |
частотную |
||||||||||
передаточную функцию этого формирующего фильтра по (9.44):
W |
( jω) = |
S |
( jω) |
= |
S g (0) |
|
||
1 |
|
|
|
|
||||
ф |
|
S |
|
(ω) |
|
L |
(1 + |
|
|
|
v |
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
|
jωT |
g |
) |
|
|
.
3. Находим передаточную функцию формирующего фильтра:
W ( p) = |
G(t) |
= |
S g (0) |
|
1 |
. |
|
|
|
||||
ф |
V (t) |
|
L |
|
(1 + pTg ) |
|
|
|
|
|
4. Полученной передаточной функции формирующего фильтра
244
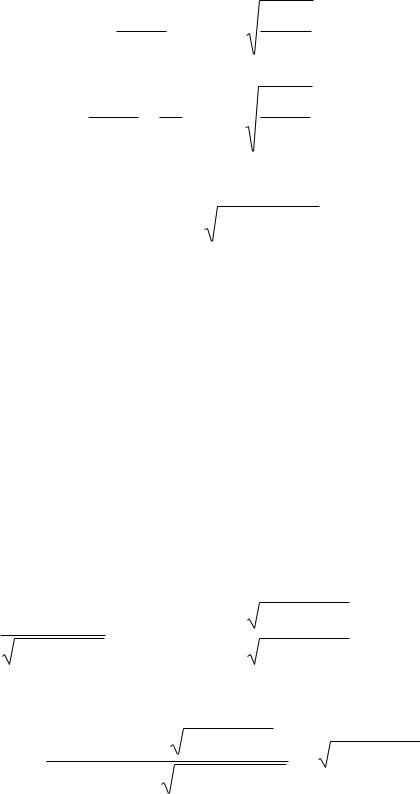
соответствует следующее связывающее случайные процессы
дифференциальное |
уравнение, |
G(t) и V (t) : |
|
T |
dG(t) |
+ G(t) = |
Sg (0) |
V (t) |
|
|
|||
g |
dt |
|
L |
|
|
|
|
или
dG(t) |
+ |
1 |
G(t) = |
|
dt |
T |
|||
|
|
|||
|
|
g |
|
S |
g |
(0) |
|
|
|
|
|
2 |
LT |
||
|
|
g |
V
(t)
.
Чтобы привести последнее дифференциальное уравнение к виду (9.29), примем, что спектральная плотность белого шума равна
S |
(ω) = L = 2D |
g |
v |
|
/ Tg
,
тогда |
S |
g |
(0) / LT 2 |
= 1 |
и окончательно |
|
|
g |
|
|
случайный процесс
где |
A = −1/ Tg . |
G
(t
) может быть представлен dG(t) / dt = AG(t) +V (t) ,
Соответствующая этому дифференциальному уравнению структурная схема формирующего фильтра показана на рис. 9.7, а.
5. Уравнение (9.37) для дисперсии ошибки в данном случае имеет вид
dr(t) / dt = L + 2 Ar (t) − r |
2 |
(t) / N |
|
|
|
||
|
|
|
|
||||
При постоянных |
значениях |
коэффициентов |
A , |
L |
и N |
||
дифференциальное |
уравнение |
является |
уравнением |
||||
разделяющимися переменными и приводится к следующему виду:
это
с
где
dr /( L + 2 Ar − r 2 / N ) − dt = 0 .
Интегрируя по общим правилам, получаем
|
|
1 |
|
− r / N + A − |
A |
2 |
+ L / N |
|
|
|
|
|
ln |
|
|
− t = ln C1 |
, |
||||
|
|
A2 + L / N |
|
A2 |
|
|||||
|
|
|
− r / N + A + |
+ L / N |
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
C |
– постоянная интегрирования. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Последнее выражение можно переписать следующим образом:
|
− r / N + A − |
A |
2 |
+ L / N |
|
ln |
|
||||
|
|
2 |
|
|
|
|
(−r / N + A + |
A |
+ L / N )C |
||
|
|
||||
= t |
A |
2 |
|
+ L / N
.
245
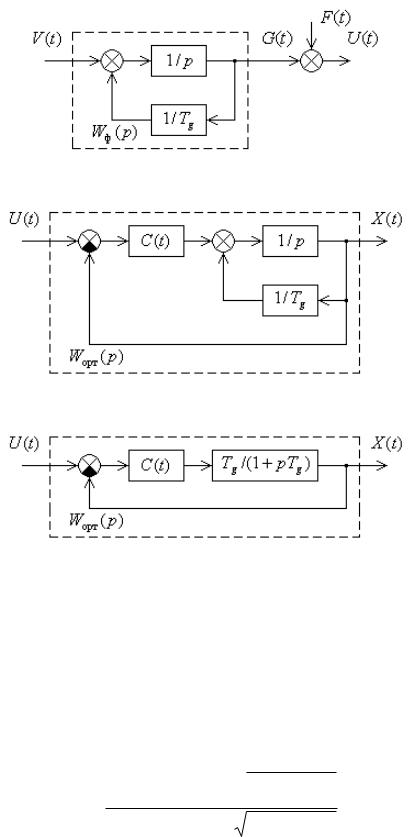
а
б
в
Рис. 9.7
Новую постоянную
условий при |
t = t0 = 0. |
В |
|
дисперсии ошибки |
|
|
|
|
r(t |
0 |
) = |
|
|
|
|
интегрирования C находят из начальных соответствии с (9.38) начальное значение
R |
gg |
(t |
0 |
, t |
0 |
) = R |
g |
(0) = D |
g |
, |
|
|
|
|
|
|
поэтому постоянная интегрирования получается равной
C= − Dg / N + A − 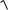
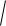 A2 + L / N .
A2 + L / N .
/N + A + 2 + L / N− Dg A
Таким образом, можно записать
246
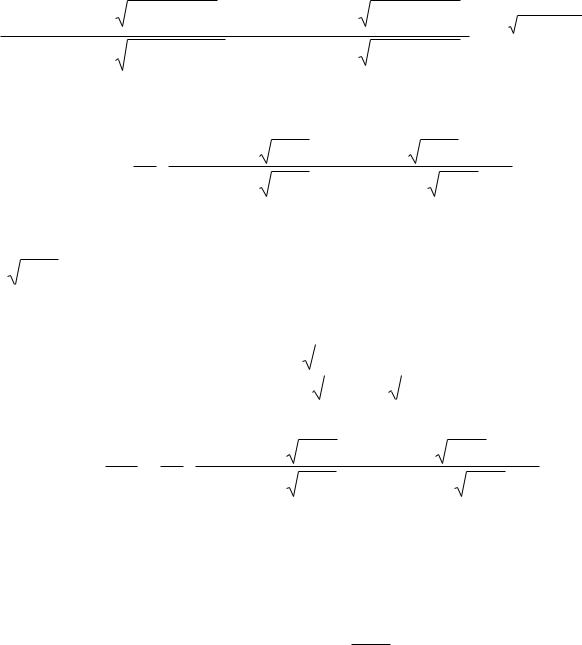
(−r / N + A − |
A |
2 |
+ L |
|
|||
(−r / N + A + |
A |
2 |
+ L |
|
Учитывая, что
/N )(−Dg /
/N )(−Dg /
L = 2Dg
N + N + / Tg ,
A + |
A |
2 |
+ L / |
|
|||
A − |
A |
2 |
+ L / |
|
|||
|
A = −1/ T |
||
|
|
|
g |
N ) N )
,
= e |
t |
|
и
A |
2 |
+L / N |
|
||
|
|
. |
производя
соответствующие преобразования, окончательно получаем
|
|
N |
|
0,5ρ(1 − |
1 + ρ ) − |
0,5ρ(1 + 1 + ρ )e |
βt |
|
|
r(t) = |
|
|
|
||||
|
Tg |
|
|
|
|
βt |
||
|
|
(1 + 0,5ρ − |
1 − ρ ) − |
(1 + 0,5ρ + 1 + ρ )e |
||||
|
|
|
||||||
где |
= Sg (0) / S f (0) |
– отношение |
спектральных |
|
||||
,(9.46)
плотностей
воспроизводимого |
|
сигнала и |
помехи |
на |
нулевой частоте; |
|||||||||||||||||
β = |
1 + ρ / Tg . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя в (9.46) |
t → , находим выражение для дисперсии |
||||||||||||||||||||
ошибки в установившемся режиме: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2Dg |
|
|
|
|
|
|||||
|
|
r = D = |
N |
|
0,5ρ(1 + 1 |
+ ρ ) |
|
= |
|
. |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
ε |
Tg |
1 + 0,5ρ − 1 + ρ |
|
|
1 + ρ +1 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
6. В соответствии с (9.139) находим функцию C(t) : |
|
|
|
|
|||||||||||||||||
|
|
r(t) |
|
1 |
|
|
0,5ρ(1 − |
1 + ρ ) − |
|
0,5ρ(1 + |
1 + ρ )e |
βt |
|
|
||||||||
|
C(t) = |
= |
|
|
|
|
. (9.47) |
|||||||||||||||
|
N |
Tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
βt |
|||||
|
|
|
|
(1 + 0,5ρ − |
1 − ρ ) − |
(1 + 0,5ρ + 1 + |
ρ )e |
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||||||
Из (9. 47) находим начальное значение коэффициента |
C (0) |
t = t0 = 0), т. е. |
|
|
|
|
|
C(0) = / 2T |
= D |
g |
/ N |
||
|
|
g |
|
|
|
и значение коэффициента |
C( ) |
в |
установившемся режиме |
||
t → ): |
|
|
|
|
|
(при
(при
C( ) = ρ / Tg (1 + 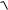
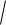 1 + ρ .
1 + ρ .
7. Дифференциальное уравнение оптимального фильтра Калмана – Бьюси в соответствии с (9.1) имеет вид
dX (t) / dt = −X (t) / Tg + C(t)[U (t) − X (t)] .
Структурная схема, соответствующая этому дифференциальному уравнению, приведена на рис. 9.7, б. Заменяя интегрирующее звено, охваченное обратной связью, инерционным звеном, можно представить структурную схему так, как показано на рис. 9.7, в.
Используя эту структурную схему и значения передаточных функций отдельных ее динамических звеньев, определяем для
247
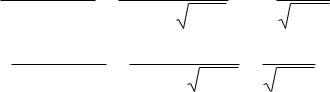
установившегося |
режима |
|
передаточную |
|
функцию |
|||||||
оптимальной системы: |
|
|
|
|
|
|
|
|
|
|
||
W |
( p) = [C( )T /(1 + pT )] /[1 + C( )T |
/(1 + pT )] = K |
||||||||||
опт |
|
g |
g |
|
g |
|
|
|
g |
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
C( )T |
|
|
ρ |
|
|
|
|
1 |
|
|
|
K = |
g |
|
= |
|
=1 − |
; |
|||||
|
+ C( )T |
|
|
|
|
|
||||||
|
1 |
g |
1 |
+ ρ + |
1 + ρ |
|
|
|
1 |
+ ρ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
T |
g |
|
|
T |
|
|
|
|
T = |
g |
|
= |
|
|
= |
|
g |
. |
|
|
|
1 + C( )T |
1 + ρ + |
1 + |
ρ |
1 |
+ |
|
|||||
|
|
g |
|
ρ |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
замкнутой
/(1 + Tp) ,
Полученное выражение для передаточной функции оптимального фильтра Калмана – Бьюси полностью совпадает с выражением для передаточной функции фильтра Винера, найденного в примерах.
Следует обратить внимание на то, что даже при стационарных случайных воздействиях в переходном режиме оптимальный фильтр Калмана – Бьюси является нестационарным, поскольку коэффициент C(t) изменяется во времени.
9.4. Контрольные вопросы
1.Как определятся средняя квадратическая ошибка?
2.Условия физической реализации фильтров.
3.В чем заключается операция факторизации?
4.В чем заключается операция расщепления?
5.Уравнение оптимального фильтра Винера
6.Что такое уравнения состояния?
7.Что такое формирующий фильтр?
8.Уравнение оптимального фильтра Калмана – Бьюси.
9.Структурная схема оптимального фильтра Калмана – Бьюси.
10.Области применения фильтров Винера и Калмана.
248
