
заменяется идеальным линейным звеном с коэффициентом передачи
k0 |
, лежащим в пределах 0 k0 k . |
|
Передаточная функция для такой разомкнутой системы равна |
k0Wл ( p) . Согласно критерию Найквиста, условие устойчивости |
|
рассматриваемой линейной системы заключается в том, что
частотная |
характеристика k0Wл ( jω) |
не должна |
охватывать точку |
(−1, j0). |
Последнее эквивалентно |
условию, |
чтобы частотная |
характеристика Wл ( jω) линейной части системы не охватывала точку
(−1/ k0 , j0). |
|
|
|
|
|
|
|
|
|
Действительно, |
граница |
устойчивости |
по |
Найквисту |
|||||
соответствует равенству |
k0Wл ( jω) = −1 или |
Wл ( jω) = −1/ k0 . |
При |
||||||
изменении величины |
k0 |
в диапазоне от 0 до |
k точка |
(−1/ k0 |
, j0) |
||||
перемещается по действительной |
оси от − |
до |
−1/ k0 . |
Поэтому |
|||||
условием устойчивости линейной системы при k0 |
= 0 k |
является |
|||||||
прохождение характеристики |
Wл ( jω) правее точки |
(−1/ k, |
j0) , |
т. е. |
|||||
непересечение ею действительной оси левее этой точки. |
|
|
|
||||||
Характеристики |
Wл ( jω) |
и |
Wл.п ( jω) |
имеют |
одинаковые |
||||
действительные части и, следовательно, пересекают действительную ось в одних и тех же точках. Поэтому сформулированное условие устойчивости линейной системы полностью относится и к характеристике Wл.п ( jω) .
Таким образом, достаточное условие устойчивости при
произвольной форме однозначной нелинейной характеристики |
z(x) |
в |
секторе [0, k] оказывается строже необходимого и достаточного
условия устойчивости в случае линейной характеристики |
z(x) |
в этом |
секторе тем, что помимо необходимости нахождения характеристики
Wл ( jω) |
правее точки |
(−1/ k, j0) |
, требует еще возможности |
проведения через эту точку линии Попова. Например, в случае
характеристики |
Wл.п ( jω) , изображенной на рис. 6.7, е сплошной |
линией, система устойчива при линейной характеристике в секторе
[0, k], но не обладает абсолютной устойчивостью. Точка |
−1/ k |
на |
действительной оси определяет критический по устойчивости
коэффициент передачи k0 |
для линейной системы, а точка с ω = ω−π – |
|
критическое значение |
k |
по условию абсолютной устойчивости в |
случае произвольной |
нелинейной характеристики z(x) . Таким |
|
158
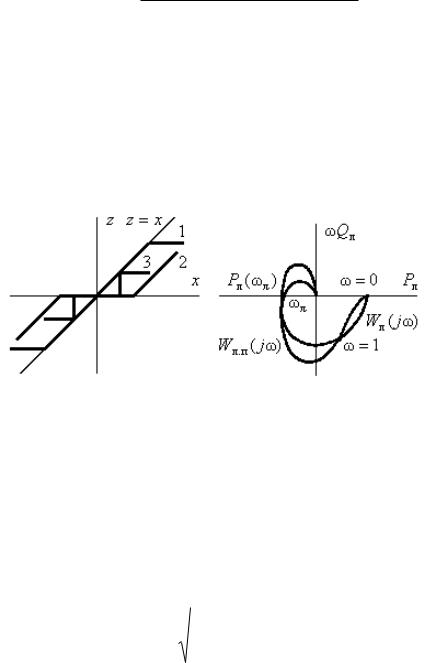
образом, при произвольной форме частотной характеристики Wл ( jω)
абсолютная устойчивость обеспечивается в меньшем угле по сравнению с устойчивостью в случае линейной системы.
Если же характеристика Wл ( jω) слева выпукла, достаточное
условие устойчивости совпадает с условием устойчивости линейной системы в том же угле (секторе).
Пример 6.6. Пусть системы
W |
( p) = |
л |
|
передаточная |
функция линейной части |
|||
|
|
k |
|
. |
(T p +1)(T |
|
|
||
p +1)(T |
p +1) |
|||
1 |
2 |
|
3 |
|
Определить значение
kпр
,
при котором система с любой
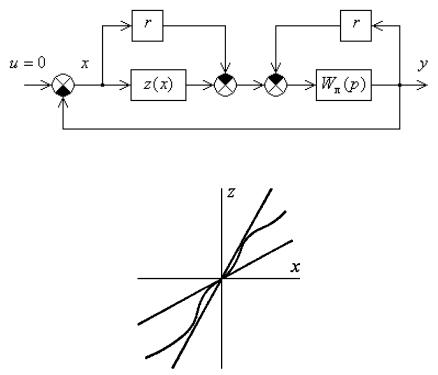
однозначной нелинейностью, лежащей в секторе [0, 1] абсолютно устойчива. В качестве нелинейности может быть, например, и ограничение (кривая 1 на рис. 6.8, а) и зона нечувствительности (кривая 2), и релейная характеристика (кривая 3), и любая иная однозначная нелинейность.
а |
б |
Рис. 6.8
Решение. Так как кривая
W |
( jω) |
л.п |
|
выпуклая (рис. 6.8, б), то для
рассматриваемой задачи может быть применен критерий Найквиста. Условием устойчивости является неравенство −Wл ( jωπ ) = −Pл (ωπ ) 1. Воспользовавшись ранее рассмотренными
результатами анализа соответствующей линейной системы, получим
ω |
π |
= |
|
T1 + T2 + T3 |
|
; |
|
T1T2T3 |
|||||||
|
|
|
|
|
|||
|
|
|
|
|
|
159
kпр = (T1 + T2 + T3 )(1/ T1 +1/ T2 +1/ T3 ) −1.
Если линейная часть нейтральна или неустойчива, критерий абсолютной устойчивости непосредственно не может быть применен. Однако в этом случае, возможно преобразовать схему так, чтобы линейная часть системы была устойчива. Taкое преобразование может быть осуществлено путем введения двух равных и противоположных но знаку пропорциональных звеньев (рис. 6.9, а).
а
б
Рис. 6.9
Коэффициент усиления пропорционального звена r выбирается так, чтобы линейная часть Wл ( p) , охваченная жесткой отрицательной
обратной связью стала устойчивой. В таком случае схема может быть представлена в виде устойчивой эквивалентной линейной части Wл.э ( p) , содержащей внутреннюю обратную связь r , и эквивалентной
нелинейной части, coдержащей внутреннюю прямую связь − r . Для этой схемы условие принадлежности нелинейной характеристики zэ (x) к сектору [0, k] соответствует принадлежности характеристики
реального нелинейного звена z(x) к сектору [r, k + r] (рис. 6,9, б). При этом
160

Wл.э ( p)
z |
э |
(x) |
|
|
= |
|
Wл ( p) |
; |
1 + rWл ( p) |
|||
= z(x) − rx . |
|
||
(6.38)
(6.39)
Если система нейтральна и имеет один нулевой корень, то добавление сколь угодно малой обратной связи r → 0 приводит задачу к условиям, когда можно применить критерий абсолютной устойчивости.
Пример 6.7. Каким условиям должна удовлетворять, нелинейная характеристика z(x) звена в системе с передаточной
функцией
W |
|
( p) = |
1 |
|
л |
|
|
||
|
( pT |
−1)(1 + pT |
) |
|
|
|
|||
|
|
1 |
2 |
|
для того, чтобы система была
абсолютно устойчива.
Решение. Найдем по формуле (6.38)
W |
( p) = |
л.э |
|
2 |
|
+ |
p T T |
||
1 |
2 |
|
1 |
|
|
p(T −T |
) −1 + r |
|
1 |
2 |
|
.
Для |
устойчивости |
||||
неравенств |
T |
T |
, |
r 1 |
. |
1 |
2 |
|
|||
Годограф Wл.э ( jω)
этой системы необходимо выполнение
системы второго порядка лежит целиком в
нижней полуплоскости. Также в нижней полуплоскости лежит и годограф преобразованной частотной характеристики Wл.э.п (ω) . Так
как в этом случае прямую Попова можно провести через любую точку отрицательной действительной оси, вплоть до начала координат, то условием абсолютной устойчивости при T1 T2 служит
0 z |
э |
/ x |
|
|
и, следовательно,
|
|
|
1 z / x . |
При |
T |
T |
система неустойчива при любой нелинейности. |
1 |
2 |
Критерий абсолютной устойчивости Попова и прямой метод Ляпунова связаны между собой. Показано, в частности, что если критерий Попова выполняется, то существует V -функция Ляпунова в форме Лурье-Постникова, имеющая во всем фазовом пространства знакоопределенную производную dV / dt со знаком, обратным знаку V . Это дает основания для предпочтения критерия Попова при практическом анализе устойчивости нелинейных систем
161
автоматического управления с одной нелинейностью, поскольку он имеет удобную частотную форму.
6.4.Контрольные вопросы
1.Приведите классификацию САУ в зависимости от наличия внешнего воздействия.
2.Что называется невозмущенным движением?
3.Что называется возмущенным движением?
4.Дайте основное определение устойчивости движения по Ляпунову.
5.В чем заключается смысл прямого метода Ляпунова?
6.Какими свойствами обладают функции Ляпунова?
7.В какой форме могут быть выбраны функции Ляпунова?
8.Приведите формулировку критерия устойчивости Попова.
9.В чем заключается преимущество критерия устойчивости Попова перед прямым методом Ляпунова.
10.Какое условие устойчивости определяется по методам Ляпунова и Попова?
162
