
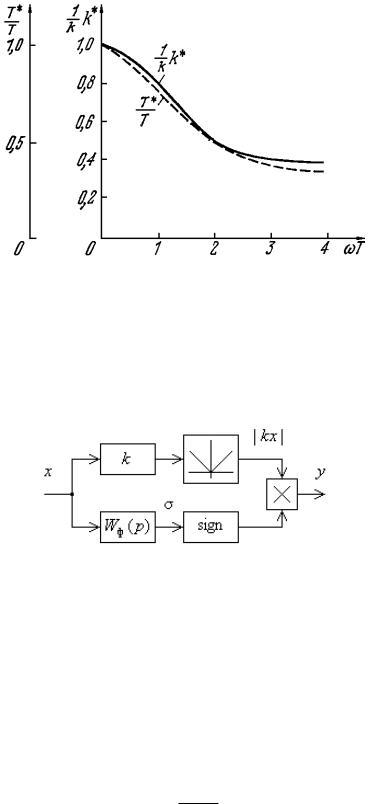
Рис. 7.17.
Пример 7.5. Нелинейный фильтр с фазовым опережением. Схема, показанная на рис. 7.18, позволяет получить фазовое опережение без изменения амплитуды.
Рис. 7.18
Она аналогична звену переменной структуры, но сложения сигналов введено умножение модуля | kx | на sign σ
вместо , где σ –
выход линейного фильтра
W |
( |
ф |
|
p)
, создающего опережение.
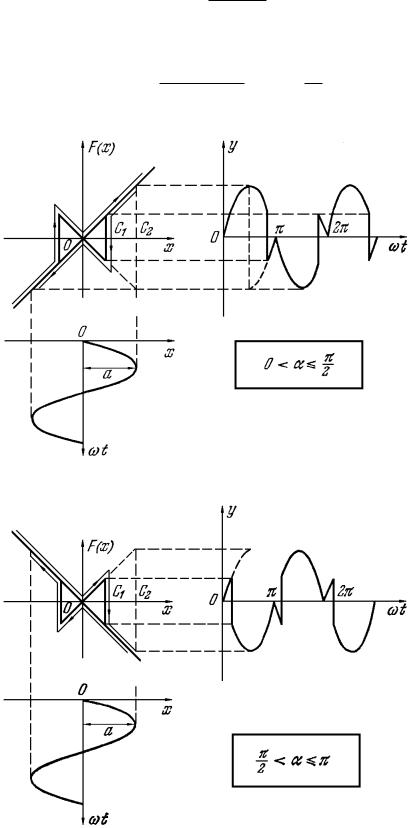
Решение. На рис. 7.19 приведены нелинейные характеристики этой схемы при разных значениях опережения α , получаемых выбором параметров схемы. Так, при 0 α π / 2 имеем
|
OC |
|
|
OC 2= a, |
1 |
||
OC |
= sin α , |
||
|
|
||
|
2 |
||
а при π / 2 α π |
|
|
|
OC 2= a, |
OC1 |
= cosα , |
|
OC2 |
|||
|
|
||
где a – амплитуда входных колебаний, причем при α = π / 2 точки C1
183
и C2 |
сливаются. Если линейная часть фильтра имеет вид |
||||||||
|
W ( p) = |
Tp +1 |
, |
|
|
||||
|
T p |
+1 |
|
|
|||||
|
|
|
|
|
|
||||
|
|
|
1 |
|
|
|
|
|
|
то опережение |
|
|
|
|
|
|
|
|
|
|
|
ωT (1 − γ) |
|
|
T |
|
|||
|
α = arctg |
|
|
|
|
, |
= |
1 |
. |
|
2 |
2 |
γ |
T |
|||||
|
|
|
|
|
|||||
|
|
1 + ω T |
|
|
|
|
|||
а
(7.29)
б
Рис. 7.19
184
Для коэффициентов гармонической линеаризации имеем формулы
причем
(0, α) и
|
2 |
π |
|
|
|
|
|
|
|
|
|
q = |
πa |
(| kx | a sin ψ) sin ψdψ, |
|
|
|
|
0 |
|
, |
(7.30) |
|
|
2 |
π |
|
||
|
|
|
|
||
q = |
|
|
|
||
πa |
(| kx | a sin ψ) cos ψdψ, |
|
|
||
|
0 |
|
|
|
|
интегралы разбиваются на два с пределами соответственно (α, π) . В результате получаем
где
α = f (ω)
q = |
k |
(π − 2α + sin 2α), |
q |
|
= |
k |
(1 − cos2α) , |
|
π |
π |
|||||||
|
||||||||
|
|
|
|
|
|
выражается формулой (7.29). Как видим, данная
нелинейная схема относится к классу псевдолинейных. Получаемое фазовое опережение
μ = arctg |
q (ω) |
|
q(ω) |
||
|
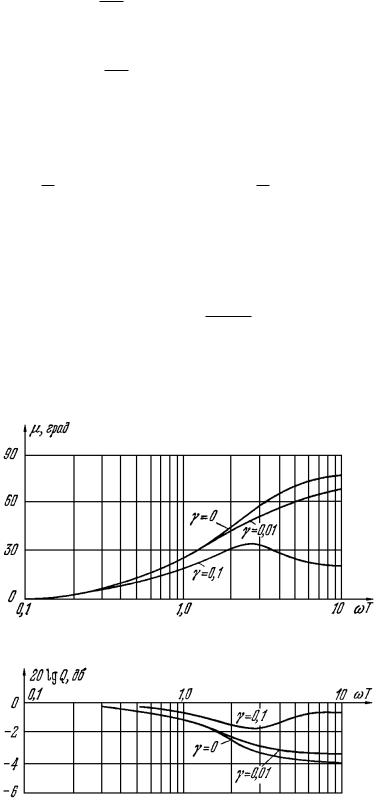
показано на рис. 7.20 при разных значениях
γ
в зависимости от
частоты
ω
, отложенной по логарифмической шкале.
а
б
Рис. 7.20.
185
При этом амплитудное искажение величиной
Q(ω)
,
определяемое
Q(ω) = |
q |
2 |
2 |
(ω) |
|
(ω) + q |
оказывается незначительным (менее 4 дБ), что вполне приемлемо для решения поставленной задачи.
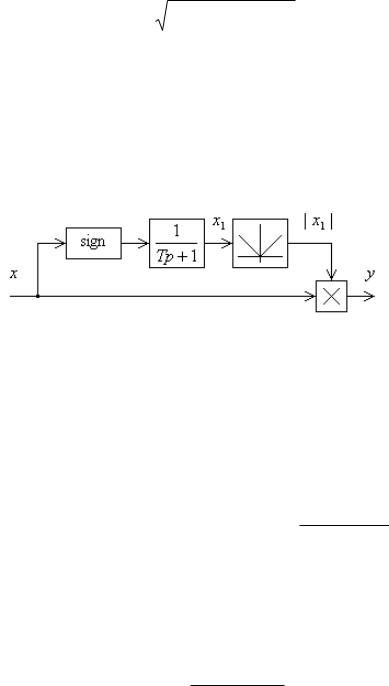
Пример 7.6. Нелинейный фильтр с амплитудным ослаблением. Схема, изображенная на рис. 7.21, позволяет получить ослабление амплитуды с ростом частоты без изменения фазы.
Рис. 7.21,
x
=
Выходной сигнал |
y =| x1 |
| x связан с |
x |
соотношением |
|
|
|
1 |
|
|
. |
|
(Tp +1)x |
= sign |
x |
|
|
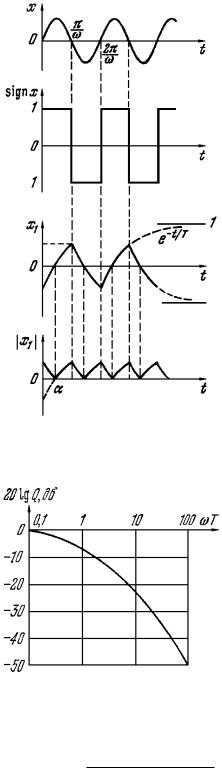
Решение. Формы колебаний входящих сюда переменных при
a sin ωt показаны на рис. 7.22, причем |
|
|
|
|
|||||
|
−1/ T |
|
−1/ T |
|
|
|
1 − e |
−π / ωT |
|
x1 = x10e |
(1 − e |
), |
x10 |
= |
|
. |
|||
|
|
1 + e |
−π / ωT |
||||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Используя формулы гармонической линеаризации (7.30), нужно |
|||||||||||
заменить в этих формулах kx на |
1 |
и разбить каждый интеграл на |
||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
два: |
(0, α) и (α, π) , где |
α – точка перемены знака x1 |
(см. рис. 7.23), |
|||||||||
определяемая выражением |
|
|
|
|
|
|
||||||
|
|
|
|
|
α = ωT ln |
|
|
|
2 |
. |
(7.31) |
|
|
|
|
|
|
|
|
|
−π / ωT |
||||
|
|
|
|
|
|
|
2 + e |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
Результат интегрирования |
|
|
|
|
|
|
||||||
|
q = 1 − |
2α |
+ |
2sin α |
(cos α − 2ωTsin α) , |
|||||||
|
|
|
|
|
|
|||||||
|
π |
π(1 + 4ω2T 2 ) |
||||||||||
|
q = − |
|
|
|
2sin α |
|
(sin α − 2ωTcos α) . |
|
||||
|
|
|
|
|
||||||||
|
|
2 2 |
) |
|
||||||||
|
|
|
π(1 + 4ω T |
|
|
|
|
|
||||
Снова отмечаем зависимость q и q только от частоты, но не от
186
амплитуды.
Рис. 7.22
Рис. 7.23
На рис. 7.23 показана амплитудная характеристика
Q(ω) = 
 q2 (ω) + q 2 (ω)
q2 (ω) + q 2 (ω)
такого псевдолинейного фильтра. Из характеристики видно эффективное подавление амплитуды колебаний. Легко проверить, что фазовое искажение при этом незначительно.
187
7.4.Системы с переменной структурой
Всистемах с переменной структурой за счет нелинейного сочетания различных линейных структур удается организовать специфическое вырожденное движение – скользящий режим, или режим перехода от движения, соответствующего одной линейной структуре, к движению, соответствующему другой линейной структуре, с помощью логического переключения связей в системе в зависимости от ее фазового состояния. Такой переход осуществляется с высокой частотой, в пределе стремящейся к бесконечности. После возникновения скользящего режима движение системы происходит вдоль границы переключения и становится независимым от параметров управляемого объекта. Если параметры объекта изменяются в процессе функционирования системы, то такие изменения не оказывают влияния на динамические свойства системы
спеременной структурой, находящейся в скользящем режиме. Следовательно, организуя в системе с переменной структурой скользящий режим, удается добиться независимости ее движения от параметрических возмущений.
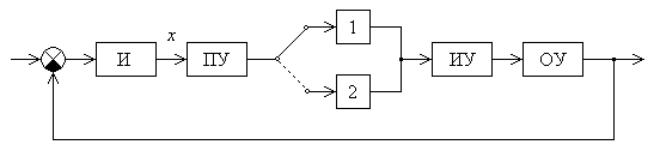
Переменная структура системы дает дополнительные возможности получения различных желаемых процессов автоматического управления и регулирования. Допустим, в системе предусмотрены две разные структуры, различающиеся звеньями 1 и 2 (рис. 7.24). Имеется логическое переключающее устройство (ПУ),
которое в зависимости от размеров и знака входной величины пары входных величин) подключает либо звено 1, либо звено 2.
x
(или
Рис. 7.24
Рассмотрим переходный процесс (без внешнего воздействия). Пусть измерительное (И) и исполнительное (ИУ) устройства идеальные и вместе с объектом управления (ОУ) описываются
188
передаточной функцией
W ( p) = k . p2
Звенья же 1 и 2 характеризуются коэффициентами усиления k1 и k2 соответственно. Тогда уравнение динамики замкнутой системы при включении звена 1 запишется в виде
d |
2 |
x |
|
|
|
||
|
|
+ k1kx = 0 |
, |
(7.32) |
|||
|
dt |
2 |
|||||
|
|
|
|
||||
|
|
|
|
|
|
||
а при включении звена 2: |
|
|
|
|
|
|
|
|
d 2 x |
+ k2kx = 0 . |
(7.33) |
||||
|
dt2 |
||||||
|
|
|
|
||||
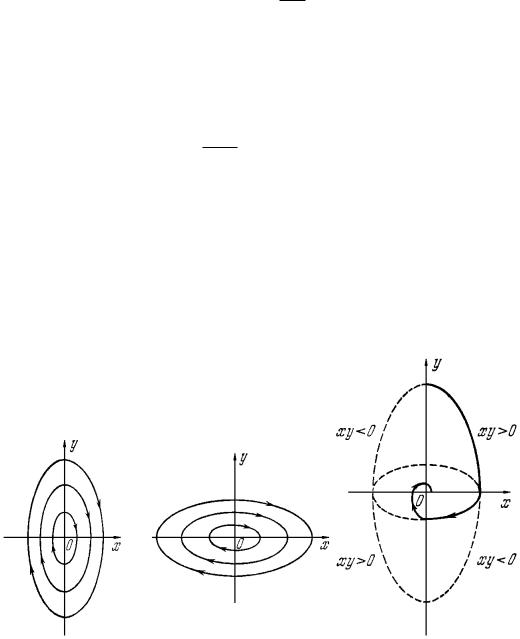
Каждое из этих уравнений является уравнением неустойчивой системы. Картины фазовых траекторий показаны на рис. 7.25, а и б соответственно.
а |
б |
|
|
|
|
Рис. 7.25 |
|
Рис. 7.26 |
|
Обозначим |
dx / dt = y . Введем следующий закон переключений. |
|||
Пусть звено 1 включается при |
xy 0 |
, а звено 2 – при |
xy 0 , т. е. |
|
имеем уравнения |
|
|
|
|
189

d 2 x |
+ k kx = 0 |
при |
xy 0; |
|
|
||||
dt2 |
1 |
|
|
|
|
|
|
||
d 2 x |
+ k2kx = 0 |
при |
xy 0. |
|
dt2 |
||||
|
|
|
В этом случае в I квадранте фазовой плоскости
( x, |
y) |
берется
дуга эллипса из рис. 7.25, а; в IV квадранте – из рис. 7.25, б; в III – снова из рис. 7.25, а и т. д. В результате, как видно по рис. 7.26, получается затухающий колебательный процесс, т. е. за счет переменности структуры система становится устойчивой.
Такой колебательный процесс не всегда приемлем. Поэтому чаще всего в системах с переменной структурой стремятся огранизовать скользящий апериодический процесс. Рассмотрим это на конкретном примере.
Пусть в той же системе (рис. 7.24) звено 1 имеет коэффициент
усиления |
k |
, а звено 2 – коэффициент усиления |
− k |
(усиление с |
1 |
1 |
переменной знака сигнала). Пусть при этом в переключающем
устройстве формируется величина |
. |
(7.34) |
|
1 |
|
||
x |
= y + cx |
|
|
Переключения в системе установим так, чтобы
d |
2 |
x |
|
|
|
|
|
|
+ k kx = 0 |
при |
x x |
||
|
|
|
|
|||
dt |
2 |
1 |
|
1 |
||
|
|
|
||||
|
|
|
|
|
||
d |
2 |
x |
|
|
|
|
|
|
− k kx = 0 |
при |
x x |
||
|
|
|
|
|||
dt |
2 |
1 |
|
1 |
||
|
|
|
||||
|
|
|
|
|
||
Тогда линиями переключения будут: ось
y = −cx ,
обозначенная на рис. 7.27 волнистой линией. Согласно (7.35) в областях, где x1x
0; (7.35)
0.
y и прямая
(7.36)
0 (т. е. в правой
полуплоскости – над линией переключения, в левой – под ней), фазовые траектории будут эллипсами. В остальных областях, где
1 |
– гиперболами. Они и показаны на рис. 7.27. |
x x 0 |
|
190
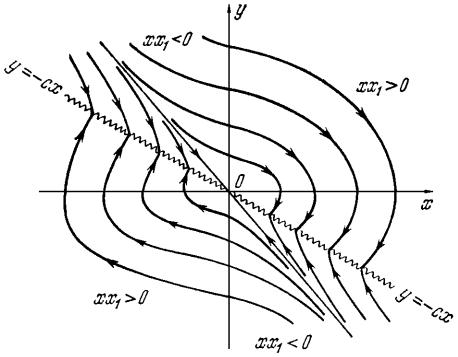
Рис. 7.27
На рисунке видно, что все фазовые траектории встречаются на линии переключения y = −cx . Видно, что на линии переключения
y = −cx фазовые траектории встречаются, упираясь в нее. Это можно расшифровать следующим образом. Пусть процесс идет по фазовой траектории 1 (рис. 7.27), Как только фазовая траектория пересечет линию переключения, вступит в свои права фазовая траектория 2, которая вернет процесс к линии переключения. Но тут встретится фазовая траектория 3 и т. д. В результате изображающая точка путем вибраций около линии переключения переместится к началу координат 0.
Такой ход процесса соответствует режиму переключения системы с большой частотой. Теоретически частота переключения бесконечна, а амплитуда вибраций, изображенных на рис. 7.27, стремится к нулю. Следовательно, теоретически изображающая точка скользит по линии переключения к началу координат – к равновесному состоянию. Процесс такого рода называется
скользящим процессом.
В данном случае линия скользящего процесса не ограничена. Поэтому при любых начальных условиях система входит в режим скользящего процесса без предварительных колебаний. Этот процесс, согласно (7.36), описывается уравнением
191

где значения
t = 0
и
dxdt + cx
x = x0
= 0, x = x0e−ct ,
определяются моментом попадания
изображающей точки на линию скользящего процесса. |
|
|
|
|
Заметим, что форма скользящего процесса зависит от параметра |
||
c |
управляющего устройства и не зависит от параметров |
k |
и k1 |
основной части системы. Это весьма важное свойство скользящего режима обусловило то, что при построении систем с переменной структурой стремятся сформировать управление таким образом, чтобы обеспечивался именно скользящий процесс.
7.5. Контрольные вопросы
1.Основные виды коррекции нелинейных систем управления.
2.Линейная коррекция нелинейных систем.
3.Что такое показатель колебательности систем?
4.Особенности нелинейной коррекции систем управления.
5.Что позволяет обеспечить псевдолинейная коррекция?
6.Структура нелинейного фильтра с фазовым опережением.
7.Структура нелинейного фильтра с амплитудным ослаблением.
8.Что такое скользящий процесс?
9.Условия реализации скользящего процесса.
10.Область применения систем с переменной структурой.
192
