

положительной ОС. Поэтому в качестве корректирующей обратной связи применяется в основном отрицательная жесткая ОС для уменьшения инерционности.
Можно показать, что при охвате такой обратной связью статического звена любого порядка, т. е. когда W0(p) k0 /Q0(p), где Q0(0) 1, происходит такое же изменение в (1 k0kос) раз коэффициента передачи k0 и всех коэффициентов полинома Q0(p).
При охвате жесткой ОС интегрирующего звена с передаточной функцией
W (p) |
k0 |
|
|
|
|||
|
|
|
|
||||
|
0 |
|
p |
|
|
||
имеем |
|
|
|
|
|||
k0 |
|
|
|
k |
|
||
W(p) |
|
|
, |
||||
p k0koc |
|
|
|||||
|
|
|
|
Tp 1 |
|||
где
k 1/kос; T 1/k0kос.
Таким образом, при охвате интегрирующего звена жесткой ОС оно превращается в статическое. Отрицательная ОС вокруг интегрирующего звена широко применяется для снижения порядка астатизма системы и соответственно для улучшения ее устойчивости в тех случаях, когда у системы оказывается излишний порядок астатизма, например в исполнительных устройствах.
В случае инерционной жесткой ОС с передаточной функцией
Wос(p) kос
Tос p 1
порядок знаменателя передаточной функции замкнутой цепи W(p) повышается на единицу по сравнению с порядком передаточной функции прямой цепи Wо(p). Если, например,
W (p) |
k0 |
|
, |
|
|
||||
0 |
T0 p 1 |
|
||
|
|
|||
то можно убедиться, что в передаточной функции замкнутой цепи W(p) в числителе появится форсирующее звено, а знаменатель будет звеном второго порядка.
W(p) |
k0(Tос p 1) |
. |
|
(T0 p 1)(Tос p 1) k0kос
249

Следовательно, инерционность отрицательной обратной связи увеличивает быстродействие звена. Инерционность положительной обратной связи, наоборот, затягивает переходной процесс.
Гибкие корректирующие обратные связи. Гибкие обратные связи содержат дифференцирующие звенья, и такие обратные связи действует только в динамике. Идеальная гибкая обратная связь (ГОС) представляет собой идеальное дифференцирующее звено
Wос(p) kос p. (11.15)
Так как сигнал обратной связи пропорционален скорости изменения сигнала, такую обратную связь называют еще обратной связью по скорости.
Для звена с передаточной функцией
W0(p) k0 Q0(p)
получаем
W(p) k0 . Q0 k0kос p
Таким образом, гибкая обратная связь, не влияя на коэффициент передачи охватываемого звена, изменяет коэффициент при p в знаменателе его передаточной функции. Можно убедиться, что для апериодического звена 1-го порядка положительная гибкая ОС уменьшает постоянную времени, а отрицательная, наоборот, увеличивает ее. При этом в отличие от отрицательной жесткой ОС применение положительной гибкой ОС позволяет повышать быстродействие без снижения коэффициента передачи звена. Для звена 2-го порядка отрицательная гибкая ОС, увеличивая величину коэффициента относительного демпфирования, является эффективным средством уменьшения колебательности рассматриваемого звена.
Для интегрирующего звена с передаточной функцией
W (p) |
k0 |
|
|
|
|
||
|
|
|
|
||||
|
0 |
|
p |
|
|
|
|
имеем |
|
|
|
|
|
||
|
k0 |
|
k |
|
|||
W(p) |
|
|
, |
||||
(1 k0koc)p |
|
||||||
|
|
p |
|||||
250
где
k k0 /(1 k0kос),
т. е. гибкая ОС изменяет коэффициент передачи, не изменяя типа звена.
Инерционность гибкой ОС сказывается на динамике охватываемого звена таким же образом, как и в случае жесткой обратной связи, т. е. при отрицательной обратной связи повышает быстродействие, а при положительной снижает его.
Благодаря простоте реализации инерционные ОС широко используются для повышения быстродействия (форсирования) переходных процессов. Особенно широкое распространение получила инерционная гибкая ОС вокруг интегрирующего звена, которая называется изодромной обратной связью (ИОС). В этом случае передаточная функция ОС имеет вид
W (p) |
kос p |
|
(11.16) |
||
|
|
|
|||
ос |
Tос p 1 |
||||
или при kос Tос Tи |
|||||
Tи p |
|
|
|
||
W (p) |
|
, |
|||
|
|||||
ос |
Tи p 1 |
|
|
||
|
|
|
|||
где Tи – постоянная времени изодромной обратной связи.
Действие такой обратной связи в переходном процессе, вызванном ступенчатым воздействием на входе, можно пояснить так. По теореме о начальном и конечном значениях оригинала из теории преобразования Лапласа известно, что стремлению оригинала по времени t к нулю соответствует стремление изображения по
комплексной переменной p к бесконечности lim x(t) lim px(p) и,
t 0 p
наоборот, стремление оригинала к бесконечности соответствует
стремлению изображения к нулю lim x(t) lim px(p). Применим
t p 0
это положение к передаточной функции изодромной обратной связи. В начале переходного процесса при t 0 скорость изменения переменных на входе и выходе звена велика, следовательно, p . Единицей в знаменателе Wос(p) можно пренебречь, т. е. принять Wос(p) kос /Tос. Поэтому в начале переходного процесса изодромная обратная связь ведет себя как жесткая обратная связь, превращая интегрирующее звено в статическое. В результате облегчаются
251
условия стабилизации САУ в целом и возникает возможность повысить быстродействие системы в начале переходного процесса.
В конце переходного процесса t , скорость изменения выходного сигнала в системе уменьшается, при этом p 0. Следовательно, Wос(p) 0 и сигнал обратной связи uос спадает до нуля. Интегрирующее звено начинает вести себя как звено без обратной связи, обеспечивая астатизм САУ в целом, т. е. устраняя установившуюся погрешность.
Системы с большим коэффициентом передачи. При проек-
тировании систем автоматического управления получили применение так называемые системы с большим коэффициентом передачи. Они обладают рядом преимуществ по сравнению с другими САУ. Например, свойства системы в основном определяются статическими и динамическими свойствами цепи обратной связи.
Рассмотрим пропорциональное звено с большим коэффициентом передачи k0, охваченное обратной связью. В этом случае имеем, что
W(p) |
k0 |
|
|
|
|
1 |
1 |
, |
(11.17) |
|
|
|
|
|
|
|
|
|
|||
1 k W |
(p) |
|
1 |
W (p) |
W (p) |
|||||
|
0 oc |
|
|
|
|
|
oc |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
k0 |
oc |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
так как k0 1.
Таким образом, с помощью практически безынерционного усилителя можно получить звено с передаточной функцией, обратной передаточной функции звена обратной связи. В этом случае свойства системы определяются характеристиками звена обратной связи.
Это дает возможность создания физически труднореализуемых передаточных функций с помощью более простых обратных им передаточных функций.
11.2. Методы повышения статической точности
Задача повышения точности работы САУ может быть решена за счет увеличения общего коэффициента передачи разомкнутой системы, повышения порядка астатизма, применения неединичной обратной связи, компенсации возмущений путем применения методов теории инвариантности.
252
11.2.1. Увеличение общего коэффициента передачи разомкнутой системы. Увеличение точности за счет повышения общего коэффициента передачи – наиболее распространенный и простой метод. Значения установившихся ошибок обратно пропорциональны общему коэффициенту передачи. Так в системе автоматического управления (см. рис. 9.1) ошибка от изменения входного воздействия
ε(t) Фε(p)g(t) |
|
1 |
|
g(t). |
1 W |
|
|||
|
(p) |
|||
Тогда значение установившейся ошибки в статической системе при g(t) 1(t)
εуст(t) С0g(t) |
1 |
g(t), |
(11.18) |
|
|||
1 k |
|
||
где k – передаточный коэффициент разомкнутой системы. Аналогично может быть записано выражение для ошибки
системы от действия возмущения f (t)
ε |
уст |
(t) С |
f (t) |
|
kf |
f (t), |
|
|
|||||
|
0 f |
|
1 k |
|||
|
|
|
|
|||
где kf – передаточный коэффициент прямой цепи от возмущения f (t) до регулируемой координаты.
Следовательно, уменьшение установившейся ошибки при постоянных значениях задающего воздействия и возмущения достигается увеличением коэффициента передачи разомкнутой системы. Однако одновременно с увеличением статической точности в большинстве случаев уменьшается запас устойчивости и при значительном увеличении k система становится неустойчивой.
Пример 11.2. Противоречие между статической точностью и устойчивостью проиллюстрировано на рис. 11.6, где сплошными линиями показаны логарифмические частотные характеристики разомкнутой системы с передаточной функцией
|
W(p) k/[(T1s 1)(T2s 1)(T3s 1)] |
(11.19) |
|
при |
k 20,T1 0,01с,T2 0,025с,T3 0,5с. |
Если |
точный |
коэффициент увеличить до k 60, то логарифмическая амплитудночастотная характеристика принимает положение, показанное пунктиром. Частота среза увеличилась, а запас устойчивости по фазе
253
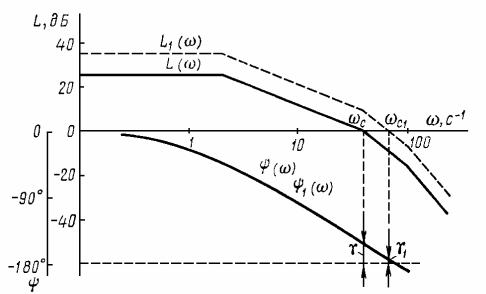
уменьшился с γ 26 до γ1 3 . Столь малый запас по фазе совершенно недопустим.
Рис. 11.6
При повышении статической точности путем увеличения передаточного коэффициента k разомкнутой системы необходимы мероприятия для обеспечения достаточного запаса устойчивости.
11.2.2. Повышение порядка астатизма системы. Другой путь повышения статической точности – обеспечение астатизма. В астатической системе младшие коэффициенты ошибки имеют следующие значения:
С0 0;С1 1/kω;С0 f 0;С1f kf /kω, (11.20)
где k – передаточный коэффициент разомкнутой системы, называемый в данном случае добротностью системы по скорости (или коэффициентом добротности по скорости).
Таким образом, в астатической системе отсутствует
установившаяся |
ошибка от |
постоянного |
задающего воздействия |
и постоянных возмущений. |
|
|
|
Астатизм |
достигается |
введением |
интегрирующего звена |
в прямую цепь системы. Для астатизма относительно возмущения интегрирующее звено должно быть введено до точки, в которой приложено возмущение (рис. 11.7, а)
254
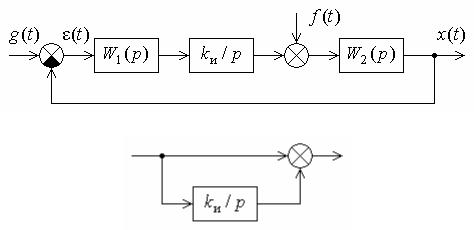
W1(p) k /(T1p 1)(T2 p 1); W2(p) 1/(T3p 1).
а
б
Рис. 11.7
Пример 11.3. Влияние интегрирующего звена на динамические свойства системы приведено на рис. 11.8, где сплошными линиями показаны логарифмические частотные характеристики системы с передаточной функцией (11.19). При введении в разомкнутую цепь этой системы интегрирующего звена характеристики принимают положение, показанное пунктиром. Фазо-частотная характеристика переместилась вниз на – 90°, а амплитудно-частотная характеристика повернулась вокруг точки а по направлению часовой стрелки.
В результате запас устойчивости по фазе уменьшился с |
γ 26 до |
|
недопустимого малого значения γ 6 |
. Система |
остается |
1 |
|
|
устойчивой, но переходной процесс будет сильно колебательным. Кроме того, уменьшилась частота среза и переходные процессы будут более продолжительными.
255
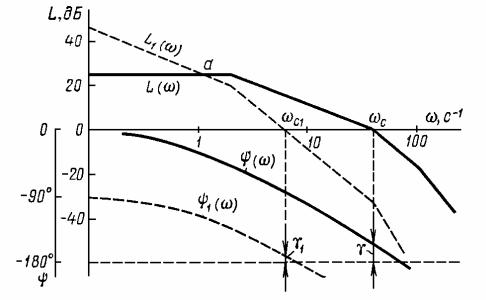
Рис. 11.8
Таким образом, при повышении статической точности путем обеспечения астатизма с помощью интегрирующего звена уменьшается быстродействие системы и могут оказаться необходимыми мероприятия для сохранения запаса устойчивости.
Значительно лучшие результаты получают при обеспечении астатизма с помощью изодромного звена, т. е. звена с передаточной функцией (рис. 11.7, б)
W |
(p) k |
и |
(Tи p 1) |
1 |
kи |
, |
(11.21) |
|
|
|
|||||||
из |
|
p |
|
|
p |
|
||
где Tи 1/kи – постоянная времени изодрома. |
|
|||||||
Если постоянная времени |
Tи |
достаточно велика, |
то запас |
|||||
устойчивости может быть сохранен неизменным. Уменьшение передаточного коэффициента разомкнутой системы должно быть скомпенсировано увеличением передаточного коэффициента другого звена (вероятнее всего, усилителя). Следует учитывать, что при большом значении Tи могут увеличиться старшие коэффициенты ошибки.
Введение в систему двух интегрирующих или изодромных
звеньев дает астатизм второго порядка. |
В этом случае C0 C1 0; |
||||
C2 1/kε; |
C0 f C1f 0; |
C2 f kf /kε, |
где kε |
– |
передаточный |
коэффициент разомкнутой |
системы, называемый |
в |
этом случае |
||
256 |
|
|
|
|
|
добротностью (или коэффициентом добротности) системы по ускорению.
В системе с астатизмом второго порядка отсутствуют установившиеся ошибки от задающего воздействия и возмущений, постоянных по величине и изменяющихся с постоянной скоростью.
Однако два последовательно соединенных интегрирующих звена делают одноконтурную систему из усилительных, апериодических и колебательных звеньев структурно неустойчивой. Следовательно, оказывается необходимым такое изменение структуры системы, при котором она становится структурно устойчивой и может быть обеспечен нужный запас устойчивости.
Возможно обеспечение астатизма и более высокого порядка. При этом из-за введения большого количества интегрирующих или изодромных звеньев и мероприятий для сохранения устойчивости и приемлемых динамических свойств, структура системы становится сложной.
11.2.3. Применение неединичной обратной связи и масштабирования. Астатизм системы только лишь относительно задающего воздействия может быть обеспечен значительно более простыми способами: неединичной обратной связью и масштабированием.
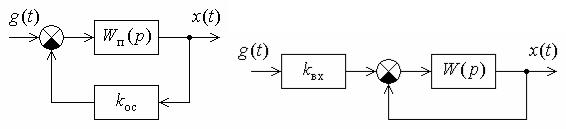
Структурная схема системы с неединичной обратной связью показана на рис. 11.9, а. В установившемся режиме регулируемая координата x(t) связана с постоянным задающим воздействием g0 соотношением
xуст kпg0 /(1 kпkос), |
(11.22) |
где kп – передаточный коэффициент прямой цепи системы; kос – передаточный коэффициент обратной связи.
а |
б |
Рис. 11.9
257
Если выполнить основную обратную |
связь системы |
с передаточным коэффициентом kос 1 1/kп, то |
xуст g0, и система |
будет астатической относительно задающего воздействия. Структурная схема системы с масштабированием входной
величины показана на рис. 11.9, б. Ее особенность – наличие усилительного звена с передаточным коэффициентом kвх на входе. В установившемся режиме
xуст kвхkg0 |
/(1 k), |
(11.23) |
где k – передаточный коэффициент разомкнутого контура. |
|
|
При kвх 1 1/k получаем |
xуст g0 и система |
является |
астатической относительно задающего воздействия.
Недостаток этих способов в том, что астатизм обеспечивается только при сохранении указанных соотношений между передаточными коэффициентами. Неточное определение передаточного коэффициента какого-либо элемента системы и его изменение в процессе эксплуатации ведет к появлению статической ошибки. Астатизм, достигнутый с помощью интегрирующего или изодромного звена, сохраняется и при изменении параметров системы.
11.3. Инвариантные и комбинированные САУ
Одним из способов, позволяющих получить высокую точность в системах автоматического регулирования, является использование методов теории инвариантности. Система автоматического регулирования является инвариантной по отношению к возмущающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, регулируемая величина и ошибка системы не зависят от этого воздействия. Система автоматического регулирования является инвариантной по отношению к задающему воздействию, если после завершения переходного процесса, определяемого начальными условиями, ошибка системы не зависит от этого воздействия.
Теория инвариантности систем управления развивалась в трудах Г. В. Щипанова, Б. Н. Петрова и др.
Основной способ построения инвариантных систем состоит в применении комбинированного управления.
258
