
Если внешнее воздействие допускает прямое или косвенное измерение, то точность системы может быть повышена за счет комбинированного управления. Под комбинированным управлением понимается такой метод построения автоматических систем, когда наряду с замкнутым контуром регулирования по отклонению используется регулирование по задающему или возмущающему воздействию. Таким образом, комбинированное управление сочетает принципы регулирования по замкнутому и разомкнутому циклам. При построении систем комбинированного управления создается второй канал прохождения задающего или возмущающего воздействия и обеспечиваются условия компенсации этих воздействий на ошибку системы.
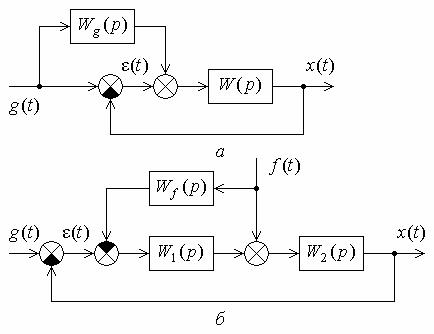
Рассмотрим случай комбинированного управления по задающему воздействию. Структурная схема системы управления изображена на рис. 11.10, а.
Рис. 11.10
Если осуществлять регулирование только по отклонению, т. е. положить Wg (p) 0, то
x(p) |
W(p) |
g(p), |
(11.24) |
|
1 W(p)
где W(p) – передаточная функция разомкнутой системы.
259

При введении регулирования по задающему воздействию получим
x(p) |
W(p)[1 Wg (p)] |
(11.25) |
g(p). |
1 W(p)
Из (11.25) видно, что введение регулирования по задающему воздействию не меняет характеристического уравнения системы, работающей по отклонению, так как знаменатели в (11.24) и (11.25) одинаковы. Это означает, что при комбинированном управлении сохраняются не только условия устойчивости, но и оценки качества переходного процесса, основанные на использовании корней характеристического уравнения.
Передаточная функция по ошибке
|
1 Wg (p)W(p) |
|
|||||
Фεg |
(p) |
|
|
|
|
. |
(11.26) |
|
|
|
|
||||
Положив |
|
1 W(p) |
|
||||
|
|
|
1 |
|
|
|
|
|
Wg (p) |
|
, |
|
(11.27) |
||
|
|
|
|
||||
|
|
W(p) |
|
||||
получим Фεg (p) 0, т. |
е. ошибка |
системы не будет |
зависеть от |
||||
задающего воздействия. |
|
|
|
|
|
|
|
Условие (11.27) называется условием полной инвариантности (т. е. независимости) системы по отношению к задающему воздействию. Поскольку реальные системы представляют собой различные комбинации инерционных и интегрирующих звеньев, у которых порядок полинома числителя меньше порядка полинома
знаменателя, то реализацию |
|
условия |
(11.27) можно |
представить |
||||
в виде |
|
|
|
|
|
p2 |
|
|
W |
g |
(p) a |
0 |
a p a |
2 |
. |
(11.28) |
|
|
|
1 |
|
|
|
|||
Для астатических систем a0 0. Из (11.28) видно, что при комбинированном управлении для получения полной инвариантности необходимо вводить первую и высшие производные от задающего воздействия. На практике получение высших производных (выше второй) затруднительно, поэтому может быть получена не полная, а частичная инвариантность с точностью до некоторой величины . Однако и частичная инвариантность является весьма благоприятной в смысле повышения точности САУ. Так, например, введением одной первой производной от входного воздействия в системе с астатизмом
260
первого порядка можно добиться равенства нулю скоростной ошибки, т. е. повысить порядок астатизма на единицу.
Комбинированное управление может быть использовано также для уменьшения влияния контролируемого возмущающего воздействия f (t), приложенного в какой-либо точке системы (рис. 11.10, б). При этом передаточная функция по возмущению
Фεf |
(p) |
W2(p) Wf (p)W(p) |
, |
(11.29) |
|
||||
где W(p) W1(p)W2(p) |
|
1 W(p) |
|
|
– передаточная функция |
разомкнутой |
|||
системы; Wf (p) – передаточная функция по данному возмущению
в разомкнутой системе.
Полная инвариантность может быть получена при Фεf (p) 0,
т. е. |
|
|
|
||
Wf (p) |
W2(p) |
|
1 |
. |
(11.30) |
|
|
||||
|
W(p) |
W1(p) |
|
||
В практическом плане можно говорить, |
таким образом, не |
||||
о полной инвариантности от внешних воздействий, а о возможности существенного повышения качества переходных процессов путем применения форсирующих воздействий по производным от этих возмущений – об инвариантности с точностью до малой величины ε.
Пример 11.4. Определить требуемый уровень компенсирующего сигнала по первой производной от входного воздействии, при котором устраняется скоростная ошибка системы
(рис. 11.10, а), где
|
W(p) |
|
k |
; Wg (p) kg p. |
|
|||||||
|
p(Tp 1) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Уравнение ошибки относительно входного |
||||||||||||
воздействия |
W(p) |
Wg (p)W(p) |
1 Wg (p)W(p) |
|
||||||||
|
|
|||||||||||
(t) g(t) |
|
|
g(t) |
|
|
|
|
g(t) |
|
|
g(t). |
|
|
1 W(p) |
1 W(p) |
||||||||||
|
1 W(p) |
|
|
|||||||||
Передаточная функция замкнутой системы по ошибке |
|
|||||||||||
|
|
1 Wg |
(p)W(p) Tp2 p kgkp |
|
||||||||
|
Фε(p) |
|
|
|
|
|
|
. |
|
|||
|
1 W(p) |
|
|
|
|
|||||||
|
|
|
|
|
|
Tp2 p k |
|
|||||
261

Коэффициент скоростной ошибки
C2 Фεp(p) p 0 1 kkgk .
Условие устранения скоростной ошибки 1 kgk 0.
Следовательно, kg 1/k.
Контрольные вопросы
1.Назовите основные способы включения корректирующих устройств в САУ.
2.Перечислите основные последовательные корректирующие звенья САУ.
3.Какие основные алгоритмы управления вы знаете?
4.Перечислите основные виды обратных связей.
5.Что такое изодомная обратная связь, особенности ее действия?
6.Как влияет повышение коэффициента передачи разомкнутой системы на статическую точность?
7.Как можно повысить порядок астатизма системы управления?
8.Как с помощью неединичной обратной связи можно из статической сделать систему астатической?
9.В чем заключается метод компенсации возмущений?
10.Что такое инвариантность системы и каковы условия ее получения?
11.Что такое инвариантность системы с точностью до малой величины ε?
12.В чем заключаются особенности построения комбинированных систем?
262
