

величина по своим свойствам становится близкой к непрерывной величине.
Сетка уровней квантования и диапазон изменений входной величины всегда связаны между собой: число уровней квантования будет
N = |
x |
max |
− x |
min |
. |
||
|
|
|
|||||
|
|
|
q |
|
|||
|
|
|
|
|
|
||
Из статической характеристики квантователя следует, что число |
|||||||
уровней квантования |
|
|
|
|
|
|
|
N = 2 |
m |
−1, |
|
||||
|
|
|
|||||
где m – число двоичных разрядов аналого-цифрового преобразователя.
Тогда для представления всех кодовых комбинаций необходимо иметь код, состоящий из m двоичных разрядов, где
m log2 Nmax .
Если дискретный (квантованный) сигнал определять числом целых уровней, укладывающихся в текущем значении непрерывной
величины |
X |
, то ошибка квантования будет положительной и лежать |
|
|
в пределах 0 – q . Ее можно уменьшить вдвое, если дискретные
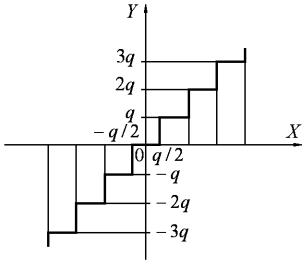
значения определять ближайшим уровнем квантования, т. е. округлять их до следующего уровня, если входная величина переходит за середину очередного шага квантования. В этом случае
ошибка квантования будет лежать в пределах |
q / 2 |
. Для |
осуществления такого квантования выполняющее его устройство должно иметь статическую характеристику, показанную на рис. 11.12. (Очевидно, что устройство, осуществляющее квантование по числу пройденных уровней, будет выполнять квантование до ближайшего уровня, если ко входному сигналу X добавить смещающий сигнал q / 2 , равный половине шага квантования). Во
всех цифровых САУ преобразование непрерывной величины в цифровую осуществляется путем квантования с округлением до ближайшего уровня.
Преобразователь Ц-Н цифровой величины в непрерывную
преобразует выходной сигнал ЦВМ в ступенчатую функцию |
Y (nT |
п |
) |
, |
|
|
|
которая изменяется скачком в моменты
nTп
, а в промежутке между
этими моментами сохраняется неизменной или изменяется по определенному экстраполяционному закону (линейно, квадратично и
308
т. п.). Таким образом, в первом случае сигнал квантованному по уровню сигналу с АИМ при γ =1
Y (nTп ) подобен
(см. рис. 11.11.).
Рис. 11.12. Статическая характеристика квантователя преобразователя Н-Ц
Основные достоинства цифровых САУ определяются теми возможностями, которые возникают в результате применения цифровой техники. Это прежде всего высокая точность, помехозащищенность и возможность реализации очень сложных алгоритмов управления, какие только доступны современным ЦВМ. Кроме того, к цифровым САУ в полной мере относится и такое достоинство импульсных систем, как возможность осуществления многоточечного управления. Высокая точность цифровых систем объясняется цифровой формой представления в ней перерабатываемой управляющим устройством информации. Точность всех операций при этом практически не имеет предела и определяется числом разрядов цифрового кода, которым представлены сигналы.
Помехозащищенность цифровых систем выше, чем у импульсных, благодаря кодовому представлению информации. Она может быть увеличена практически неограниченно за счет введения избыточности, позволяющей автоматически обнаруживать и исправлять возможные ошибки и искажения, возникающие при передаче и переработке цифровой информации.
Разумеется, все эти достоинства цифровых систем достигаются ценой значительно большей их сложности и стоимости по сравнению с другими системами. Поэтому цифровые САУ применяются только в тех случаях, когда иными, более простыми средствами задача решена
309
быть не может. Так, цифровыми, делаются даже простые по алгоритму работы системы управления и регулирования, если от них требуется большая точность. Например, существуют цифровые системы программного регулирования с цифровым задатчиком программы, цифровые следящие системы с цифровыми измерителями рассогласования и шаговыми исполнительными двигателями или другими исполнительными органами дискретного действия. Широко применяются цифровые регуляторы, особенно интегрального типа, в которых цифровое представление регулируемой величины позволяет осуществить интегрирование с любой степенью точности.
Однако основная область применения цифровых систем – это когда нужны системы с достаточно сложным алгоритмом преобразования информации в управляющем устройстве, требующим применения ЦВМ. В этом случае в состав управляющего устройства могут входить ЦВМ вплоть до больших машин универсального типа и даже комплекса таких машин. Примерами таких цифровых САУ являются системы управления судами, самолетами и ракетами с помощью малогабаритных бортовых ЦВМ, системы централизованного автоматического управления производством. В таких системах количество входных и выходных величин объекта управления может измеряться сотнями, а расстояния, на которые передаются эти величины, – многими километрами, а в отдельных случаях и тысячами километров.
Область применения цифровых систем в настоящее время быстро расширяется по мере совершенствования ЦВМ.
11.5.2. Особенности динамики цифровых систем автоматического управления. Наличие в цифровой системе квантования по уровню делает ее принципиально нелинейной, как и систему релейного действия. При этом, как и в релейных САУ, в цифровых системах возможна неустойчивость в малом с установлением автоколебаний, амплитуда которых определяется зоной нечувствительности системы, равной шагу квантования. Правда, поскольку шаг квантования в цифровых САУ обычно мал, возможная амплитуда таких автоколебаний тоже достаточно мала.
Статическая точность цифровой САУ определяется шагом квантования, минимальная величина которого ограничена точностью
310
измерения выходных величин объекта, а также возможной точностью преобразования их в цифровую форму. При уменьшении шага квантования q , т. е. при увеличении числа уровней квантования и
числа разрядов цифрового кода, цифровая система приближается по своим свойствам к импульсной системе. При достаточной малости шага квантования q квантованием по уровню можно пренебречь и
приближенно рассматривать цифровую систему как импульсную систему. Такая импульсная система (получаемая из цифровой при q → 0 ) называется предельной импульсной системой.
Особенностью динамики цифровых САУ по сравнению с импульсными является обязательное наличие фиксированного временного запаздывания в управляющем устройстве, определяемого длительностью одного цикла переработки информации в ЦВМ.
11.6. Методы исследования цифровых систем автоматического управления
Математическое описание цифровых САУ осуществляется, как и импульсных САУ, с помощью разностных уравнений и дискретного преобразования Лапласа путем предварительной замены действующих в непрерывной части системы непрерывных величин фиктивными дискретными в виде решетчатых функций. Однако в связи с тем, что в отличие от импульсных систем в цифровых САУ имеется квантование по уровню, структурная схема цифровой САУ содержит, помимо импульсных элементов, нелинейные звенья – квантователи, описываемые многоступенчатой релейной статической характеристикой.
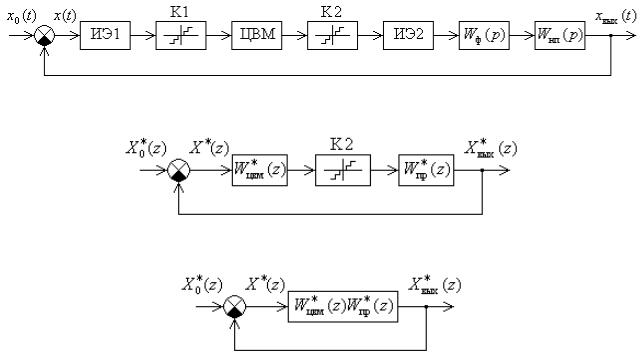
На рис. 11.13, а показана структурная схема цифровой САУ, соответствующая схеме на рис. 11.11. Здесь преобразователь Н-Ц предоставлен последовательным соединением импульсного элемента ИЭ1 и квантователя К1. Импульсный элемент ИЭ1 осуществляет квантование по времени, преобразуя входную непрерывную функцию x(t) в последовательность ее дискретных значений через период
квантования Tп , т. е. в решетчатую функцию x[nTп ]. Далее
квантователь К1 статическая характеристика которого показана на рис. 11.12, осуществляет квантование по уровню этих дискретных значений, преобразуя каждое значение x[n] в дискретную величину в
311
виде ближайшего целого числа уровней (шагов) |
q . Это число |
вводится в ЦВМ в определенной (обычно двоичной) системе счисления.
ЦВМ производит вычисления над этой последовательностью чисел в соответствии с заложенной в нее программой (алгоритмом) и выдает через период Tп очередной результат yцвм [nTп ] тоже в виде
числа. Выходная величина ЦВМ может быть выражена через входную с помощью разностного уравнения. Если выполняемые ЦВМ операции являются линейными, соответствующее разностное уравнение будет линейным. В этом случае ЦВМ может быть описана дискретной передаточной функцией. Это имеет место, например, когда алгоритм работы заключается в вычислении линейной функции отклонения выходной величины объекта от ее заданного значения, интегралов и производных, служащих для коррекции.
а
б
в
Рис. 11.13. Структурные схемы цифровой САУ
Преобразователь Ц-Н представлен в виде квантователя по
уровню К2, идеального |
-импульсного |
элемента |
ИЭ2 и |
формирующего элемента ФЭ |
с передаточной |
функцией |
W ф( p) . |
Формирующий элемент преобразователя Ц-Н представляет собой
312
экстраполятор, сохраняющий сигнал на выходе ЦВМ в течение такта работы машины, т. е. периода Tп , за который она вырабатывает
следующее дискретное значение выходного сигнала. Простейший такой экстраполятор, называемый экстраполятором нулевого порядка, удерживает выходной сигнал на исходном уровне, т. е. выдает прямоугольные импульсы шириной Tп . Соответственно передаточная функция формирующего элемента при этом
определяется формулой (11.3) при |
Tи = Tп . Существуют |
экстраполяторы, изменяющие в течение периода Tп |
выходной сигнал |
по линейному закону (экстраполяторы первого порядка), по квадратичной параболе (экстраполяторы второго порядка) и т. д.
Число уровней (ступеней статической характеристики) квантователей К1 и К2 в общем случае различно. У входного квантователя К1 число уровней обычно бывает большим, поскольку оно определяется числом разрядов ЦВМ, которое, в свою очередь, определяет точность обработки входной информации. В наиболее распространенном случае преобразования непрерывной величины в
двоичный код число уровней у квантователя К1 равно |
2 |
m |
− 1 |
, где m – |
|
||||
|
|
|
число двоичных разрядов входного преобразователя. Соответственно
при обычном для входного преобразователя значении |
m =10 20 |
|||||
число уровней будет равно |
10 |
3 |
10 |
6 |
. Поэтому |
чаще всего |
|
|
|||||
квантованием сигнала на входе ЦВМ можно пренебречь, заменив статическую характеристику квантователя К1 линеаризующей ее прямой линией.
Число уровней выходного квантователя К2 определяется требованиями статики и динамики САУ и обычно бывает небольшим вплоть до единицы, что соответствует обычному релейному управлению объектом. Последний случай относится, например, к оптимальному по быстродействию управлению.
На рис. 11.13, б показана структурная схема цифровой САУ, преобразованная в соответствии с порядком, изложенным в разделе 11.3. Схема относится к случаю, когда непрерывная часть системы и алгоритм работы. ЦВМ линейные. Квантование на входе ЦВМ не учитывается. Переменные заменены решетчатыми функциями.
Выходная величина системы
X вых
(z)
показана в общем случае в
313
промежуточной точке непрерывной |
части |
|
|
воздействие Fпр (z) приведено ко входу ЦВМ. |
|
Дискретная передаточная функция |
|
Wцвм (z) |
|
системы, внешнее
описывает ЦВМ со
входным
функция
импульсным элементом ИЭ1. Дискретная передаточная
|
описывает участок системы от входа импульсного |
Wпр (z) |
элемента
величины
ИЭ2
X вых
соответственно |
до места нахождения выходной |
(z) непрерывной |
части системы. |
Если вследствие достаточной малости шага квантования выходного квантователя К2 им можно пренебречь, получим предельную импульсную систему, схема которой показана на рис. 11.13, в. Однако между этими схемами имеется существенная разница в отношении выражений для описывающих их дискретных передаточных функций. Предельная импульсная схема цифровой САУ содержит два импульсных элемента, т. е. состоит из двух последовательно включенных разомкнутых импульсных участков со своими импульсными элементами. Соответственно каждый такой участок описывается своей дискретной передаточной функцией
Wцвм (z) и
W пр
(z)
,
а дискретная передаточная функция всей
разомкнутой системы будет равна произведению этих дискретных передаточных функций, т.е. W (z) = Wцвм (z)Wпр (z) . Только в этом случае можно перемножать дискретные передаточные функции.
Для схемы, состоящей из одного импульсного элемента и последовательно включенных за ним непрерывных звеньев нельзя находить дискретную передаточную функцию всей цепочки путем вычисления дискретных передаточных функций по непрерывным передаточным функциям отдельных звеньев и последующего их
перемножения. Передаточную функцию W.пп (z) надо находить
только по передаточной функции всей непрерывной части
W |
|
( |
|
||
пр |
|
|
p)
.
Методика исследования цифровых САУ в случае, когда можно пренебречь квантованием по уровню, сводится к исследованию предельной импульсной системы.
При достаточно большом шаге квантования сведение цифровой САУ к предельной импульсной с заменой квантователя источником шума, некоррелированного с квантуемым сигналом, может привести
314
к недопустимо большой ошибке. В этом случае цифровая система должна исследоваться как существенно нелинейная с учетом наличия в ней квантователя подобно релейной САУ без вибрационной линеаризации.
Коррекция цифровых САУ осуществляется прежде всего путем выбора соответствующего алгоритма ЦВМ, входящей в состав управляющего устройства. При этом, как уже отмечалось, усложнение алгоритма работы управляющего устройства в данном случае не ведет к снижению точности его реализации, как у систем непрерывного действия.
Контрольные вопросы
1.Виды квантования сигналов?
2.Какие существуют виды импульсной модуляции?
3.Основные достоинства импульсных САУ?
4.Различия математического описания идеального импульсного элемента и реального импульсного элемента?
5.Передаточная функция формирующего элемента?
6.Что дает переход к решетчатым функциям?
7.Что такое дискретное преобразование Лапласа?
8.Что такое Z -преобразованиие?
9.Особенность частотных характеристик импульсных систем?
10.С помощью каких методов выполняется исследование устойчивости линейных импульсных САУ?
11.Как осуществляется коррекция импульсных систем?
12.Различие сигналов в цифровых и импульсных системах автоматического управления?
13.Что входит в состав цифровой системы автоматического управления?
14.Помехозащищенность каких систем выше: цифровых или импульсных?
15.Область применения цифровых систем.
16.Чем определяется статическая точность цифровой САУ?
17.Какую характеристику имеет квантователь сигналов?
18.Виды коррекции цифровых САУ?
20. Назовите положительные свойства цифровых систем автоматического управления.
315
