
функции z = e |
q |
, |
которая после подстановки |
q = |
jω |
принимает вид |
||||
|
||||||||||
e |
jω |
, т. е. становится периодической функцией |
ω |
. |
|
|
||||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
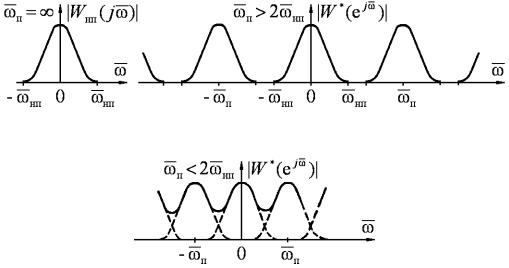
Физически |
периодичность |
частотной |
|
характеристики |
||||
импульсной, системы объясняется следующим образом. Выходной сигнал импульсного элемента и соответственно воздействие на непрерывную часть системы определяются значением входного сигнала только в дискретные моменты времени через промежуток Tп . Поэтому при гармоническом воздействии на импульсный элемент выходной сигнал системы не изменится при изменении частоты гармонического сигнала ω на любую величину, кратную ωп , т. е.
выходной сигнал будет
ω + kωп , где |
k = 0, 1, |
k = 0, 1, 2, , |
выходной |
одним и тем же при всех частотах, равных
2, . В частности, при |
ω = kωп , где |
сигнал будет равен реакции на постоянное
входное воздействие. В результате при снятии частотной характеристики путем неограниченного увеличения частоты сигнала на входе импульсного элемента должна получиться периодическая характеристика, показанная на рис. 11.9, б или в.
а |
б |
в
Рис. 11.9. Амплитудная частотная характеристика разомкнутой непрерывной (а) и импульсной (б и в) систем
Явление периодичности частотной характеристики импульсных систем можно трактовать и с точки зрения процесса импульсной модуляции, происходящего в импульсном элементе. При модуляции входным непрерывным сигналом последовательности импульсов
298
образуются боковые спектры частот. Число этих спектров бесконечно, поскольку бесконечно узкий импульс содержит бесконечное число гармоник.
Периодичность частотных характеристик импульсных систем, а также их симметричность относительно нулевой частоты, т. е, относительно оси ординат на рис. 11.9 означает, что для их полного описания достаточно иметь частотные характеристики в диапазоне относительных частот ω от 0 до + π , что соответствует абсолютным значениям частоты 0 0,5 ωп .
Ранее было сказано, что при достаточно большой частоте повторения импульсов импульсная САУ будет эквивалентна системе непрерывного действия. Из рассмотрения частотных характеристик импульсной системы (рис. 11.9, б и в) можно количественно определить условие такой эквивалентности. Оно сводится к двум следующим неравенствам:
где
ω f
ω |
п |
2ω |
нп |
; |
|
|
(11.13) |
|
|
|
|
|
|
|
|||
ω |
|
ω |
|
− ω |
|
, |
||
f |
п |
нп |
|
|||||
|
|
|
|
|
|
|||
спектр (наибольшая частота) внешнего воздействия,
приведенного ко входу импульсного элемента.
При выполнении первого неравенства частотные характеристики непрерывной и импульсной систем в пределах полосы пропускания непрерывной части совпадают. Поскольку боковые частоты, существующие на выходе импульсного элемента, не пройдут на выход непрерывной части системы, играющей роль фильтра нижних частот, импульсная система будет реагировать на низкочастотные внешние воздействия подобно непрерывной системе.
Характеристика на рис. 11.9, б соответствует выполнению первого условия, а характеристика на рис. 11.9, в не удовлетворяет ему. В результате частотная характеристика импульсной системы в пределах полосы пропускания непрерывной части системы оказывается искаженной (из-за влияния боковых частот) и отличается от частотной характеристики непрерывной части. Поэтому при невыполнении этого условия импульсная САУ будет отличаться по своим свойствам от САУ непрерывного действия с той же непрерывной частью, и при ее исследовании необходимо учитывать импульсный характер работы системы (в частности, описывать ее дискретной передаточной функцией).
299
Второе неравенство (11.13) ограничивает частоту
ω f
приведенного внешнего воздействия таким образом, чтобы частотный спектр этого воздействия, равный после прохождения
через импульсный элемент |
kωп ω f , где |
k = 0, 1, 2, , был в |
пределах полосы пропускания нп |
непрерывной части системы таким |
же, как и при отсутствии импульсного элемента, т. е. не давал боковых частот. При невыполнении второго условия на выходе импульсной системы появятся низкочастотные составляющие процесса, которые отсутствуют в непрерывной системе и возникают при прохождении внешнего воздействия через импульсный элемент.
При выполнении условий (11.13) наличием квантования по времени в системе можно пренебречь и рассматривать систему как САУ непрерывного действия. Условия (11.13) представляют собой известную теорему Котельникова – Шеннона (теорему отсчетов) об условии неискаженной передачи непрерывного сигнала конечным числом ero дискретных значений применительно к САУ с АИМ.
Частотные характеристики импульсной системы можно получить не только по дискретной передаточной функции, но и чисто графическим построением по частотной характеристике непрерывной части системы. Методика построения основана на рассмотренной выше связи дискретной передаточной функции с непрерывной передаточной функцией.
11.4. Методы исследования импульсных систем автоматического управления
При выполнении условия (11.13) импульсная система сводится к непрерывной и соответственно может исследоваться как САУ непрерывного действия известными методами.
Если это условие не выполняется, импульсная САУ должна исследоваться с учетом квантования по времени, т. е. на основе ее описания с помощью дискретной передаточной функции или соответствующих частотных характеристик, рассмотренных в предыдущем параграфе. Это придает определенную специфику исследованию, хотя сами методы исследования точности, устойчивости и качества переходных процессов остаются прежними.
300
11.4.1. Исследование устойчивости. Исследование устойчивости линейных импульсных САУ осуществляется с помощью известных критериев устойчивости линейных систем – критериев Рауса – Гурвица, Найквиста, Михайлова, модифицированных с учетом особенностей описания импульсных систем.
Как и у непрерывных систем, в импульсной системе переходная составляющая процесса управления определяется знаменателем
передаточной функции
|
(z) |
Ф |
(12.8) замкнутой системы
1 + W
(z)
,
т.е. 1 +W (eq ) . Соответственно, как и у САУ непрерывного действия,
общим условием устойчивости импульсной системы является нахождение всех полюсов передаточной функции замкнутой
системы, т. е. нулей 1 + W |
|
(e |
q |
) |
|
|
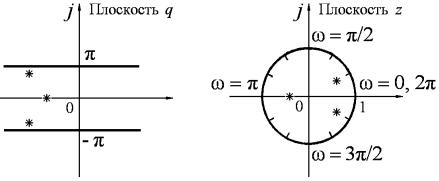
переменной q (рис. 11.10, а). Дискретная передаточная
в левой полуплоскости комплексной
функция |
Ф |
|
(e |
q |
) |
является функцией |
|
|
e |
q |
, которая представляет собой периодическую функцию мнимой |
|
части q с периодом 2π , т.е.
e |
q |
= e |
α jω |
|
|
=
e |
α |
|
j(2kπ+ω)
.
Следовательно, передаточная функция
|
q |
) |
Ф |
(e |
является тоже
периодической функцией вдоль мнимой оси, и поэтому при изучении полюсов этой передаточной функции на комплексной плоскости q
достаточно рассмотреть их в полосе
(рис. 11.10. а).
π
вдоль действительной оси
а |
б |
Рис. 11.10. Расположение полюсов передаточной функции устойчивой импульсной системы в комплексных плоскостях q и z
301

|
Если перейти от q к |
z = e |
q |
, то нахождению нулей |
z многочлена |
||||
|
|
||||||||
1 + W |
|
(z) |
левее мнимой оси плоскости |
q |
соответствует на плоскости |
||||
|
|||||||||
z
нахождение нулей
z
многочлена
1 + W |
|
(z) |
|
внутри окружности
единичного радиуса с центром в начале координат (рис. 11.10. б). Иными словами, эта окружность является границей устойчивости
системы на плоскости z . Действительно, при |
q = |
jω |
(мнимая ось на |
плоскости q) модуль | z |=| e jω |= 1. |
|
|
|
Чтобы применить критерий устойчивости Рауса – Гурвица к импульсной системе, произведем замену переменной, введя новую переменную w подстановкой
|
z = |
w +1 |
. |
(11.14) |
|
w −1 |
|||
|
|
|
|
|
Области устойчивости в виде круга радиусом 1 на плоскости z |
||||
(или в виде полосы шириной |
π |
левее мнимой оси на плоскости q ) |
||
|
||||
соответствует вся левая полуплоскость комплексной плоскости новой переменной w . Границей устойчивости при этом является вся мнимая
ось: изменению |
ω |
на |
2π |
соответствует изменение |
w |
от |
− j |
до |
|
|
|
|
|
|
|
|
+
j
. Таким образом, в
результате такой подстановки получается
уравнение, условия устойчивости для которого совпадают с условиями устойчивости непрерывных систем. Поэтому к нему непосредственно могут быть применены все известные для непрерывных систем критерии устойчивости.
Для применения критерия Рауса – Гурвица надо использовать
знаменатель |
D |
|
(z) |
|
Пример 11.3.
передаточной функции системы.
У системы первого порядка
D |
|
(z) = a |
0 |
1. |
|
||||
|
|
z + a |
Решение. После подстановки сюда выражения (12.20) получаем:
D (z) = a |
|
w +1 |
+ a = |
(a0 + a1)w + a0 − a1 |
. |
|
|
|
|
|
|||
0 w −1 |
|
|||||
|
1 |
w −1 |
||||
Соответствующее характеристическое уравнение будет
(a0
+ a )w + a |
0 |
1 |
− a1
=
0
,
и, следовательно, условия устойчивости Рауса – Гурвица, заключающиеся, как известно, в данном случае в положительности
302

коэффициентов характеристического неравенствам:
a |
0 |
+ a |
0; |
||
|
1 |
|
|
||
a |
|
− a |
0. |
||
0 |
|
||||
|
1 |
|
|||
уравнения, сведутся к
. |
(11.15) |
Пример 11.4. Для системы второго порядка
|
|
D |
|
(z) = a |
|
z |
2 |
+ a z |
||
|
|
|
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
1 |
|
Решение. Соответственно |
|
|
|
|
|
|||||
|
|
|
|
|
w +1 |
|
2 |
|||
D |
|
(z) = a |
1 |
|||||||
|
0 |
|
|
|
|
|||||
|
w −1 |
|
+ a |
|||||||
|
|
|
|
|
|
|||||
и характеристическое уравнение будет
+
w w
a2 .
+1 + a2
−1
(a |
|
+ a |
+ a |
|
)w |
2 |
+ 2(a |
|
− a |
|
)w + (a |
|
0 |
2 |
|
0 |
2 |
0 |
|||||||
|
1 |
|
|
|
|
|
|
Отсюда получаются условия устойчивости:
a0 + a1 + a2 |
0; |
||||
a0 |
− a2 0; |
|
|||
|
|||||
a |
0 |
− a |
+ a |
2 |
0. |
|
1 |
|
|
||
−a1+a2 ) = 0 .
(11.16)
Аналогично можно получить условия устойчивости для систем более высоких порядков, однако они оказываются значительно более сложными, чем для систем непрерывного действия.
11.4.2. Исследование точности и качества. Исследование точности и качества переходных процессов импульсных систем осуществляется с помощью тех же методов и критериев, что и для непрерывных САУ. Соответственно методы синтеза импульсных систем тоже заимствованы из теории САУ непрерывного действия. В частности, и здесь широко применяется синтез на базе логарифмических частотных характеристик. При этом для возможности применения методики синтеза непрерывных САУ удобно использовать подстановку (11.14).
Построение переходных процессов в импульсных САУ осуществляется путем решения уравнения (11.7)
X |
|
(z) = Ф |
|
(z) X |
|
(z) |
вых |
|
0 |
||||
|
|
|
|
|
описанным выше образом с использованием таблиц дискретного преобразования Лапласа или графически с помощью методов, и в том
303
числе по частотной характеристике системы (метод трапецеидальных характеристик).
Здесь есть только одна особенность по сравнению с САУ непрерывного действия – в результате построения находится не
действительная непрерывная |
выходная |
величина |
xвых (t) , а |
решетчатая функция xвых [n], |
т.е. значения |
выходной |
величины в |
дискретные моменты времени через период Т п . Это цена упрощения
математического описания импульсной системы путем перехода от непрерывных функций времени к решетчатым функциям.
В тех случаях, когда требуется знание значений выходной величины в промежуточные моменты времени, т. е. внутри интервала
Т п |
может быть применено модифицированной дискретное |
преобразование Лапласа. Оно оперирует
сдвинутыми относительно моментов |
t |
|
|
промежуток времени εT п , где значение |
ε |
решетчатыми функциями,
= T n |
на фиксированный |
п |
берется в диапазоне 0 – 1.
Такая решетчатая функция обозначается
x[n,
ε]
.
Пользуясь модифицированным дискретным преобразованием Лапласа, можно найти соответствующую дискретную передаточную
функцию системы
|
(z, ε) |
Ф |
и по ней – кривую переходного процесса
x(n,
ε)
, определяющую
значения выходной величины в моменты
времени
t
=
(n +
ε)Tп
, т. е. в точках внутри интервалов квантования по
времени.
|
Для модифицированного дискретного преобразования Лапласа |
существуют формулы и таблицы, аналогичные формулам и таблицам |
|
для |
простого преобразования Лапласа. Строя переходный процесс |
для |
нескольких значений ε , принципиально можно получить любое |
число точек реального непрерывного процесса |
x |
вых |
(t) |
. |
|
|
|
Коррекция импульсных систем может осуществляться с помощью обычных корректирующих звеньев непрерывного действия, вводимых в непрерывную часть системы, и с помощью корректирующих звеньев импульсного действия. Последние включаются после импульсного элемента. Как и корректирующие звенья непрерывного действия, они могут быть последовательными и параллельными. Например, вместо пропорциональнодифференцирующего корректирующего звена непрерывного действия в импульсной САУ может быть применено импульсное
304
звено с соответствующей дискретной передаточной функцией. Получение сигнала по производной будет осуществляться при этом в виде сигнала по первой разности дискретных значений входного сигнала. Соответствующее корректирующее звено должно запоминать очередное дискретное значение входного сигнала x[n] и с
поступлением следующего его значения
x[n +1]
выдавать на выходе
дискретный
значение |
x[n |
+
сигнал разности
1].
x[n] =
x[n +1] −
x[n]
,
запоминая
11.5. Определение и особенности динамики цифровых систем автоматического управления
11.5.1. Цифровые системы автоматического управления.
Цифровыми системами были названы дискретные системы, в которых происходит квантование как по уровню, так и по времени. Более точно цифровые системы – это системы, в которых существуют дискретные сигналы в виде цифрового кода. Цифровые САУ – это наиболее совершенные по своим алгоритмическим возможностям дискретные САУ.
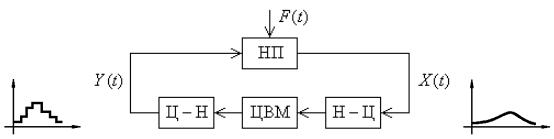
Рис. 11.11. Цифровая система автоматического управления
В них в состав управляющего устройства входит цифровая вычислительная машина. Большинство цифровых САУ можно представить в виде схемы, показанной на рис. 11.11. Здесь НП – непрерывная часть системы (обычно это объект управления), ЦВМ – цифровая вычислительная машина; Н-Ц и Ц-Н – соответственно преобразователи непрерывной величины в цифровую и наоборот. Эти преобразователи связывают ЦВМ, у которой входная и выходная величины представлены в цифровой форме, с непрерывной частью системы.
305
Преобразование непрерывной величины в цифровую заключается в квантовании ее по времени, по уровню и представлении полученных дискретных значений в виде чисел, т. е. в цифровом коде. В зависимости от принципа действия преобразователя это преобразование может осуществляться либо путем последовательного выполнения перечисленных выше этапов, либо сразу в виде одной операции. Такое преобразование называется кодо-импульсной модуляцией. Поэтому цифровые системы иногда называют кодо-импульсными системами. Соответственно преобразование Н-Ц называют кодированием, а обратное преобразование Ц-Н – декодированием. В отличие от импульсной модуляции, применяемой в импульсных САУ, здесь каждое значение преобразуемой входной величины представляется не одним импульсом, модулируемый параметр которого (высота, ширина, фаза) пропорционален значению входной величины, а серией импульсов. Каждое численное значение входной величины представляется определенной комбинацией дискретных значений модулируемого параметра этих импульсов.
Любое число |
A |
можно представить в следующем виде |
|
|
A = a |
|
h |
m−1 |
+ a |
h |
m−2 |
+ + a |
|
1 |
+ a h |
0 |
m |
|
|
2 |
h |
|
||||||
|
|
|
|
m−1 |
|
|
|
1 |
|
=
m |
i −1 |
|
i |
||
|
||
a h |
|
|
i =1 |
|
,
где h – основание системы счисления; |
i |
– номер разряда; m – номер |
||||
старшего разряда |
числа (количество |
разрядов); |
ai |
– разрядные |
||
коэффициенты (от |
0 до m −1). |
|
|
во всех системах счисления |
||
Для формальной записи числа |
A |
|
||||
|
|
|
|
|
|
|
обычно используют только разрядные коэффициенты, т. е. запись в виде кода
A ~ am am−1 a2 a1.
Существуют различные цифровые коды.
Простейший из них – единичный код. В этом случае каждое значение дискретной величины представляется числом импульсов, равным числовому значению величины. В случае десятичного кода дискретная величина выражается в виде десятичного числа и представляется серией импульсов, число которых равно числу разрядов этого числа. Каждый импульс несет информацию о цифре определенного разряда, Для этого модулируемый параметр импульса принимает одно из десяти дискретных значений. Наибольшее
306
распространение получил двоичный код, соответствующий системе счисления с основанием 2. Каждый разряд двоичного числа может иметь только одно из двух значений: 0 или 1. Соответственно модулируемому параметру каждого импульса, представляющего значение одного из разрядов, тоже придается одно из двух крайних значений.
В связи с этим в современной цифровой технике получила
широкое применение двоичная система счисления ( h = 2 |
, |
a = 0 |
или 1), в которой |
|
|
A = a |
|
2 |
m−1 |
+ a |
|
2 |
m−2 |
+ + a |
|
1 |
+ a 2 |
0 |
m |
|
m−1 |
|
2 |
2 |
|
||||||
|
|
|
|
|
|
|
|
1 |
|
=
m |
i −1 |
i |
|
a 2 |
|
i =1 |
|
.
Например
3 |
+1 2 |
2 |
1 |
+1 2 |
0 |
13 =1 2 |
|
+ 0 2 |
|
~
1101
.
Знак величины передается с помощью отдельного импульса тоже с двумя возможными значениями модулируемого параметра. (В предельно простом случае, когда учитывается только знак входной величины, получается релейная двухпозиционная система с квантованием еще и по времени.)
Преобразование непрерывной величины в цифровой код принципиально содержит погрешность из-за квантования по уровню, т. е. округления численного значения преобразуемой величины до целого числа, соответствующего числу уровней квантования. Абсолютное значение погрешности квантования определяется величиной шага квантования. Шаг квантования q – это приращение
входной непрерывной величины |
X |
, соответствующее интервалу |
|
|
между двумя соседними уровнями квантования.
При квантовании по уровню текущее значение амплитуды аналоговой величины заменяется ближайшим дискретным значением амплитуды, выбранным на шкале разрешенных уровней. Таким образом, аналоговая величина при квантовании по уровню как бы накладывается на сетку горизонтальных линий, разнесенных на шаг квантования (квант) q .
При уменьшении величины шага квантования увеличивается число разрядов в выходном коде АЦП и уменьшается ошибка из-за квантования по уровню. При очень большом числе разрядов в выходном коде, т. е. при очень малой величине кванта, дискретная
307
