
вместе с остальной передаточной функцией формирующего элемента вносится в состав передаточной функции непрерывной части системы
Wпр ( p) = Wф ( p)Wнп ( p) .
Перенос внешнего воздействия на вход импульсного элемента осуществляется обычным пересчетом через передаточную функцию, как показано на рис. 11.5, в.
В результате двух указанных выше преобразований схема импульсной САУ с произвольной формой импульсов и внешним воздействием, приложенным в произвольной точке, приводится к типовой схеме, показанной на рис. 11.5, в. Это позволяет при исследовании различных реальных импульсных систем пользоваться единым математическим описанием и соответственно общей методикой.
Для общности на рис. 11.5, в в качестве выходной величины xвых , связь которой с внешним воздействием x0 нам требуется найти
в результате математического описания системы в виде передаточной функции или частотной характеристики, показана величина в произвольной точке непрерывной части системы.
Преобразование схемы САУ заключается в замене действующих в непрерывной части системы непрерывных сигналов на фиктивные дискретные сигналы. В результате получается система, в которой существуют только дискретные переменные. Это существенно упрощает математическое описание импульсной САУ путем применения вместо обычных дифференциальных уравнений разностных уравнений и соответственно вместо обычного преобразования Лапласа дискретного преобразования Лапласа.
а |
б |
в |
Рис. 11.7. Решетчатая функция
288

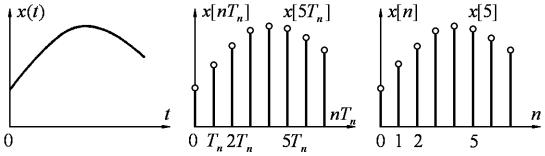
Возможность такой замены основана на том, что выходной сигнал импульсного элемента определяется значениями входного
сигнала |
x(t) |
в дискретные моменты времени в начале каждого |
периода
T п
повторения импульсов. Поэтому в работе импульсного
элемента ничего не изменится, если заменить непрерывную функцию x(t) на его входе дискретной функцией, значения которой в начале
каждого периода, т. е. в моменты
nT
п
, где
n = 1, 2, ,
совпадают со
значениями непрерывной функции, а в остальное время равны нулю. Такая дискретная функция называется решетчатой функцией и
обозначается |
x[nTп ] |
(рис. 11.7, б). Непрерывная функция x(t) |
является, очевидно, огибающей решетчатой функции
x[nTп
]
. При
рассмотрении дискретных функций удобно переходить к
относительному времени |
|
п , т. е. измерять время |
числом |
|
t |
= t / T |
|
периодов Tп . В этом случае относительный период повторения |
|||
импульсов Tп =1, а решетчатая функция обозначается в виде |
x[n], где |
||
n = 1, 2, , … (рис. 11.7, в). Это запись ее в нормированной форме. |
|||
Как известно, формула прямого преобразования Лапласа для непрерывных функций имеет следующий вид:
X ( p) = L{x(t)} = x(t)e− pt dt .
0
Для решетчатых функций времени может быть введено понятие дискретного преобразования Лапласа, определяемого формулами
|
|
|
|
|
|
− pnT |
|
X |
п |
|
|
п |
|
||
|
( p) = D{x[nT ]} = |
|
x[nT ]e |
|
п |
||
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
,
или в относительном времени:
|
|
|
−qn |
|
|
X |
(q) = D{x[n]} = x[n]e |
, |
|||
|
|
||||
|
|
n=0 |
|
|
где q = pTп – новая безразмерная комплексная переменная.
Для исследования импульсных систем большое распространение
получило так называемое |
Z |
-преобразование, которое связано |
|
с |
дискретным преобразованием Лапласа и вытекает из него. Под |
Z |
- |
||
|
|
|
|
|
преобразованием понимается изображение решетчатой функции. определяемой формулой
289

|
|
|
|
−n |
|
X |
(z) = Z{x[n]} = |
x[n]z |
|||
|
|
||||
|
|
|
n =0 |
|
,
где между комплексными переменными можно записать следующее соотношение:
z = e |
pT |
|
п |
||
|
=
e |
q |
|
.
Переход в структурной схеме, изображенной на рис. 11.5, в, от непрерывных функций времени к решетчатым функциям выполняется в следующем порядке.
Прежде всего, осуществляется переход от операторной записи к изображениям Лапласа непрерывных функций и затем к
относительному времени |
|
п . Переход к изображениям Лапласа |
|
t |
= t / T |
сводится к нахождению по оригиналу приведенного внешнего воздействия его изображения и к замене в передаточных функциях
оператора дифференцирования |
p на комплексную переменную p . |
||||||||
Переход далее к относительному времени заключается для |
|||||||||
изображения Лапласа внешнего воздействия в замене p на |
п , где |
||||||||
п |
|
– |
комплексная переменная в |
|
|
|
q / T |
||
|
относительном времени, и |
||||||||
q = T |
p |
|
|
п , т. е. в замене |
X 0 ( p) на |
|
|||
делении этого изображения на |
|
||||||||
|
|
|
|
T |
|
|
|
|
|
|
|
|
X 0 (q) = |
1 |
X 0 ( p) | p =q /T . |
|
|
||
|
|
|
|
|
|
||||
|
|
|
T |
|
|
п |
|
|
|
|
|
|
|
п |
|
|
|
|
|
Это |
|
непосредственно |
|
следует |
из |
|
формулы |
прямого |
|
преобразования Лапласа.
Соответственно переход к относительному времени для передаточных функций, поскольку они являются отношением изображений выходной и входной величин, сводится к замене p на
q / Tп
т. е. к замене
W ( p)
на
W ( p) | p =q /T п
.
Исключение составляет выражение для передаточной функции формирующего элемента в случае определения его через изображение функции времени по формуле (11.2). Осуществив в последнем изображении переход к относительному времени по вышеприведенному правилу, получаем:
W (q) = |
1 |
L[ y |
|
(t)] | |
|
, |
|
и |
p =q / T |
||||
ф |
Tп |
|
п |
|||
|
|
|
|
|||
|
|
|
|
|
|
|
т. е. искомое выражение
290
где
Wф (q) = |
1 |
Wф ( p) | p =q / T |
, |
|
T |
||||
|
|
п |
||
|
п |
|
||
|
|
|
||
Wф ( p) определяется по формуле (11.2). |
|
|||
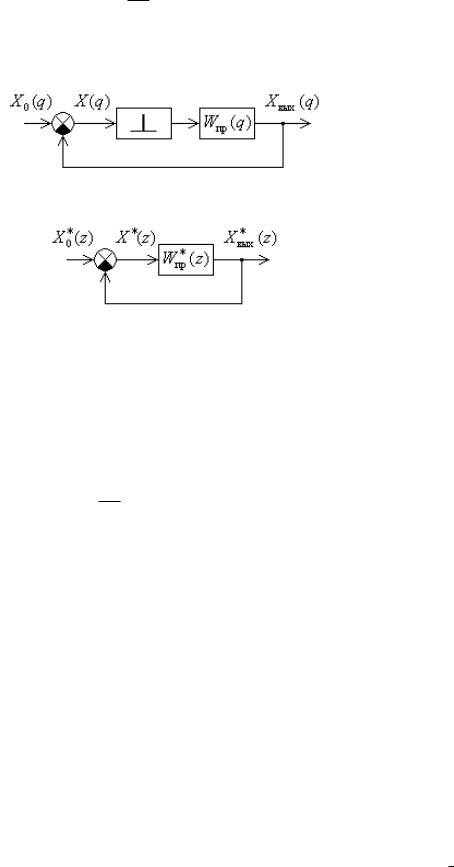
а
б
Рис. 11.8. Преобразование структурной схемы импульсной САУ
В результате перехода к изображениям Лапласа и относительному времени приведенная на рис. 11.5, в схема принимает вид, показанный на рис 11.8, а. Здесь
Wпр (q) = |
1 |
W ф( p)Wнп ( p) | p =q / T |
; |
|
|
T |
|
|
|||
|
п |
|
|
|
|
|
п |
|
|
|
|
|
|
и применение |
|
- |
|
Переход далее к решетчатым функциям |
Z |
||||
|
|
|
|
|
|
преобразования дает окончательную схему, представленную на рис.
11.8, б. Здесь X 0 ( z) ,
X
(z)
,
X вых
(z)
– дискретные изображения
Лапласа решетчатых исходные непрерывные
рис. 11.5, в; |
|
Wпр (z) = |
функций, функции
X |
|
(z) / |
|
вых |
|||
|
|
|
огибающими которых являются |
||||
x0 (t) |
, |
x(t) , xвых (t) , |
показанные на |
||
X |
|
(z) |
|
– дискретная |
передаточная |
|
|
||||
функция, соответствующая передаточной функции
W |
( p) |
пр |
|
.
Переход
изображения
непрерывной
от |
X (q) |
к |
X (z) |
– это определение дискретного |
|||
X (z) решетчатой |
функции |
x[n], соответствующей |
|||||
функции |
|
|
|
|
изображением Лапласа |
||
|
x(t |
) , обычным |
|||||
которой является X (q) . Эта операция в общем виде состоит из двух этапов. Сначала по изображению X (q) определяют оригинал x(t ) , а затем после замены этой непрерывной функции времени на
291
соответствующую ей решетчатую функцию
дискретное изображение |
X |
|
(z) |
последней. |
|
x[n]
При
находят искомое этом пользуются
таблицами непрерывного и дискретного преобразований Лапласа. Поскольку обычно X (q) представляет собой рациональную дробь, не
содержащуюся в таблице изображений Лапласа, ее предварительно разлагают на простые дроби. Соответственно дискретное
изображение
X |
|
(z) |
|
тоже получается в виде суммы простых дробей.
В частности, |
например, |
если рациональная |
|||
X (q) = G(q) / H (q) не |
имеет кратных полюсов, она может |
||||
представлена в виде: |
|
|
|
|
|
|
|
C |
|
|
|
|
X (q) = |
i |
, |
|
|
|
q − q |
|
|
||
|
i |
i |
|
|
|
|
|
|
|
||
где qi – нули многочлена H (q) , а Ci |
|
|
|
||
= G(qi ) / H |
(qi ) . |
||||
Оригинал |
|
|
|
|
|
|
−1 |
|
|
q t |
. |
x(t ) = L [ X (q)] = Cie |
i |
||||
|
|
|
|
|
|
|
|
|
i |
|
|
дробь
быть
(11.4)
Соответствующая решетчатая функция
x[n] = Cie |
q n |
|
i |
||
|
||
i |
|
.
Совершая прямое дискретное преобразование Лапласа и пользуясь таблицей дискретных изображений Лапласа, находим:
|
|
|
qi n |
|
|
C |
z |
|
X |
(z) = Z Cie |
|
= |
i |
|
|
||
|
|
|
q |
|
||||
|
|
i |
|
|
i |
|
|
|
|
|
|
z − e |
i |
||||
|
|
|
|
|
|
|
|
|
.
(11.5)
Выражение (11.5) представляет собой нахождения X (z) непосредственно по X (q)
общую формулу для в виде рациональной
дроби при отсутствии у последней кратных полюсов. Аналогичная формула существует и при наличии кратных полюсов.
Дискретная передаточная функция |
|
(z) |
находится |
|
Wпр |
||||
соответствующей непрерывной передаточной |
функции |
Wпр |
||
аналогичным образом путем предварительного |
разложения |
ее |
||
по
(q)
на
простые дроби. Передаточная функция Wпр (z) называется дискретной передаточной функцией разомкнутой системы. Как показано на рис. 11.8. б, она связывает дискретное изображение X вых (z) на выходе
292

разомкнутой системы с дискретным изображением
X |
|
(z) |
|
на выходе
импульсного элемента.
Для пояснения понятия дискретной передаточной функции выразим дискретную передаточную функцию разомкнутой системы через весовую функцию приведенной непрерывной части системы.
Сигнал в виде последовательности идеальных импульсов, поступающий на вход приведенной непрерывной части системы с выхода идеального импульсного элемента, можно представить в следующем виде:
где
δ(t − n) = 0
x(t ) δ(t − n) ,
n=0
при t n .
Реакция на выходе приведенной непрерывной части на один такой импульс, поступающий в момент времени t = m , равна
|
|
|
|
w(t |
− m)k |
и |
x[m] |
, |
|
|
|
|
|
|
|
|
|
||||
где |
x[m] |
– значение |
x(t ) |
при |
t = m |
, a |
w(t − m) |
– весовая функция |
||
приведенной непрерывной части системы, равная нулю при t m.
На основании принципа суперпозиции реакция приведенной разомкнутой системы на последовательность импульсов с выхода идеального импульсного элемента равна сумме реакций на каждый импульс, т.е.
n
xвых (t ) = w(t − m)x[m] .
m=0
Перейдем к решетчатым функциям:
x |
[n] = |
вых |
|
n w(n
m=0
−
m)x[m]
.
Подвергнув это уравнение
Z
-преобразованию, получим:
|
|
n |
|
Z{x |
[n]} = Z{ |
|
w(n − m)x[m]} = |
вых |
|
|
|
|
m=0 |
||
Z{w[n]}Z{x[n]}
.
Здесь применена теорема свертки, аналогичная одноименной теореме для непрерывного преобразования Лапласа. Окончательный вид этого равенства:
X вых (z) = W (z) X (z) ,
где
293

|
|
|
X |
|
|
|
(z) |
|
−n |
|
W |
(z) = |
вых |
= Z{w[n]} = w[n] z |
|||||||
|
|
|||||||||
|
X |
|
(z) |
|
||||||
|
|
|
n =0 |
|
||||||
|
|
|
|
|
||||||
(11.6)
Последнее выражение можно рассматривать как одно из определений дискретной передаточной функции, аналогичное подобному определению передаточной функции через весовую функцию в непрерывных системах: дискретная передаточная функция разомкнутой системы, состоящей из идеального импульсного элемента и непрерывной части с весовой функцией w(t) , равна Z -npeобразованию решетчатой весовой функции w(n) ,
соответствующей исходной весовой функции
w(t)
непрерывной
части системы.
Из (11.6) непосредственно следует указанный выше общий порядок нахождения выражения для дискретной передаточной функции через передаточную функцию приведенной непрерывной части: по W (q) находят оригинал w(t ) , затем осуществляют переход
к решетчатой функции |
w(n) |
и далее находят |
преобразование этой решетчатой функции.
W |
|
(z) |
|
как
Z
-
Пример 11.1. Рассмотрим, например, импульсную систему,
состоящую из |
|
непрерывной |
части |
с |
|
передаточной |
функцией |
|||||||||||||
Wнп ( p) = |
k |
|
|
и |
импульсного |
элемента, |
|
генерирующего |
||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
p(Tp +1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
достаточно короткие по сравнению с постоянной времени T |
||||||||||||||||||||
непрерывной части системы импульсы. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Решение. |
|
|
В |
этом |
случае |
передаточную |
функцию |
|||||||||||||
формирователя, |
|
согласно (11.2), можно |
представить |
|
в виде |
|||||||||||||||
Wф ( p) = kиTи . Следовательно, |
передаточная |
функция приведенной |
||||||||||||||||||
непрерывной части |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Wпр ( p) = |
kk |
иTи |
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
p(Tp +1) |
|
|
|
|
|
|
|
|
||||
Переходя к изображению Лапласа и относительному времени, |
||||||||||||||||||||
получаем выражение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Wпр (q) = |
1 |
|
Wпр ( p) | p =q / T |
= |
|
kkиTи |
|
|
|
|
= |
kkиTи |
|
, |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Tп |
|
|
п |
Tп p(Tp +1) p =q / Tп |
|
q(T q +1) |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||
где T = T /Tп .
294
Выражение для дискретной передаточной функции найдем сразу, минуя промежуточные этапы, по окончательной формуле (11.5). В данном случае знаменатель Wпр (q) имеет два нуля: q1 = 0 и
q2 = 1/T , поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
W |
|
(z) = |
C z |
|
+ |
C |
2 |
z |
|
|||||||
|
|
|
|
|
|
|
|
|
1 |
|
q |
|
|
q |
|
|||||||
|
|
|
|
|
|
|
пр |
|
z − e |
|
|
z − e |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kk |
T |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Ci = |
|
и |
|
и |
|
|
, |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
2T q + |
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
q =q |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
т. е. |
1 |
|
2 |
|
и |
и . |
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
C |
= −C |
|
= kk |
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
W |
|
|
(z) = kk T |
|
|
z |
− |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
пр |
|
|
и |
и |
z −1 |
z − |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
,
z |
|
e |
−1/ T |
|
|
.
Изображенная на рис. 11.8, б структурная схема является окончательным математическим описанием импульсной САУ. По этой схеме может быть получена искомая передаточная функция замкнутой системы, связывающая выходную величину системы c входным воздействием:
|
|
|
(z) . |
X вых (z) = Ф |
|
(z) X 0 |
Здесь дискретная передаточная функция замкнутой системы
Ф (z) = |
|
W |
(z) |
||
|
пр |
|
. |
||
|
|
|
|
|
|
|
1 +W |
|
(z) |
||
|
|
пр |
|
|
|
(11.7)
(11.8)
Выражение (11.8) аналогично выражению для передаточной функции замкнутой системы непрерывного действия.
Выше при математическом описании импульсной системы мы предварительно сводили ее к системе с идеальным импульсным элементом путем разложения реального импульсного элемента на идеальный импульсный элемент и формирующий элемент. В качестве идеального импульсного элемента был принят импульсный элемент с мгновенными импульсами типа -импульсов, площадь которых является мерой сигнала на входе импульсного элемента.
Иногда более просто применить идеальный импульсный элемент с прямоугольными импульсами конечной ширины. Это особенно удобно, когда выходные импульсы реального импульсного элемента с достаточной точностью могут быть заменены идеально
295

прямоугольными. В этом случае не потребуется усложнять непрерывную часть системы введением формирующего элемента, преобразующего идеальные импульсы в реальные.
Пример 11.2. Выведем выражение для дискретной передаточной функции импульсной системы с импульсным элементом, выходные импульсы которого имеют прямоугольную форму, ширину Tи и высоту, согласно (12.1), равную kи x , без
перехода к мгновенным импульсам.
Решение. Такой прямоугольный импульс единичной высоты можно представить в виде разности двух сдвинутых ступенчатых функций:
где
γ = T |
/ T |
и |
п |
1(t ) −1(t − γ) ,
– относительная ширина импульса.
Соответственно реакция непрерывной части системы на такой импульс, поступающий в момент t = m ,
|
|
|
|
|
|
|
|
|
|
|
|
wи (t |
− m) = h(t − m) − h(t − m − γ) , |
(11.9) |
|||||
где через |
h |
обозначена переходная функция |
приведенной |
||||||
непрерывной части системы, т.е. ее реакция на единичное ступенчатое воздействие. (Здесь, как всегда, положено, что функции wи и h не существуют при t 0.)
Действуя далее, как при выводе выражения (11.6), получаем:
|
|
|
n |
|
|
x |
вых |
(t ) = |
|
w |
(t |
|
|
и |
|
||
|
|
|
m =0 |
|
|
−
m)kи
x[m]
,
(11.10)
Следовательно,
|
|
|
n |
|
|
xвых (n) = kи wи (n − m)x[m]. |
|
Применив |
|
|
m =0 |
Z |
-преобразование, получим: |
||
|
|
|
|
|
|
Z{xвых [n]} = Z{kи wи [n]}Z{x[n]}, |
|
т. е. |
|
|
|
|
|
X вых |
(z) = W (z) X (z) , |
где |
|
|
|
W (z) = Z{kи wи [n]} = kи wи [n] z −n
n =0
– искомое выражение для дискретной передаточной разомкнутой импульсной системы.
(11.11)
(11.12)
функции
296
Передаточная функция замкнутой системы находится дальше обычным образом исходя из структурной схемы системы.
Итак, мы показали; что импульсная система с линейной непрерывной частью и импульсным элементом с АИМ, имеющим линейную статическую характеристику, описывается линейными уравнениями, т. е. является линейной системой, и вывели соответствующее выражение для ее дискретной передаточной функции.
11.3.2. Частотные характеристики линейных систем автоматического управления с АИМ. Как и системы непрерывного действия, импульсные САУ могут описываться не только передаточными функциями, но и с помощью частотных характеристик. Последние могут быть получены по передаточным функциям или экспериментально.
Выражение для амплитудно-фазовой частотной характеристики получается подстановкой в передаточную функцию q = jω , т. е.
z = e |
jω |
|
, где
ω = Tω
– относительная частота. Соответственно
W |
|
(e |
jω |
) |
– |
это |
амплитудно-фазовая |
|||||
|
|
|||||||||||
разомкнутой, |
а |
Ф |
|
(e |
jω |
) |
– такая же |
|||||
|
|
|||||||||||
частотная характеристика характеристика замкнутой
импульсной САУ. Модуль этих комплексных величин представляет амплитудные, а аргумент – фазовые частотные характеристики.
Особенностью частотных характеристик импульсных систем является то, что они представляют собой периодические функции частоты. Это иллюстрируется рис. 11.9, где показаны амплитудные частотные характеристики непрерывной системы (рис. 11.9, а) и импульсной системы с той же непрерывной частью и идеальным импульсным элементом для двух значений частоты повторения импульсов ωп (рис. 11.9, б и в). Здесь ωнп – полоса пропускания
непрерывной части системы. Частотные характеристики импульсной системы представляют собой бесконечно повторяющуюся с частотой ωп частотную характеристику непрерывной части системы.
Формально периодичность частотной характеристики импульсной системы объясняется тем, что в дискретную передаточную функцию комплексная переменная q входит в виде
297
