
Поставим задачу: найти параметры установившихся вынужденных колебаний на выходе звена, их амплитуду и фазу, если известно уравнение звена и входное воздействие. Для этого подставим в (3.11) выражения (3.10) для u(t) и y(t). Полученное таким образом уравнение определяет искомые значения амплитуды
и фазы y(t). При |
подстановке |
учтем |
следующие |
очевидные |
||||||
выражения для k-й производной от |
u(t) и y(t): |
|
||||||||
|
pk (umaxejωt) ( jω)k umaxejωt; |
|
||||||||
|
pk (ymaxej(ωt )) ( jω)k ymaxej(ωt ). |
|
||||||||
Так как слева и справа в уравнении (3.11) стоят суммы |
||||||||||
производных, то в результате подстановки (3.10) в (3.11) получим: |
||||||||||
|
Q( jω)ymaxej(ωt ) R( jω)umaxejωt. |
|
||||||||
Отсюда |
|
R( jω) |
|
ymax |
|
|
|
|||
|
|
|
|
ej . |
|
|
||||
|
|
|
|
|
|
|
|
|||
Но |
|
Q( jω) |
|
xmax |
|
|
||||
|
|
|
ymax |
|
|
|
|
|||
|
R( jω) |
W( jω); |
|
A(ω); |
(ω), |
|
||||
|
Q( jω) |
umax |
|
|||||||
|
|
|
|
|
|
|
||||
поэтому окончательно имеем: |
|
|
|
|
|
|
||||
|
|
W( jω) A(ω)ej (ω). |
(3.12) |
|||||||
Формула (3.11) определяет искомую связь передаточной функции с частотными характеристиками звена, указанную выше: модуль частотной функции W( jω) есть A(ω), а аргумент – (ω).
Если |
представить |
W( jω)не в показательной, |
как в (3.12), |
|
а в алгебраической форме, т. е. |
|
|
||
|
U(ω) и V(ω) |
W( jω) U(ω) jV(ω), |
(3.13) |
|
то здесь |
будут введенными ранее |
действительной |
||
и мнимой |
частотными |
характеристиками, |
являющимися |
|
координатами амплитудно-фазовой характеристики в комплексной плоскости.
Согласно (3.12) и (3.13) связь между приведенными выше частотными характеристиками следующая:
64

A(ω) |
U |
2 |
(ω) V |
2 |
(ω); |
|
||
|
|
|
||||||
(ω) arctg |
V(ω) |
, |
|
|
|
|||
|
|
|
|
|||||
U(ω) |
|
|
||||||
|
|
|
|
|
|
|
|
|
или
U(ω) A(ω)cos (ω);
V(ω) A(ω)sin (ω).
Порядок получения выражения для перечисленных выше частотных характеристик по передаточной функции звена несложен. Полученное выше выражение для амплитудно-фазовой частотной характеристики формально может быть выведено и непосредственно из определения передаточной функции, согласно (3.7), как отношение изображений Лапласа выходной и входной величин. Если перейти в (3.7) от изображения Лапласа к изображению Фурье, получим:
Y( jω) W( jω)U( jω), |
(3.14) |
где U( jω) и Y( jω) – частотные характеристики входной и выходной величин, т. е. представления их в виде частотных спектров.
На основании (3.14) амплитудно-фазовую частотную характеристику W( jω) можно определить в более общем виде как отношение изображений Фурье выходной и входной величин при нулевых начальных условиях.
Рассмотрим связь между частотными и переходными характеристиками. Наиболее просто она определяется для весовой функции. Если в (3.8) и (3.9) перейти от преобразования Лапласа к преобразованию Фурье, получим соответственно выражения:
W( jω) w(t)e jωtdt; |
(3.15) |
|||
|
|
0 |
|
|
|
1 |
|
|
|
w(t) |
W( j )ejωtdω. |
(3.16) |
||
2π |
||||
|
|
|
||
Первое выражение определяет частотные характеристики звена по его весовой функции, а второе, наоборот, – весовую функцию по амплитудно-фазовой характеристике.
По частотным характеристикам звена можно непосредственно определить его реакцию не только на импульсное воздействие, но и на входное воздействие любого вида.
65

3.3. Особенности частотных характеристик минимально-фазовых звеньев
В общем случае исчерпывающее описание звена с помощью частотных характеристик требует знания амплитудно-фазовой частотной характеристики W( jω) либо, согласно (3.12) и (3.13), любой пары характеристик: A(ω) и (ω) или U(ω) и V(ω). Однако оказывается, что для некоторого класса звеньев существует однозначная связь между образующими эти пары функциями. Поэтому для полного описания таких звеньев достаточно иметь только одну из них.
Остановимся |
вначале на связи между действительной |
U(ω) |
и мнимой V(ω) |
частотными характеристиками. Доказано, |
что |
в случае устойчивых звеньев эти функции однозначно связаны, т. е. по любой из них можно найти другую. Устойчивым звеном называется звено, все полюсы передаточной функции которого, т. е. нули ее знаменателя Q(p) или корни уравнения Q(p) 0, имеют отрицательные действительные части. Таким образом, устойчивые звенья полностью описываются любой из двух характеристик: U(ω) или V(ω).
Теперь обратимся к определению связи между амплитудной A(ω) и фазовой (ω) частотными характеристиками. Доказано, что эти функции однозначно связаны у минимально-фазовых звеньев. Минимально-фазовым звеном называется звено, у которого все полюсы и нули передаточной функции имеют отрицательные или равные нулю действительные части. Свое название минимальнофазовые звенья получили в связи с тем, что они дают минимальный фазовый сдвиг при любом значении частоты ω по сравнению с любыми другими звеньями, имеющими такую же амплитудную
характеристику |
A(ω), но у которых указанное выше условие |
в отношении |
полюсов и нулей передаточной функции не |
выполняется. Чтобы проиллюстрировать последнее, рассмотрим звено с передаточной функцией
W (p) k . |
|
1 |
Tp 1 |
|
|
66
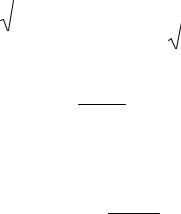
Согласно определению это звено является минимальнофазовым, так как его единственный полюс равен 1/T , т. е. отрицательный действительный, а нулей вообще нет. Амплитуднофазовая характеристика этого звена
W ( jω) |
k |
|
k jkTω |
|
, |
|
|
||||
|
|
|
|
|
|||||||
1 |
1 jTω |
1 T |
2ω2 |
|
|
|
|||||
|
|
|
|
||||||||
и, следовательно, амплитудная характеристика |
|
|
|
||||||||
|
|
|
|
k |
|
|
|
||||
A (ω) |
U2(ω) V2(ω) |
|
|
, |
|||||||
|
|
|
|
|
|||||||
1 |
|
|
|
|
|
|
1 T |
2ω2 |
|||
|
|
|
|
|
|
|
|||||
а фазовая
1(ω) arctgV(ω) arctgTω.
При ω значение фазы 1(ω) изменяется от 0 до π/2. Возьмем теперь звено с передаточной функцией
W (p) k . |
|
2 |
Tp 1 |
|
|
Это звено не является минимально-фазовым, так как его передаточная функция имеет положительный действительный полюс
1/T (заметим, что по этой причине данное звено является также
инеустойчивым). Амплитудно-фазовая характеристика этого звена
W ( jω) |
k |
|
k jkTω |
. |
|
|
|||
2 |
1 jTω |
|
1 T2ω2 |
|
|
|
|||
Соответственно его амплитудная характеристика совпадает |
||||
с амплитудной характеристикой первого звена, т. е. A2(ω) A1(ω), |
||||
а фазовая характеристика |
2(ω) arctgTω π [ 1(ω) π]. При |
|||
значение 2(ω) изменяется от π до π/2. Таким образом, второе звено создает большее фазовое запаздывание, чем первое – минимально-фазовое.
Для графического описания минимально-фазовых звеньев применяют амплитудную частотную характеристику. В случае необходимости по ней может быть построена фазовая характеристика. Принципиально связь между этими характеристиками такова, что величина фазы растет с увеличением наклона амплитудной характеристики. При этом в случае применения логарифмической амплитудной характеристики можно приближенно считать, что участку ЛАХ с наклоном 20 дБ/дек соответствует
67
фазовый сдвиг, близкий к π/2, а участку ЛАХ с наклоном 40 дБ/дек – сдвиг π.
3.4. Логарифмические частотные характеристики
При исследовании систем автоматического управления амплитудную и фазовую частотные характеристики удобно строить в логарифмических координатах. Это связано с двумя обстоятельствами.
Во-первых, в логарифмических координатах характеристики деформируются таким образом, что возникает возможность в подавляющем большинстве практических случаев упрощенно изображать амплитудные частотные характеристики ломаными линиями.
Второе удобство связано с построением амплитудных частотных характеристик цепочки последовательно соединенных звеньев. Из самого определения амплитудных частотных характеристик следует, что амплитудная частотная характеристика цепочки звеньев равна произведению амплитудных частотных характеристик составляющих ее звеньев, т. е.
n |
|
A(ω) Ai(ω), |
(3.17) |
i 1
где n – число последовательно соединенных звеньев. Если прологарифмировать (3.17), получим:
n
lg A(ω) lg Ai(ω),
i 1
т. е. в логарифмическом масштабе амплитудная частотная характеристика цепочки звеньев равна сумме амплитудных характеристик отдельных звеньев.
Амплитудная частотная характеристика в логарифмических координатах строится в виде зависимости L(ω) 20lg A(ω) от lgω, называемой логарифмической амплитудной характеристикой (ЛАХ), а фазовая – в виде зависимости (ω) от lgω, называемой логарифмической фазовой характеристикой (ЛФХ).
В качестве единицы L(ω) используется децибел, равный одной десятой бела. Бел – это единица десятичного логарифма коэффициента усиления мощности сигнала, т. е. 1 бел соответствует
68
усилению мощности в 10 раз, 2 бела – в 100 раз, 3 бела – в 1000 раз и т. д. Так как мощность сигнала пропорциональна квадрату
амплитуды, a lg A2(ω) 2lg A(ω), то усиление в белах, выраженное через отношение амплитуд A(ω), равно 2lg A(ω). Соответственно в децибелах оно равно 20lg A(ω). При этом существуют следующие соотношения между значениями A(ω) и L(ω) (табл. 3.1).
|
|
|
|
|
|
|
Таблица 3.1 |
|
|
|
|
|
|
|
|
|
|
A(ω) |
0,001 |
0,01 |
0,1 |
1 |
10 |
100 |
1000 |
|
|
|
|
|
|
|
|
|
|
L(ω), дБ |
–60 |
–40 |
–20 |
0 |
20 |
40 |
60 |
|
|
|
|
|
|
|
|
|
|
При применении ЛАХ логарифмическая фазовая характеристика строится в полулогарифмических координатах, т. е. в виде зависимости (ω) от lgω, чтобы обе характеристики были связаны одним масштабом на оси абсцисс. Использование логарифмического масштаба на оси ординат фазовой характеристики не имеет смысла, так как фазовый сдвиг цепочки звеньев и так получается просто в виде суммы фазовых сдвигов на отдельных ее звеньях.
На оси абсцисс указываются либо прямо значения lgω, либо, что практически более удобно, значения самой частоты ω. В первом случае единицей приращения lgω является декада, соответствующая изменению частоты в 10 раз. Применяется также деление оси абсцисс на октавы. Октава соответствует изменению частоты в два раза. Одна октава равна 0,303 декады, так как lg2 0,303.
Так как при использовании логарифмического масштаба точка, соответствующая ω 0, находится слева в бесконечности, логарифмические характеристики строятся не от нулевой частоты, а от достаточно малого, но конечного значения ω, которое и откладывается в точке пересечения координатных осей.
Например, характеристики инерционного звена первого порядка с передаточной функцией W(s) k /(Ts 1) приведены на рис. 3.7.
69
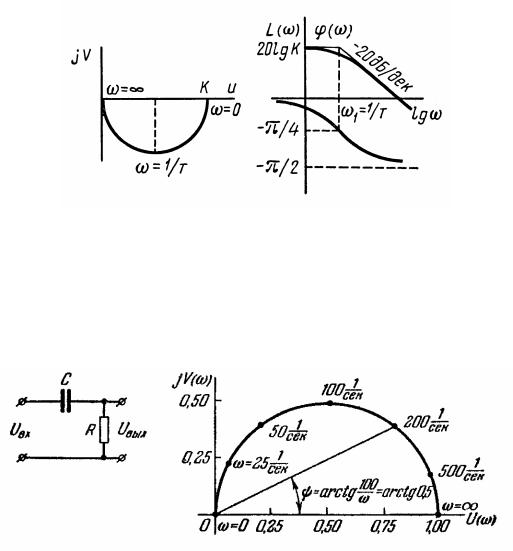
а б
Рис. 3.7. Характеристики инерционного звена первого порядка
Пример 3.3. Построить амплитудно-фазовую характеристику цепи RC, представленной на рис. 3.8, а, где R 1 кОм, C 10 мкФ.
а |
б |
||||
Рис. 3.8 |
|
||||
Решение. Передаточная функция цепи, согласно примеру 2.3, |
|||||
равна |
|
||||
W(p) |
Tp |
. |
|
|
|
|
|
||||
|
Tp 1 |
|
|||
Тогда АФЧХ имеет вид |
|
||||
W( jω) |
jωT |
|
, |
||
|
|||||
|
|
jωT 1 |
|
||
где T RC 103 10 5 10 2 с.
Преобразуем полученное выражение АФЧХ таким образом, чтобы оно представляло собой комплексное число в алгебраической форме:
70

W(jω) U(ω) jV(ω) |
|
ω2T2 |
|
|
j |
ωT |
, |
|||||
|
2 |
2 |
2 2 |
|||||||||
т. е. |
|
|
1 ω T |
|
|
1 ω |
T |
|||||
|
|
|
|
|
|
|
|
|
|
|
||
U(ω) |
ω2T2 |
|
; |
V(ω) |
|
|
ωT |
. |
|
|
||
2 |
2 |
|
|
2 2 |
|
|
||||||
1 ω T |
|
|
|
|
1 ω |
T |
|
|
||||
Задаваясь отдельными значениями частоты ω, можно по формулам вычислить ряд значений U(ω) и V(ω), и построить по ним АФЧХ цепи. Например, для предельных значений частоты можно получить следующую табл. 3.2.
|
|
|
Таблица 3.2 |
|
|
|
|
ω |
U(ω) |
V(ω) |
|
0 |
0 |
0 |
|
1/T |
0,5 |
0,5 |
|
|
1 |
0 |
|
Однако анализ выражений U(ω) |
и V(ω) |
показывает, что для |
|
АФЧХ может быть получено аналитическое выражение. |
|||
Пусть ωT a, тогда |
U(ω) a2 |
/(1 a2) |
и V(ω) a/(1 a2). |
Следовательно, U(ω)/V(ω) a, отсюда U(ω) U2(ω)/[U2(ω) V2(ω)]
или U2(ω) V2(ω) U(ω). Тогда
V(ω) [U(ω) 0,5]2 0,52.
Для положительных частот АФЧХ является полуокружностью, расположенной в верхней полуплоскости с центром в точке (0,5; j0) и радиусом 0,5 (см. рис. 3.8, б).
Из полученных выражений видно, что при ω 0 W( jω) 0 j0, а при ω W( jω) 1 j0. Частоты, соответствующие промежуточным точкам кривой, могут быть найдены следующим образом. Аргумент комплексного числа
(ω) argW( jω) V(ω) argtg 1 argtg100, U(ω) T
поэтому луч, проведенный из начала координат под углом (ω) к оси абсцисс, пересекает АФЧХ в точке, в которой величина ω определяется через (ω) последним выражением. Например, для
(ω) 45 частота ω 1/T 100 1/с.
71
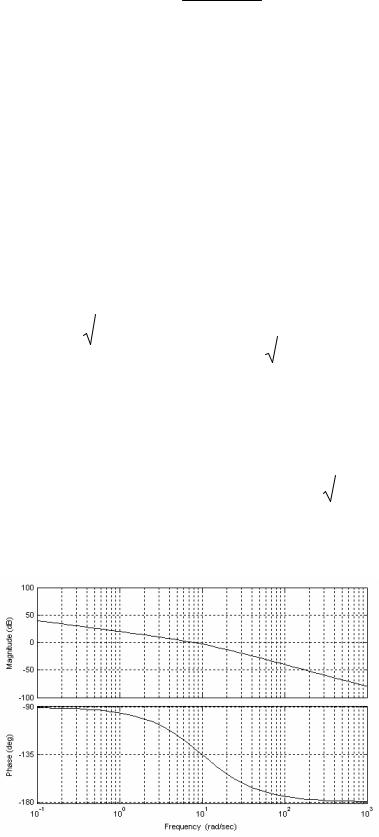
Пример 3.4. Передаточная функция динамического звена
W(p) k . p(Tp 1)
Вывести аналитические выражения и построить логарифмические амплитудную и фазовую частотные характеристики звена при k 10с 1, T 10 1 c.
Решение. АФЧХ звена
W(jω) |
|
k |
|
|
kTω |
|
j |
|
|
|
k |
|
|
, |
||||||||||
|
|
|
|
ω(1 T2ω2) |
|
|
|
|
|
|
|
|||||||||||||
|
jω(jωT 1) |
|
|
|
|
ω(1 T2ω2) |
||||||||||||||||||
т. е. |
|
|
kT |
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|||
U(ω) |
|
|
; |
|
V(ω) |
|
|
|
|
|
|
|
. |
|
|
|||||||||
1 T2ω2 |
ω(1 T2ω2) |
|
||||||||||||||||||||||
АЧХ звена |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A(ω) |
|
|
U2(ω) V2(ω) |
|
|
|
|
|
|
. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ФЧХ звена |
|
|
|
|
|
|
|
|
|
ω 1 T2ω2 |
|
|
|
|||||||||||
|
|
|
|
|
V(ω) |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
(ω) arctg |
arctg |
. |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Тогда ЛАХ звена |
|
|
|
|
U(ω) |
Tω |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
. |
||||||||||||||||||||||
L(ω) 20lg A(ω) 20lgk 20lgω 20lg |
1 T2ω2 |
|||||||||||||||||||||||
Логарифмические |
частотные характеристики, |
построенные |
||||||||||||||||||||||
в пакете Control системы Matlab, представлены на рис. 3.9.
Рис. 3.9
72
3.5. Преобразование случайного сигнала линейным звеном
Стационарные случайные воздействия u(t) вызывают соответственно стационарные случайные изменения выходной величины y(t) звена или системы автоматического управления, если они, разумеется, тоже стационарны. Найдем связь между характеристиками процессов u(t) и y(t) на входе и выходе звена.
В общем случае случайное воздействие u(t) состоит из среднего значения mu(t) и центрированной случайной части u0(t), т. е.
u(t) mu(t) u0(t).
Соответственно может быть представлена и выходная величина звена:
y(t) my(t) y0(t).
Для линейного звена на основании принципа суперпозиции каждая из этих двух составляющих y(t) может быть определена порознь: my(t) – как реакция на mu(t), a y0(t) – как реакция на u0(t).
Средние значения mu(t) и my(t) являются неслучайными
величинами и связаны через передаточную функцию: |
|
|
|
my(t) W(p)mu(t). |
(3.18) |
В частности, для |
стационарного случайного процесса |
mu(t) |
и соответственно my(t) |
представляют собой постоянные величины. |
|
Поэтому связь между ними определяется по уравнению статики, т. е.
|
|
|
|
my W(0)mu . |
|
(3.19) |
Перейдем теперь к определению центрированной стационарной |
||||||
случайной величины y0(t) по u0(t). |
|
|
||||
Входное воздействие u0(t) может быть задано либо |
||||||
корреляционной |
функцией |
Ru(τ), либо |
спектральной |
плотностью |
||
мощности |
Su(ω). Эти |
характеристики |
могут быть |
получены, |
||
в частности, |
в |
результате |
обработки экспериментально снятых |
|||
кривых u(t). |
|
|
|
|
|
|
Выходная величина |
y0(t) также может быть охарактеризована |
|||||
функциями Ry(τ) или Sy(ω). |
|
|
|
|||
|
|
|
|
|
|
73 |
