
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
4.2 ] |
Магнитные поля простейших токовых конфигураций |
251 |
Используя теорему Стокса для вывода теоремы о циркуляции в форме (4.12), мы, между прочим, доказали еще одно важное ее свойство: несущественно, каким именно образом линии тока пересекают контур — они могут пересекать его под любым углом, быть может, «вперед–назад», образуя токовые петли и т. д. Все это учитывается интегралом и никак не сказывается на формуле (4.10). В нее входит только заряд, в единицу времени пересекающий любую поверхность, натянутую на контур, а как это происходит — не имеет значения.
Поскольку уравнения (4.3), (4.10), (4.12) линейны, для век-
тора напряженности магнитного поля справедлив принцип суперпозиции — поле суммы токов равно сумме полей каждого
из них. Это справедливо и для действующего поля , но лишь в вакууме или в линейной среде. Например, в ферромагнетиках принцип суперпозиции не работает — и не только для , но и для , ввиду нетривиальности граничных условий.
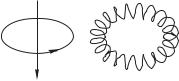
В качестве примера вычисления магнитного поля с помощью теоремы о циркуляции рассмотрим длинный цилиндрический соленоид, по обмотке которого протекает ток : (рис. 4.2). В отличие от тонкого кольца с током, поле внутри соленоида оказывается практически одномерным и параллельным его оси. Это следует из симметрии задачи, но может быть прямо выведено из закона Био и Савара при следующих условиях:
а) диаметр катушки должен H 
быть много меньше ее длины; |
A |
l |
x |
|
б) шаг намотки должен быть |
||||
|
|
|||
|
|
|
||
много меньше диаметра соленоида; |
|
Рис. 4.2 |
|
|
в) намотка должна быть плот- |
|
|
||
|
|
|
ной, т. е. диаметр провода должен быть равен шагу намотки, в противном случае мы правильно определяем поле только для расстояний от стенок соленоида, много б´ольших зазора между витками.
Иногда об этих условиях забывают. Другим примером «забывчивости» является популярное, но неправильное утверждение о том, что поле вне такого соленоида равно нулю. На самом деле оно такое же, как и у прямого провода:
G 2 + ,
где — расстояние от оси (превышающее радиус катушки). Это следует из аксиальной симметрии задачи и теоремы о циркуляции. В самом деле, как уже говорилось выше, току безразлично, каким образом пересекать натянутую на контур интегрирования поверхность, важно лишь, что он пересекает ее один раз. Для
252 |
Магнитное поле тока |
[ Гл. 4 |
дальнейшего существенно, что силовые линии лежат в плоскости, перпендикулярной оси системы.
Определим поле внутри соленоида. Проведем любую плоскость через его ось и построим в этой плоскости прямоугольный контур , как показано на рисунке. Одна из длинных сторон прямоугольника расположена вне катушки; поле к ней перпендикулярно, и вклад ее в циркуляцию равен нулю. Две боковых стороны мы с самого начала выбираем малыми и в дальнейшем устремляем к нулю, поэтому их вкладом также можно пренебречь. Остается длинная сторона внутри катушки. Пусть плотность намотки (число витков на единицу длины соленоида) равна . Если ! — полное число витков, а — длина соленоида, то !. Ток : пересекает контур столько раз, сколько витков он захватывает, т. е. . Теорема о циркуляции (4.10) принимает вид простого соотношения
G :,
откуда окончательно следует
G : B :; 10: |
(4.13) |
|
|
Сколь бы ни были подробны наши рассуждения (которые при известном опыте попросту опускаются), довольно очевидно, что вывод этой хрестоматийной формулы оказался намного проще, чем если бы мы пользовались напрямую законом Био и Савара.
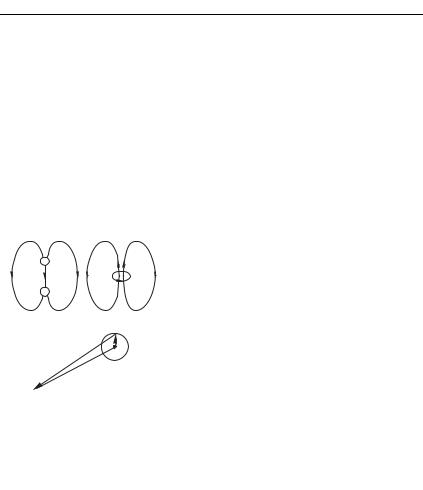
Рассмотрим еще один пример, ответ в котором будет чисто качественным, но принципиально важным для всей физики магнитных полей. Рассмотрим стационарную токовую конфигурацию, изображенную на рис. 4.3, — кольцевой ток, охватывающий
|
|
прямой ток. (Она не является |
|
|
чисто умозрительной — исполь- |
|
|
зуя сверхпроводящую технику, ее, |
|
|
в принципе, можно реально осу- |
I2 |
|
ществить.) Как будут выглядеть |
|
магнитные силовые линии? |
|
I1 |
|
Для прямого тока ответ изве- |
|
Рис. 4.3 |
стен — это будут концентрические |
|
окружности, центры которых ле- |
|
|
|
жат на оси. Силовые линии витка с током лежат, как известно, в плоскости, проходящей через ось. Это замкнутые линии неправильной формы, охватывающие виток, — картина, хорошо известная из школьного курса физики. (Лишь одна из них незамкнута и совпадает с осью; для нас она в данном случае неинтересна.) При попытке сложить эти два поля, следуя принципу суперпозиции, окажется, что результирующая силовая линия навивается на некоторую тороидальную поверхность и целиком на
4.3 ] |
Вектор-потенциал |
253 |
ней расположена. Первое впечатление — это замкнутая на себя спираль.
Заметим, однако, что для замкнутости спирали необходима соизмеримость длины обхода тора и ее шага, т. е. сделав некоторое целое число обходов, силовая линия должна замкнуться сама на себя. Меняя радиус тора, мы получим семейство вложенных тороидальных поверхностей, причем замкнутые силовые линии будут соответствовать счетному подмножеству, а незамкнутые — континууму.
Это и есть «третий вариант» поведения магнитной силовой линии — магнитная поверхность. То есть силовая линия может
не только идти из бесконечности в бесконечность или быть замкнутой, но и занимать некоторую поверхность, плотно ее заштриховывая, и не иметь при этом ни начала, ни конца. Как показано в нашем примере, поверхность эта может быть вложена в конечный объем. Такое поведение силовых линий — вовсе не экзотика; оно, например, используется в прикладных задачах для удержания заряженных частиц.
Ничего подобного нет в электростатике. Это лишнее свидетельство наивности первоначальных попыток построить магнитостатику по образу электростатики. На самом деле электрические и магнитные поля обладают разными геометрическими свойствами, что формально отражено в различных базовых уравнениях:
3 и rot
В заключение данного параграфа дадим определение магнитного потока. Для любой гладкой поверхности 9 магнитный поток
определяется следующим образом:
Это понятие оказывается очень удобным и широко используется
вэлектродинамике. Если поверхность замкнута, то в силу (4.1)
0 — вне зависимости от того, расположены источники маг-
нитного поля снаружи или внутри нее. Единица магнитного потока имеет специальное название — вебер:
1 Вб 1 А с Ом
Такая размерность последует из закона электромагнитной индукции, с которым нам еще предстоит познакомиться.
4.3. Вектор-потенциал
Материал, изложенный в данном параграфе, обычно не принято помещать в курс общей физики. Нам, однако, представляется, что экономия в объеме и сложности ряда последующих

254 |
Магнитное поле тока |
[ Гл. 4 |
вычислительных процедур оказывается столь значительной, что оправдывает такое начинание. (То же самое можно сказать и об операциях векторного дифференцирования. Они позволяют представить уравнения поля в чрезвычайно компактной и наглядной форме, существенно упрощают многие доказательства и выводы, и потому, на наш взгляд, ст´оит как можно раньше преодолеть некоторые трудности, связанные с освоением этого аппарата.)
Мы уже могли оценить, сколь конструктивным оказалось в электростатике понятие электрического потенциала. Определение его было дано в формулах (1.16), (1.17), а основное уравнение, которому потенциал подчиняется как функция точки, — (1.19). Правда, определение давалось для системы дискретных точечных зарядов, а уравнение соответствует описанию зарядового распределения непрерывной функцией 3 . Однако все проблемы снимаются простым обобщением определения (1.16), (1.17):
|
1 |
|
% |
(4.14) |
|
400 |
|||||
|
# |
|
|||
Теперь попробуем подобным же образом ввести функцию, порождающую магнитное поле. Только, в отличие от электростатики, источником будет не скаляр 3, а вектор . Рассмотрим некоторую проводящую среду с распределением плотности тока . Введем вектор с компонентами
, , |
1 |
|
3 , , |
|
(4.15) |
|
4 |
# |
|||||
|
|
|
||||
Сравнивая (4.14), (4.15) и (1.19), нетрудно убедиться, что компоненты вектора должны удовлетворять уравнению Пуассона:
|
2 2 2 2 |
2 2 2 " |
(где , , ), что обычно принято записывать в виде
|
2 |
(4.16) |
|
||
|
|
Векторная величина и называется вектор-потенциалом. Но это название имеет смысл лишь в том случае, если эта функция и в самом деле порождает вектор магнитного поля. Чтобы в этом убедиться, вычислим прежде всего дивергенцию векторпотенциала:
|
1 |
|
|
|
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|
||||
4 |
# |
4 # |
||||||||||
Мы преобразовали последний интеграл по теореме Гаусса. Поскольку объемное интегрирование предполагается по всей проводящей среде, где 0, постольку поверхностный интеграл
4.4 ] |
Магнитный диполь. Понятие о магнитном моменте |
255 |
должен браться по поверхности всех проводников, где, однако, " 0, а потому равен нулю и весь интеграл. Таким образом,
0
Но тогда имеет место следующее соотношение (см. предыдущий параграф):
2 2 ,
так что мы можем заменить левую часть в уравнении Пуассона (4.16) для вектор-потенциала:
Сравнивая этот результат с дифференциальной формой теоремы
о циркуляции (4.12), получаем окончательный результат: |
|
|
(4.17) |
Мы имеем возможность еще раз убедиться в различной векторной природе электрического и магнитного полей. Если стати-
ческое электрическое поле представимо как градиент некоторой скалярной функции (такие поля называют потенциальными),
то магнитное поле в вакууме есть ротор некоторой векторной функции. Поля такого рода принято называть соленоидальными.
Скалярный электрический потенциал определен, как и потенциальная энергия, с точностью до константы. Произвол в определении вектор-потенциала больше: поскольку ротор градиента любой скалярной функции тождественно равен нулю, то и величина определена с точностью до B, где B — произвольная скалярная функция. Наблюдаемой же (измеряемой) величиной остается поле , т. е. ротор вектор-потенциала. Мы не будем, однако, углубляться в этот вопрос, потому что данное выше определение (4.15)–(4.17) вполне корректно и для целей нашего курса достаточно.
4.4.Магнитный диполь. Понятие
омагнитном моменте
На первый взгляд, из закона Био и Савара (4.3) следует спадание магнитного поля на бесконечности, аналогичное закону Кулона 2 . Для некоторых вырожденных ситуаций мы и в самом деле можем в случае электро- и магнитостатики получить ответы, функционально тождественные. Так, электрическое поле однородно заряженного длинного провода и магнитное поле длинного провода с током, хотя и различаются геометрией, зависят от радиуса по одному закону 1 . Но в общем случае между ними существует принципиальное различие. Если уеди-
256 |
|
|
|
Магнитное поле тока |
[ Гл. 4 |
|
ненный заряд любого знака имеет право на существование, то |
||||||
элемент тока не может существовать сам по себе, ибо любой ста- |
||||||
ционарный ток должен быть замкнут. Потому и мультипольность |
||||||
магнитного поля не может быть ниже дипольного приближения: |
||||||
|
|
G 3 при |
|
|||
(Конечно, на достаточно больших, например галактических, мас- |
||||||
штабах этим качеством обладает и электрическое поле, но это |
||||||
уже следствие нейтральности Вселенной, а не собственно элек- |
||||||
тродинамики.) |
|
|
|
|
|
|
Таким образом, элементарным объектом в физике магнитных |
||||||
полей оказывается диполь, и именно дипольным по геометрии и |
||||||
функциональной зависимости будет поле произвольной системы |
||||||
|
|
|
|
токов на больших расстояниях. |
|
|
E |
|
|
|
B |
По природе и по геометрии сило- |
|
|
|
|
|
|
||
+ |
|
|
|
вых линий электрический и магнит- |
||
_ |
|
|
I |
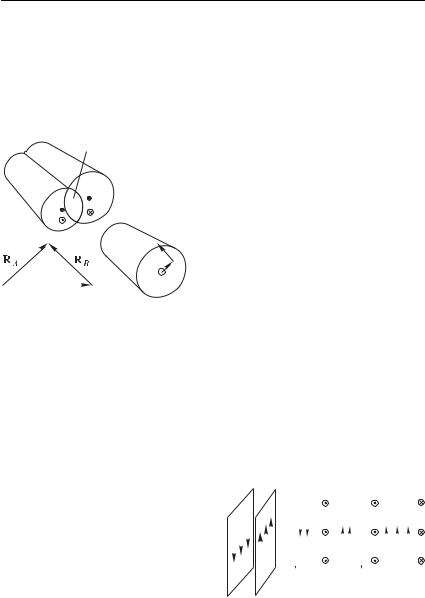
ный диполи различаются (рис. 4.4 а). |
||
|
|
Поэтому перенос результатов |
гл. 1 |
|||
à |
|
|
|
|||
|
|
|
на этот случай невозможен и вы- |
|||
|
|
|
|
|||
|
|
r |
|
вод |
основных соотношений должен |
|
|
|
|
быть проведен заново. Здесь весь- |
|||
R |
|
|
|
|||
|
|
|
ма полезным для нас окажется ма- |
|||
á |
R |
|
|
териал предыдущего параграфа, т. е. |
||
|
|
описание магнитного поля посредст- |
||||
|
|
|
|
|||
Рис. 4.4 |
|
|
вом вектор-потенциала. Рассмотрим |
|||
|
|
квазистационарную токовую систему. |
||||
|
|
|
|
|||
Можно в принципе смотреть на нее как на квазинейтральную |
||||||
систему зарядов, совершающих замкнутое финитное движение |
||||||
(поскольку квазистационарные токи должны быть замкнуты). |
||||||
Обратимся к формуле (4.15) и проведем следующую цепочку |
||||||
замен в подынтегральном выражении: |
|
|||||
|
D |
|
|
Мы выбрали элемент |
столь малым, чтобы в него попали |
||
заряды только одного сорта и чтобы усреднения по объему не требовалось. В то же время усреднение по времени необходимо ввиду дискретности носителей заряда (в сущности, само понятие постоянного либо квазистационарного тока неявно подразумевает такое усреднение). Следуя логике этой замены, мы можем интегрирование в (4.15) заменить суммированием по дискретным зарядам, что в данном случае будет удобнее,
|
1 |
5 , |
(4.18) |
|
4
'
а затем, в соответствии с рис. 4.4 б, представим ' в виде

4.4 ] Магнитный диполь. Понятие о магнитном моменте 257
векторной суммы ' ', где все ' . Тогда
|
1 5 |
1 |
/ |
|
1 |
/ |
|
1 |
|
||||
|
|
|
|
|
|
|
|
||||||
|
4 4 |
' ' 4 |
' ' ' |
|
|||||||||
|
' |
|
|
|
' |
|
|
' |
|
|
|
|
|
Первый член этой разности есть не что иное, как усредненная по времени временн´ая производная полного дипольного момента
системы, |
|
|
|
|
|
|
|
|
/' ' |
|
|
/' ' |
|
||
|
' |
|
' |
||||
Неважно, чему он равен и по какому закону меняется. Важно, что система совершает финитное движение и любая величина, характеризующая ее состояние, изменяется в конечных пределах, а поэтому при усреднении по достаточно большому промежутку времени ее производная стремится к нулю. Пусть — такая величина, а > — характерное время эволюции системы.
Тогда |
|
|
. |
|
0 при > |
|
|
|
|
||
|
|
|
Нам еще не один раз придется воспользоваться этим результатом. Обратимся ко второму члену разности, принимая во внимание, что 1 3:
1 |
|
|
/' ' ' , |
(4.19) |
|||
|
|
|
|
|
|||
4 3 |
|||||||
|
|
|
|
|
' |
|
|
в котором сделаем тождественное преобразование |
|
|
|||||
' ' |
|
' ' ' ' |
|
|
|||
|
|
|
|||||
Первый член в правой части |
— снова полная производная, |
даю- |
|||||
щая нуль при усреднении, поэтому, говоря о средних по времени значениях, можно приравнять левую часть второму члену в правой. Сделаем это в выражении (4.19), введя, соответственно, коэффициент 1 2:
1 |
|
|
|
|
1 |
|
|
|
|
|
/' ' ' ' ' |
|
|
||||
8 3 |
8 3 /' ' ' |
|||||||
' |
|
|
|
' |
(4.20) |
|||
|
|
|
|
|
|
|
|
|
Если определить вектор магнитного момента системы как |
||||||||
|
|
|
1 |
|
, /' ' , |
(4.21) |
||
|
|
2 |
||||||
|
|
|
' |
|
|
|
||
' |
|
|
|
|
||||
то вектор-потенциал магнитного поля |
системы на |
больших, |
||||||
в сравнении с ее размерами, расстояниях, имеет вид |
|
|||||||
|
|
|
|
|
|
|
(4.22) |
|
|
|
|
|
|
4 3 |
|
|
|
9 Основы физики. Т. I

258 |
Магнитное поле тока |
[ Гл. 4 |
||
Эквивалентная форма: |
|
|||
|
|
1 |
, 1 |
(4.23) |
|
4 |
|||
Итак, мы видим, что в теории магнитных полей дипольное приближение базируется на понятии вектор-потенциала — полезно сравнить выражения (1.24) и (4.22). Мы ввели понятие магнитного диполя и теперь можем для удобства считать его «точечным». В этом случае, т. е. при вычислении поля на расстояниях, существенно б´ольших пространственного масштаба токовой конфигурации, последняя характеризуется единственным векторным параметром . Для вычисления поля воспользуемся формулой (4.23). Предварительно проведем операцию векторного дифференцирования в общем виде. Пусть — некоторый постоянный вектор, тогда
rot , ,
В нашем случае 1 , поэтому 2 1 0, потому что это уравнение Пуассона для потенциала точечного заряда при 0 (впрочем, это можно проверить и прямым вычислением). Таким образом,
rot , |
|
|
|
|
|
|
, 3 3 |
, |
|
4 |
3 4 |
4 |
|
||||||
Используя также цепочку преобразований |
|
|
|||||||
|
|
|
, |
|
|||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
||
получаем окончательный ответ: |
|
|
|||||||
rot |
3 2 |
|
(4.24) |
||||||
|
|
||||||||
|
|
4 5 |
|
|
|||||
Этот результат оказался идентичным формуле (1.25), в особенности если мы, имея в виду уже отмеченную перекрестную аналогию, перепишем последнюю для электрической индукции, т. е. просто умножим на <0. Для справки отметим, что мы ввели т. н. амперовский магнитный момент; иногда вместо него используют кулоновский магнитный момент, отличающийся коэффициентом
10 4$.
В отличие от электрического диполя, простейший магнитный диполь представляет собой тонкий замкнутый виток с током (рис. 4.4 а). Для вычисления его дипольного момента построим цепочку, обратную той, которую мы использовали при выводе формулы (4.18):
D 9 |
: , |

4.4 ] Магнитный диполь. Понятие о магнитном моменте 259
где 9 — поперечное сечение провода, : — ток, протекающий через виток. Теперь сумму в (4.21) можно заменить интегралом
по длине контура:
12 , :
Воспользуемся известным свойством векторного произведения: модуль равен удвоенной площади треугольника, постро-
енного на |
векторах и как на сторонах. Таким |
образом, |
, 2 |
, где 9 — площадь контура витка, и окончательно: |
|
|
:9 |
(4.25) |
Здесь — единичный вектор нормали к плоскости витка, ориентированный согласно правилу буравчика по отношению к направлению тока, или, что то же: с конца его ток в контуре должен выглядеть протекающим против часовой стрелки. Если мы имеем дело с катушкой из ! витков, ее магнитный момент равен !:9; подразумевается, что расстояние, на котором определяется поле катушки, или масштаб изменения внешнего поля существенно превышают любой ее размер. Если же магнитный диполь — иной природы, например, постоянный магнит, то его очень часто
удобно представить в виде витка или трубки с азимутальным током. Этот фиктивный ток называют током намагничения.
В качестве источника поля он ведет себя так же, как и реальный ток, не следует только подставлять его в теорему о циркуляции, а тем более в закон Джоуля–Ленца.
Вернемся к дискретному представлению магнитного момента (4.21). Предположим, что диполь формируется циклическим движением одной частицы, либо ансамблем одинаковых частиц, либо, наконец, ансамблем различных частиц, но имеющих одинаковое отношение заряда к массе, которое мы обозначим как D . Опуская, ради простоты записи, индексы и операцию усреднения, имеем
|
1 |
|
/ |
|
< |
|
, |
< |
|
|
2 |
|
2 |
2 |
|||||||
|
|
|
|
|||||||
Поскольку есть момент импульса частицы, наша формула связывает магнитный момент и момент импульса системы:
|
< |
|
(4.26) |
|
2 |
||||
|
|
|
Величина D 2 называется гиромагнитным отношением. Соотношение (4.26) оказывается настолько универсальным, что работает даже в квантовой механике — именно этим коэффициентом оказываются связаны механический и магнитный моменты электронных орбит в атоме. И только при переходе к элементарным частицам появляется необходимость в его модификации.
9*
260 Магнитное поле тока [ Гл. 4
Задачи
1. По двум бесконечно длинным прямолинейным проводникам и , выполненным из немагнитного материала и ограниченным пересекающимися цилиндрическими поверхностями, текут в противоположных направлениях токи одинаковой плотности 3 (рис. 4.5 а). Найти величину и направление
магнитного поля в полости Г.
Решение. Введем в сечении проводников вектор (рис. 4.5 б) и воспользуемся принципом суперпозиции полей. Поскольку плотности тока равны
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в каждом из проводников и противо- |
||||||||
|
à |
|
|
|
|
|
|
|
|
|
|
|
|
положно направлены, дополним мыслен- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
но каждый проводник до цилиндра, так |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что нулевой ток в полости получится |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
как результат сложения встречных то- |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|
|
|
|
|
|
ков. Произвольная точка полости будет |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
à |
|
|
|
|
À |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
характеризоваться радиусами-векторами |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и ; . Внутри ци- |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
линдрического проводника, по которому |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
á |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
течет однородный ток 3 (рис. 4.5 в), поле |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в точке с радиусом ищется из теоремы |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j |
R |
о циркуляции: |
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
d |
|
|
|
|
â |
|
|
|
|
|
|
|
|
2 3 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
Рис. 4.5 |
|
|
|
|
|
Если же мы хотим определить вектор , |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
то, |
|
как можно понять |
из рис. 4.5 в, |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
это |
соотношение |
|
|
|
следует |
переписать |
|
в виде |
векторного |
произведения: |
|||||||||||||||||||||||||
, 2 Вычислим это поле в полости, имея в виду, что : |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
П |
1 |
|
|
|
|
|
|
|
|
1 |
, |
1 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||||||||||||||
Таким образом, поле в полости будет однородным и направлено в нашем случае снизу вверх.
2. По двум параллельным проводящим плоскостям текут антипараллельные токи с однородной линейной плотностью + C (рис. 4.6 а). Опреде-
лить величину и направление давления на каждую плоскость.
Решение. О направлении силы давления можно сказать сразу, что плоскости должны отталкиваться друг от друга. Вычислим поле, создаваемое токами
каждой плоскости (рис. 4.6 б). Ввиду |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
высокой |
симметрии задачи, |
силовые |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
линии должны быть просто прямыми, |
|
|
|
|
|
|
|
A |
|
|
|
B |
|
|
|
|
|
|||
параллельными плоскости. В каждом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
полупространстве поле однородно — |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
иначе мы могли бы построить кон- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
тур, который не пересекался бы током, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
но циркуляция поля по этому контуру |
|
|
i |
|
|
|
A |
|
|
|
|
B |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||
была бы ненулевой. На рисунке кон- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
тур — вид на левую пла- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
стину сверху — пронизывается током |
à |
|
|
|
|
|
á |
|
|
â |
|
|
|
|||||||
C , |
а циркуляция поля |
по нему |
|
|
|
|
|
|
|
|
Рис. 4.6 |
|
|
|
|
|
|
|||
равна 2 |
, так что поле в каж- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
дом полупространстве равно |
0 C2 |
В системе параллельных плоскостей |
||||||||||||||||||
(рис. 4.6 в) поле вне ее обратится в нуль, а между плоскостями будет равно
20, соответственно, индукция !0C. Но не все это поле надо подставлять
в закон Ампера, а лишь половину его, потому что ток каждой из плоскостей выталкивается полем другой плоскости, но сам себя он никуда толкать не
