8.4.1. Изохорный процесс

Процесс, протекающий при V=const, называется изохорным. Поскольку при изохорном процессе V=const, а dV=0, то dA=pdV=0, т.е. при изохорном процессе газ работу не совершает. Первое начало термодинамики запишется в этом случае в виде соотношения

dU = dQ.

Количество теплоты, которое необходимо сообщить системе для того, чтобы при постоянном объеме повысить его температуру на величину dT, можно выразить, если известна теплоемкость вещества при постоянном объеме dQ=C_VdT и, следовательно, dU=C_VdT. Принимая, что C_V - теплоемкость идеального газа не зависит от температуры, для внутренней энергии идеального одноатомного газа получим выражение

.

Для киломолей

.

Таким образом,

,

т.е. при изохорном изменении состояния газа вся подведенная к системе теплота идет на увеличение внутренней энергии системы.

8.4.2. Изотермический процесс

Процесс, происходящий при постоянной температуре, называется изотермическим процессом. При

T = const, U = const, dU = 0.

Уравнение первого начала термодинамики при изотермическом состоянии газа запишется в следующей форме:

dQ = dA. (8.3)

Из этого выражения следует, что при изотермическом процессе все подводимое к системе количество теплоты превращается в работу. Для подсчета работы, совершенной газом при изотермическом расширении от объема V₁ до V₂, необходимо проинтегрировать выражение для элементарной работы:

.

Выразив давление из уравнения Менделеева-Клайперона для одного моля газа

и подставив в уравнение для определения работы, получим

, .

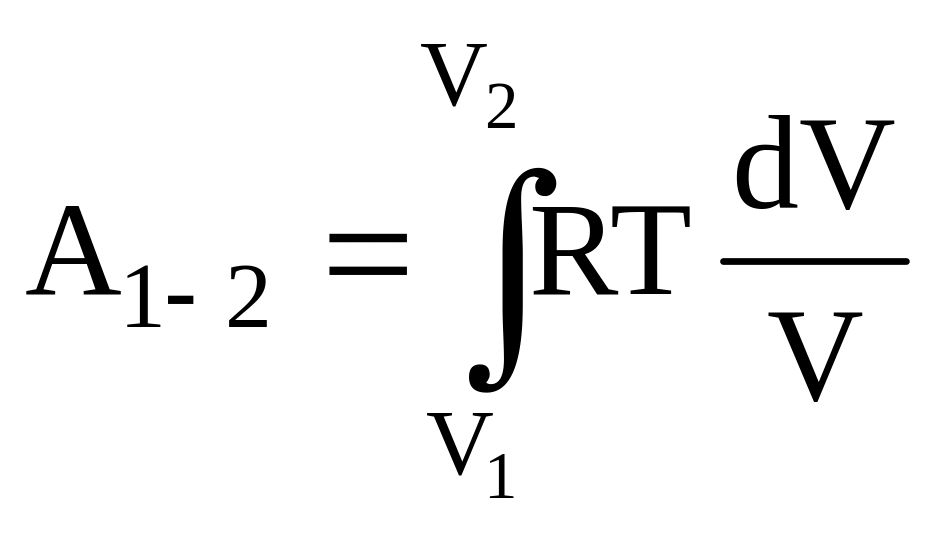Работа, совершаемая при расширении -молей газа, будет в раз больше, т.е.

.

Графически вычисленная работа (рис.8.6) выражается на диаграмме с координатами pV площадью аbcd, заштрихованной на графике. Вместо отношения , можно воспользоваться равным ему обратным отношением давлений, исходя из закона Бойля-Мариотта, тогда

. Согласно (8.3), при T=const Q=A, т.е. .

p a b d c V1 V2 V Рис.8.6

8.4.3. Изобарный процесс

Изобарный процесс – процесс, происходящий при постоянном давлении p=const. Работа в этом случае равна

.

Работа изображается на диаграмме (рис.8.7.) площадью прямо-угольника abcd.

Применим первое начало термодинамики к изобарному процессу dQ = dU + dA. Из определения молярной теплоемкости следует, что dQ = CpdT. Интегрируя выражение, по-лучим количество теплоты, необходимое для нагревания газа от температуры T1 до T2 для од-

р a b d c V1 V2 V Рис.8.7

ного моля газа

,

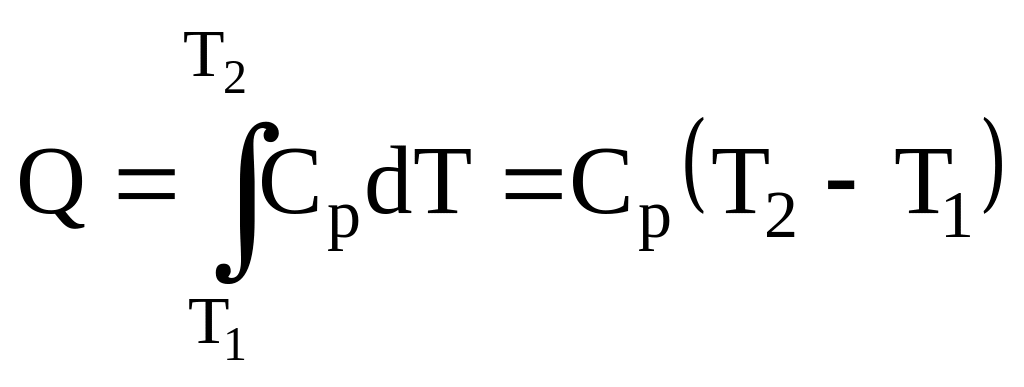для молей газа .

Таким образом, при изобарном процессе подводимое к газу тепло частично тратится на увеличение его внутренней энергии и частично на совершение работы.

При изобарном сжатии направление процесса меняется на обратное и работа, совершенная газом становится отрицательной dA0. Это означает, что не газ совершает внешнюю работу, а внешние силы совершают положительную работу dA по сжатию газа, т.е.

dA = dA.

Величина dU и dQ при этом также отрицательны, т.е. внутренняя энергия газа уменьшается за счет отдачи им тепла окружающим телам.