
- •Введение
- •Дифференцирование векторных величин
- •1. Кинематика поступательного
- •1.1. Система отсчета. Путь. Вектор перемещения
- •1.2. Скорость. Ускорение при криволинейном движении
- •1.3. Нормальное, тангенциальное и полное ускорения
- •1.4. Движение точки по окружности. Угловая скорость. Угловое ускорение
- •2. Динамика поступательного движения
- •2.1. Законы Ньютона
- •2.2. Силы в механике
- •2.2.1. Сила тяжести
- •2.2.2. Упругие силы
- •2.2.3. Сила трения
- •2.3. Внешние и внутренние силы. Закон сохранения импульса
- •3. Работа и энергия
- •3.1. Работа силы и ее выражение через криволинейный интеграл
- •3.2. Кинетическая энергия механической системы и её связь с работой
- •3.3. Потенциальная энергия материальной точки во внешнем силовом поле и ее связь с силой, действующей на материальную точку
- •3.4. Потенциальная энергия системы взаимодействия. Связь кинетической энергии системы с работой внутренних и внешних сил
- •3.5. Закон сохранения механической энергии. Закон сохранения и превращения энергии как проявление неуничтожимости материи и ее движения
- •3.6. Удар абсолютно упругих и неупругих тел
- •4. Динамика вращательного движения
- •4.1. Момент силы и момент импульса
- •4.2. Уравнение моментов
- •4.3. Движение центра тяжести твердого тела
- •4.4. Момент инерции тела относительно оси вращения
- •4.5. Уравнение динамики вращательного движения твердого тела относительно неподвижной оси. Закон сохранения момента импульса
- •4.6. Кинетическая энергия твердого тела. Работа внешних сил при вращении твердого тела
- •4.7. Кинетическая энергия при плоском движении твердого тела
- •5. Элементы специальной теории относительности
- •5.1. Преобразования Галилея. Механический принцип относительности
- •5.2. Постулаты специальной теории относительности. Преобразования Лоренца
- •5.3. Следствия из преобразований Лоренца
- •5.3.1. Одновременность событий в разных системах отсчета
- •5.3.2. Длина тел в разных системах отсчета
- •5.3.3. Длительность событий в разных системах отсчета
- •5.4. Пространственно-временной интервал
- •5.5. Релятивистская кинематика. Релятивистский закон сложения скоростей
- •5.6. Релятивистская динамика
- •6. Механические колебания и волны
- •6.1. Понятия о колебательных процессах. Гармонические колебания. Амплитуда. Частота. Фаза колебаний
- •6.2. Свободные гармонические колебания
- •6.2.1. Математический маятник
- •6.2.2. Пружинный маятник
- •6.2.3. Физический маятник
- •6.2.4. Скорость и ускорение точки, колеблющейся по гармоническому закону
- •6.2.5. Энергия гармонических колебаний
- •6.3. Сложение колебаний
- •6.3.1. Сложение колебаний одного направления и одинаковой частоты
- •6.3.2. Сложение двух гармонических колебаний одного направления, но разного периода
- •6.3.3. Сложение взаимно перпендикулярных колебаний
- •6.4. Затухающие колебания
- •6.5. Вынужденные колебания. Резонанс
- •6.6. Волновые процессы
- •6.6.1. Плоская синусоидальная волна. Фазовая скорость. Длина волны. Групповая скорость
- •6.6.2. Скорость распространения волн в упругой среде
- •6.6.3. Поток энергии в волновых процессах
- •6.6.4. Принцип Гюйгенса-Френеля. Интерференция волн
- •6.6.5. Отражение волн. Стоячие волны
- •7. Молекулярно-кинетическая теория
- •7.1. Статистический метод исследования. Термодинамический метод исследования. Термодинамические параметры. Равновесное состояние и процессы их изображения на термодинамических диаграммах
- •7.2. Основное уравнение молекулярно-кинетической теории газов
- •7.3. Средняя кинетическая энергия молекул. Молекулярно-кинетическое толкование абсолютной температуры. Связь основного уравнения мкт с уравнением Менделеева-Клайперона
- •7.4. Средняя скорость молекул. Поток молекул
- •7.5. Распределение молекул по скоростям. Закон Максвелла
- •7.6. Барометрическая формула.
- •7.7. Больцмановское распределение частиц в потенциальном поле. Закон Максвелла-Больцмана
- •7.8. Экспериментальный метод определения числа Авогадро
- •7.9. Эффективный диаметр молекулы. Число столкновений и средняя длина свободного пробега молекулы
- •7.10. Явления переноса в газах
- •7.10.1. Вязкость газов (внутреннее трение)
- •7.10.2. Закон Стокса
- •7.10.3. Теплопроводность газов
- •7.10.4. Диффузия газов
- •8. Термодинамика
- •8.1. Внутренняя энергия системы. Работа. Количество теплоты. Первое начало термодинамики
- •8.2. Степени свободы молекул. Распределение энергии по степеням свободы
- •8.3. Молекулярно-кинетическая теория теплоемкости газа
- •8.4.1. Изохорный процесс
- •8.4.2. Изотермический процесс
- •8.4.3. Изобарный процесс
- •8.5. Адиабатический процесс
- •8.7. Цикл Карно
- •8.8. Принцип действия тепловой и холодильной машин
- •8.9. Второе начало термодинамики
- •8.10. Приведенное количество тепла. Неравенство Клаузиуса
- •8.12. Статистический смысл второго начала термодинамики. Связь энтропии с термодинамической вероятностью
- •9. Агрегатные состояния и фазовый переход
- •9.1. Реальные газы. Уравнение Ван-дер-Ваальса
- •9.2. Экспериментальные изотермы. Критические состояния
- •9.3. Внутренняя энергия реального газа. Эффект
- •Библиографический список
- •Оглавление
7.4. Средняя скорость молекул. Поток молекул
Молекулы газа в каждый данный момент времени будут отличаться друг от друга не только своим местоположением в сосуде. Но и характером своего движения. Каждая молекула будет двигаться со своей скоростью i, отличающейся от скоростей других молекул по величине и направлению. Если объем, занимаемый газом, неподвижен, то все направления движения молекул равновероятны. Что же касается значений скоростей молекул по величине i, то различные скорости не равновероятны.
Энергия одноатомного идеального газа Е будет равна сумме кинетических энергий i всех его N молекул:
![]() .
.
Сталкиваясь друг с другом, молекулы непрерывно обмениваются энергией и, в принципе, возможно такое состояние газа, когда все его молекулы, за исключением одной, остановятся, а эта последняя будет двигаться с максимально возможной скоростью max, определяемой из соотношения
![]() .
.
Однако
такое неодновременное распределение
молекул по скоростям маловероятно. С
наибольшей вероятностью будут
осуществляться состояния, при которых
энергии различных молекул газа i
будут сравнительно близки друг к другу,
и мало отличаться от их среднего значения.
Средняя энергия поступательного движения
![]() молекул равна
молекул равна
![]() .
(7.9)
.
(7.9)
Величина
![]()
представляет собой средний квадрат скорости молекул газа. Извлекая из этой величины квадратный корень, мы получим величину, называемую средней квадратичной скоростью
![]() .
(7.10)
.
(7.10)
Средняя арифметическая скорость молекул газа определяется из соотношения
![]() .
(7.11)
.
(7.11)
Сопоставляя
(7.10) и (7.11), легко увидеть, что средняя
арифметическая величина скорости не
равна средней квадратичной и
![]() или
или
![]()
Расчет показывает, что
![]() ,
,
где m - масса одной молекулы.
Значение среднего квадрата скорости и средней квадратичной скорости можно определить, приравняв соотношения (7.7) и (7.9):
![]() .
.
Отсюда
![]() ,
а
,
а
![]() .
.
7.5. Распределение молекул по скоростям. Закон Максвелла
Предположим, что мы располагаем способом одновременного определения скоростей N-молекул некоторого количества газа. Изобразим полученные результаты в виде точек на оси . При этом мы получим «моментальную фотографию» скоростей молекул для некоторого момента времени t. Если бы все значения были одинаково вероятны, точки распределялись бы по оси равномерно (рис.7.3)
Рис.7.3 |
Однако скорости группируются в основном вблизи некоторого, наиболее вероятного значения. Близкие к нулю и очень большие значения скоростей встречаются сравнительно редко. Поэтому распределение точек по оси будет неравномерным с плотностью, различной на разных участках оси (рис.7.4).
Рис.7.4 |
Отношение числа точек N, попадающих в пределах интервала , к величине этого интервала, называется плотностью точек ():
![]() .
.
Если сопоставить ряд фотографий для разных моментов времени, то плотность будет различна. Для газа, находящегося в равновесном состоянии, т.е. для газа с неизменяющимися параметрами, плотность, с которой распределены точки на различных участках оси для всех моментов времени будет одна и та же.
Если взять несколько порций газа, находящегося в идентичных условиях, то распределение молекул по скоростям будет также идентично. Однако плотность точек по оси при одинаковом характере распределения по оси, очевидно, пропорциональна количеству молекул N и, следовательно, для различных порций газа будет различна. Одинаковым для различных порций будет соотношение
![]() .
(7.12)
.
(7.12)
Определенная таким образом функция f() характеризует распределение молекул газа по скоростям и называется функцией распределения, где
N = f() - число молекул, скорость которых больше , но меньше +;
![]() есть вероятность
того, что скорость молекулы будет иметь
значение в пределах данного интервала
скоростей.
есть вероятность
того, что скорость молекулы будет иметь
значение в пределах данного интервала
скоростей.
Попытаемся
найти аналитическое выражение закона
распределения молекулярных скоростей.
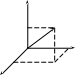
Скорость каждой молекулы изображается
вектором. В прямоугольной системе
координат вектор скорости
определяется координатами x,
y,
z
(рис.7.5). Очевидно, что эти координаты
одновременно будут являться компонентами
скорости вдоль выбранных осей координат.
Тогда число молекул
![]() ,
составляющие скорости которых больше
x,
но меньше x+x
согласно равенству (7.12), равны
,
составляющие скорости которых больше
x,
но меньше x+x
согласно равенству (7.12), равны
![]() .
(7.13)
.
(7.13)
Отношение
Рассуждая аналогично, можно написать выражение вероятности для молекул обладать составляющей скорости |
z
x x y y Рис.7.5
|
вдоль оси y, большей y и меньшей y+y:
![]() .
(7.14)
.
(7.14)
Вероятность составляющей скорости вдоль оси z, заключенной в пределах от z до z+z:
![]() .
(7.15)
.
(7.15)
Из
теории вероятности известно, что
вероятность совместного осуществления
трех независимых событий равна
произведению их вероятностей. Поэтому
вероятность
![]() для молекулы обладать скоростью,
компоненты которой заключены в пределах
от x,
y,
z,
до (x+x),
(y+y),
(z+z)
найдется перемножением 3-х вероятностей
(7.13), (7.14) и (7.15):
для молекулы обладать скоростью,
компоненты которой заключены в пределах
от x,
y,
z,
до (x+x),
(y+y),
(z+z)
найдется перемножением 3-х вероятностей
(7.13), (7.14) и (7.15):
![]() .
(7.16)
.
(7.16)
Допустим, что нижний предел скорости =const, в этом случае
![]() ;
;
xx+yy+zz = 0.
Допустим также, что
xyz = const.
При
выполнении этих предположений должна
оставаться неизменной и вероятность
![]() того, что молекула обладает скоростью,
удовлетворяющей сформулированным выше
требованиям. Если это так, то
того, что молекула обладает скоростью,
удовлетворяющей сформулированным выше
требованиям. Если это так, то
![]() ,
(7.17)
,
(7.17)
![]() .
(7.18)
.
(7.18)
Подставив в равенство (7.17) равенство (7.16) и учитывая (7.18), получим
![]()
Разделим полученное уравнение на произведение функций f(x)f(y)f(z), получим
![]() .
(7.19)
.
(7.19)
Умножим выражение (7.17) на произвольную величину , сложим с уравнением (7.19), сгруппируем члены в соответствии с индексами у и получим
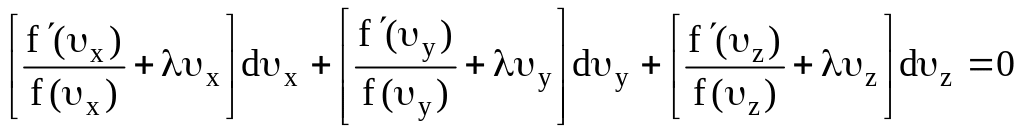 .
.
В силу произвольности величин dx, dy, dz написанное уравнение может выполняться в том случае, если каждый из стоящих в скобках двучленов порознь равен нулю, т.е.
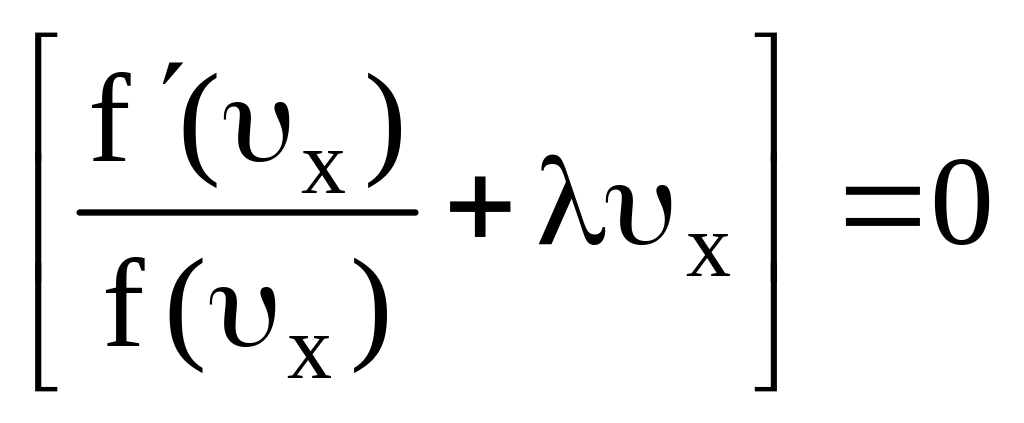 ;
(7.20)
;
(7.20)
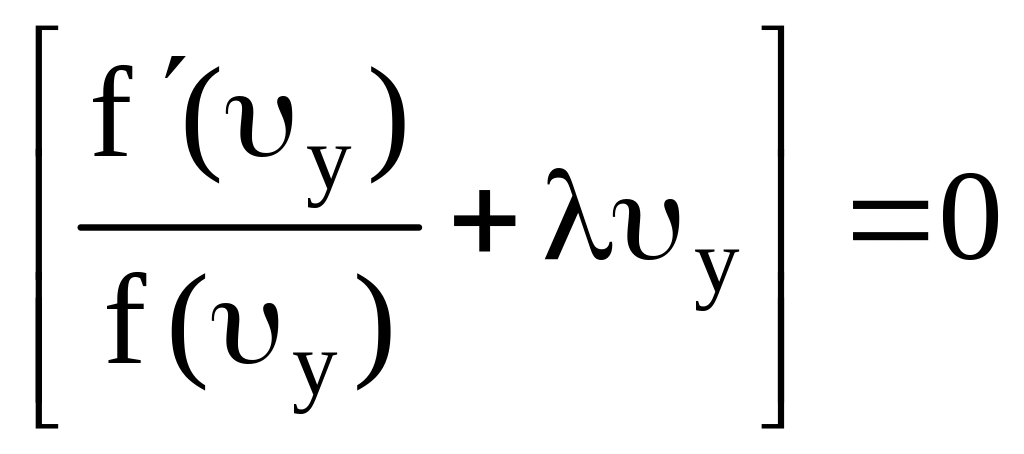 ;
(7.21)
;
(7.21)
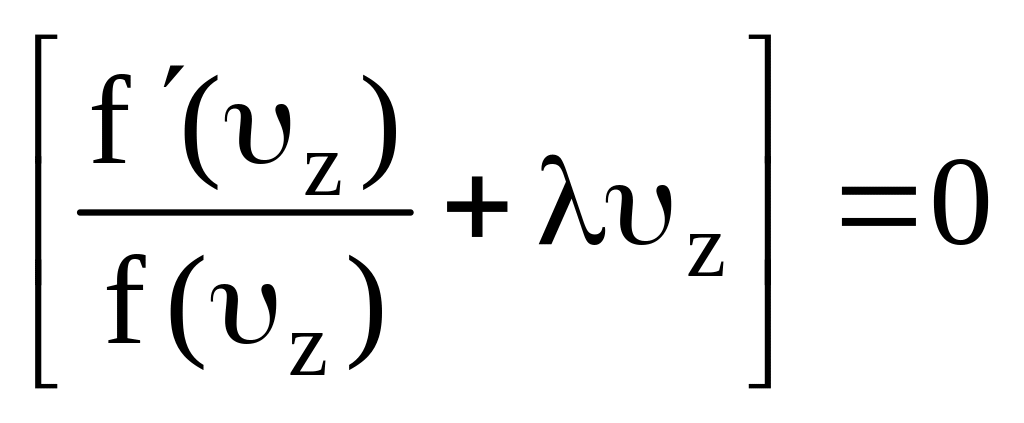 .
(7.22)
.
(7.22)
Обозначим
f(x,)=y,
тогда
![]() и (7.20) перепишется в виде
и (7.20) перепишется в виде
![]() .
.
После интегрирования
![]()
имеем
![]() ,
,
где А – постоянная интегрирования. Потенцируя данное выражение, получим
![]() .
.
Таким
образом, искомое выражение вероятности
![]() того, что скорость молекулы в направлении
оси x, заключенной в пределах от x
до x+x
будет равна
того, что скорость молекулы в направлении
оси x, заключенной в пределах от x
до x+x
будет равна
![]() .
.
Аналогичные выражения можно получить из (7.21) для вероятности того, что скорость молекулы вдоль оси y заключена в пределах от y до y+y и из (7.22) для вероятности того, что скорость молекулы в направлении оси z заключена в пределах от z до z+z.
Вероятность совместного события найдется перемножением соответствующих вероятностей, т.е.
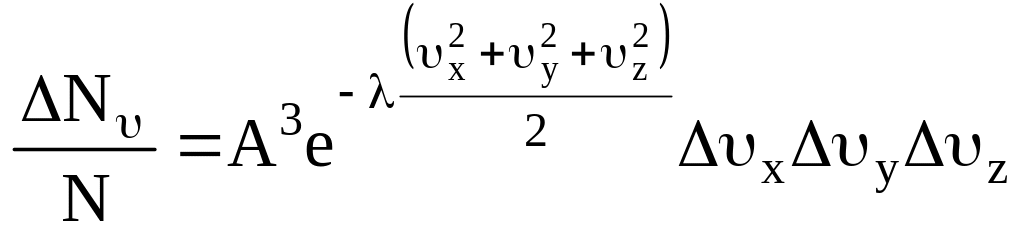 .
.
Если
в этом выражении заменить
![]() и определить значение постоянных, то
вероятность того, что молекула движется
независимо от направления со скоростью,
заключенной в пределах от
до +,
будет выражаться следующим соотношением
и определить значение постоянных, то
вероятность того, что молекула движется
независимо от направления со скоростью,
заключенной в пределах от
до +,
будет выражаться следующим соотношением
![]() ,
(7.23)
,
(7.23)
где m
- масса, k - постоянная
Больцмана, Т – абсолютная температура.
Учитывая, что
![]() ,
из (7.23) получим
,
из (7.23) получим
![]() .
(7.24)
.
(7.24)
Это выражение и является искомым законом распределения молекулярных скоростей Максвелла.
Таким образом, конкретный вид функции распределения зависит от рода газа (массы молекул) и от температуры. Давление газа и объем на распределение молекул по скоростям не влияют. Графическое изображение закона распределения Максвелла, представленном на рис.7.6.
+
вер
Рис.7.6
|
Из графика видно, что f() функция распределения стремится к нулю при 0 и . Следовательно, относительное число молекул в газе, обладающее очень малыми и очень большими скоростями ничтожно мало. Скорость, отвечающая макси-мальному значению функции распределения, будет, очевидно, наиболее вероятной.
|
Для
нахождения максимума функции f()
продифференцируем выражение (7.24), заменяя
через
![]() :
:
![]() ;
;
![]()
и, приравняв
к нулю
![]() ,
,
получим
![]() .
.
Значение , обращающее в нуль выражение, стоящее в скобках, представляет собой искомое вер:
![]() .
.
Вычисления показывают, что
,
![]() ,
,
поэтому
![]() .
.
При
возрастании температуры средняя скорость
![]() и наиболее вероятная скорость вер
увеличиваются пропорционально
и наиболее вероятная скорость вер
увеличиваются пропорционально
![]() ,
и максимум распределения сдвигается
вправо (рис.7.7). При этом число медленных
молекул убывает, а число быстрых –
возрастает. Но площадь под кривой, равная
полному числу всех молекул газа
,
и максимум распределения сдвигается
вправо (рис.7.7). При этом число медленных
молекул убывает, а число быстрых –
возрастает. Но площадь под кривой, равная
полному числу всех молекул газа
![]() ,
остается постоянной. Необходимо
подчеркнуть, что установленный Максвеллом
закон распределения молекул по скоростям
и все вытекающие из него следствия,
справедливы только для газа, находящегося
в равновесном состоянии.
,
остается постоянной. Необходимо
подчеркнуть, что установленный Максвеллом
закон распределения молекул по скоростям
и все вытекающие из него следствия,
справедливы только для газа, находящегося
в равновесном состоянии.
Закон справедлив для любого числа , если только это число достаточно велико.
Закон Максвелла – статистический закон, а законы статистики выполняются тем точнее, чем к большему числу одинаковых объектов они применяются. При малом числе объектов могут наблюдаться значительные отклонения от предсказаний статистики.
T2T1
T1 T2
0
Рис.7.7
|
Обратим внимание еще на следующие обстоятельства. При каждом столкновении молекул в газе изменяется не только направление, но и величины скоростей обеих сталкиваю-щихся молекул. Скорости одних молекул при этом увели-чиваются, других – умень-шаются. Но число молекул, ско- |
рость которых лежит в любом определенном интервале скоростей , не меняется.
Если в результате столкновений в единицу времени n молекул, обладавших скоростью в интервале , изменяют свою скорость, то ровно столько же молекул, обладавших ранее другими скоростями, приобретут в результате столкновений скорость в пределах .
Раз установившееся максвелловское распределение по скоростям в дальнейшем сохраняется. Более того, как показал Больцман, в результате взаимодействия между молекулами, каким бы ни было исходное распределение скоростей, в конце концов (весьма быстро) устанавливается максвелловское распределение.

 O
x x x x x x x x x x x
O
x x x x x x x x x x x
 O
x x x x x x x x x x x
O
x x x x x x x x x x x
 z
z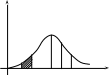 f()
f()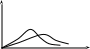 f()
f()