6.5. Вынужденные колебания. Резонанс

Для получения незатухающих колебаний необходимо воздействовать дополнительной переменной внешней силой, которая бы восполняла убыль энергии. Колебания системы, которые совершаются за счет работы периодически меняющейся внешней силы, называются вынужденными.

Пусть вынуждающая сила изменяется со временем по гармоническому закону

.

Тогда уравнение движения запишется следующим образом:

.

Разделим уравнение на m и введем обозначения

, , ,

получим неоднородное линейное дифференциальное уравнение второго порядка:

, (6.35)

где  - коэффициент затухания, - собственная частота колебаний системы.

Как известно из теории дифференциальных уравнений, общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. Общее решение однородного уравнения мы уже знаем, оно имеет следующий вид:

, (6.36)

,

где А₀ и  - произвольные постоянные.

Остается найти частное (не содержащее произвольных постоянных) решение уравнения. Будем искать это решение в виде

(6.37)

и попытаемся выяснить, не существует ли таких значений А и , при которых данная функция удовлетворяет уравнению (6.35).

Найдем производные

; (6.38)

. (6.39)

Подставим (6.37), (6.38) и (6.39) в уравнение (6.35):

.

Учтем, что

,

и перепишем предыдущее уравнение в следующем виде:

Сгруппируем члены при cost и sint:

(6.40)

Для того, чтобы уравнение (6.40) удовлетворялось при всех значениях t, необходимо, чтобы коэффициенты при sint и cost в левой и правой частях уравнения были одинаковы. Отсюда следуют два уравнения:

; (6.41)

. (6.42)

Возводя в квадрат и складывая их друг с другом, получим:

,

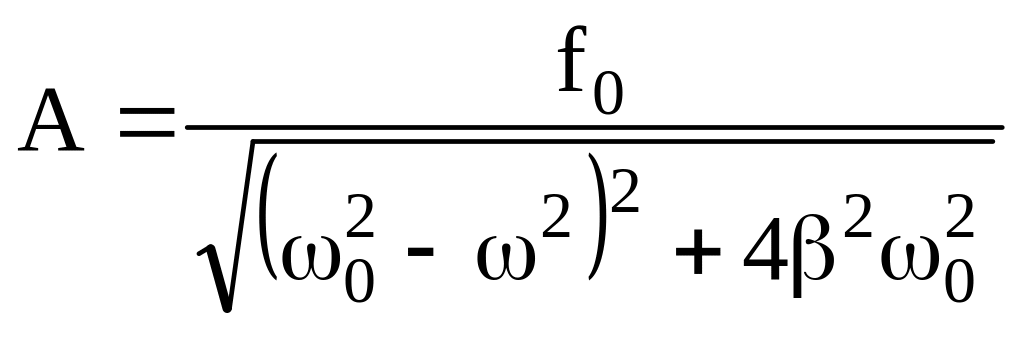. (6.43)

Из (6.43) следует, что амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы (f₀) и зависит от ее частоты ().

Из уравнения (6.42) найдем сдвиг фаз:

;

, (6.44)

т.е. вынужденные колебания сдвинуты по фазе относительно вынуждающей силы, причем величина сдвига фаз  зависит от частоты вынуждающей силы.

Подставляя (6.43) и (6.44) в уравнение (6.37), получим частное решение неоднородного уравнения:

. (6.45)

Функция (6.45) в сумме с (6.36) дает общее решение уравнения (6.35), которое описывает поведение системы при вынужденных колебаниях. Слагаемое (6.36) играет заметную роль только в начальной стадии процесса, с течением времени из-за экспоненциального множителя е^-t роль слагаемого (6.36) уменьшается и через некоторое время им можно пренебречь, сохраняя в решении слагаемое (6.45).

Таким образом, функция (6.45) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой, равной частоте вынуждающей силы.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (6.43) приводит к тому, что при некоторой, определенной для данной системы частоте, амплитуда колебаний достигает максимального значения.

Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а соответствующая частота – резонансной частотой. Чтобы определить резонансную частоту _рез, нужно найти максимум функции или минимум выражения, стоящего под корнем в знаменателе формулы (6.43). Продифференцируем это выражение по  и, приравняв нулю, получим:

. (6.46)

Уравнение (6.46) имеет три решения:

.

Решение, равное нулю, соответствует максимуму знаменателя. Отрицательное должно быть отброшено, так как оно лишено физического смысла (частота не может быть отрицательна). Таким образом, для резонансной частоты получается одно значение:

.

Подставив это значение частоты в (6.43), получим выражение для амплитуды при резонансе:

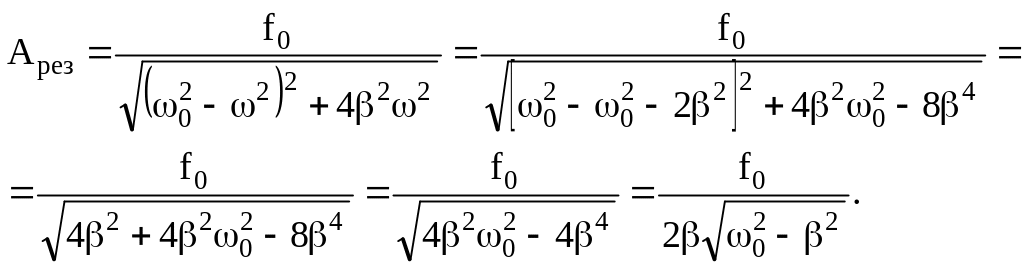
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы изображается графически (рис.6.17) и называется резонансной кривой.

A     рез  Рис.6.17

При 0 из уравнения (6.43) следует, что , т.е. при 0 все кривые приходят к одному и тому же предельному значению . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоян

ной величины f. Чем меньше , тем сильнее изменяется с частотой амплитуда, тем острее получается максимум. При стремлении  все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместиться из положения равновесия.