28 |
Sachin Bhalekar |
4.Numerical Simulations
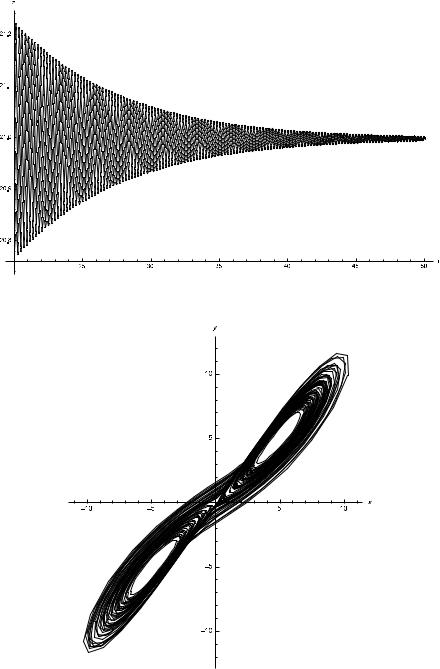
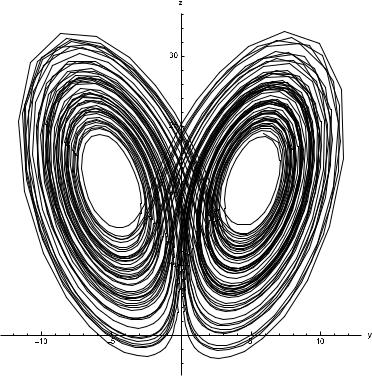
We consider the system(3.18) with a = 41, c = 31, e = 3.2 and b = 4. The equilibrium points are now E0 = (0, 0, 0) and E1,2 = (±5.123475, ±5.123475, 21). The saddle equilibrium E0 is useful in connecting chaotic scrolls and the scrolls will be around E1,2. The eigenvalues of Jacobian at E1,2 are −20.3789, 3.18947 ± 18.1059ı and the minimum effective dimension is turned out to be 0.888994. Numerical observations also show that the system is chaotic for α > 0.88. The stable orbits for α = 0.88 are shown in Figs. 1 whereas the chaotic attractors for α = 0.89 are shown in Figs. 2.
Figure 1a. Stable time series x(t) for α = 0.88. |
Figure 1b. Stable time series y(t) for α = 0.88. |
Complimentary Contributor Copy
Dynamics of Fractional Order Chaotic Systems |
29 |
Figure 1c. Stable time series z(t) for α = 0.88. |
Figure 2a. Chaotic xy-phase portrait for α = 0.89. |
5.Synchronization
Though the chaotic trajectories are aperiodic in nature, two different chaotic trajectories can oscillate together if the appropriate controller is applied [21, 22].
The chaos synchronization technique has been explored in secure communications [23]
Complimentary Contributor Copy
30 |
Sachin Bhalekar |
Figure 2b. Chaotic yz-phase portrait for α = 0.89. |
and cryptographic systems [24].
Deng and Li introduced the synchronization of fractional order chaotic systems in [25]. Since then various researchers presented different techniques of synchronization of chaos in fractional order systems. Now we utilize the nonlinear feedback control technique to synchronize the proposed fractional order chaotic system.
Consider the drive system as
Dαx |
= |
41(y − x), |
|
|
Dαy |
= |
−10x − xz + 31y, |
|
|
Dαz |
= |
3.2y2 − 4z |
(5.25) |
|
and response system as |
|
|
|
|
Dαx1 |
= |
41(y1 − x1), |
|
|
Dαy1 |
= |
−10x1 − x1z1 + 31y1 + u2, |
|
|
Dαz1 |
= |
3.2y12 − 4z1 + u3. |
(5.26) |
|
The nonlinear feedback controllers ui's are chosen as u2 = x1z1 − xz + 22y − 22y1 and u3 = 3.2(y2 − y12). If the errors in synchronization are termed as e1 = x − x1, e2 = y − y1 and e3 = z − z1 then the error system can be obtained by subtracting the system (5.26)
Complimentary Contributor Copy
Dynamics of Fractional Order Chaotic Systems |
31 |
Figure 3c. Chaotic xz-phase portrait for α = 0.89. |
from the system (5.25) as below |
|
|
|
Dαe1 |
= |
41(−e1 + e2), |
|
Dαe2 |
= −10e1 + 9e2, |
|
|
Dαe3 |
= |
−4e3. |
(5.27) |
The eigenvalues of the |
coefficient |
matrix |
of the error |
system |
(5.27) are |
−30.6629, −1.33712, −4. |
This shows |
that the |
errors will tend |
to zero |
as t tends to |
infinity. In the figs. 3 and 4 we show the synchronization of the system for fractional orders α = 0.80 and α = 0.98 respectively. The dashed lines in synchronized signals show the response signals whereas the solid lines show the drive signals. The solid lines, the dotted lines and the dot-dashed lines in Figs. 3(b) and 4(b) show the errors e1, e2 and e3 respectively.
6.Conclusion
In this chapter, we discussed the dynamics of fractional order chaotic system. It is observed that the nonlinear system with fractional system order less than three can exhibit
Complimentary Contributor Copy
32 |
Sachin Bhalekar |
Figure 3a. Synchronized signals x(t) and x1(t) for α = 0.80. |
Figure 3b. Errors in synchronization for α = 0.80.
chaos. Further, the synchronization of chaos is presented using nonlinear feedback control technique.
Complimentary Contributor Copy