0.5

x¯

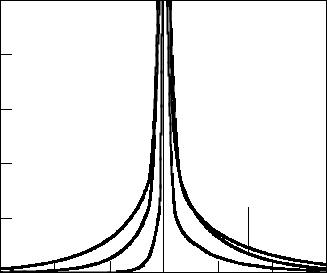
Figure 2. Dependence of the fundamental solution to the Cauchy problem on distance (the time-fractional advection-diffusion equation, α = 0.5).

4.Diffusive Stresses

The double Fourier transform applied to Eq. (43) gives:

The corresponding stress components are calculated according to (42) and have the

Complimentary Contributor Copy

Figure 3. Dependence of the stress component σxx on distance ((the classical advectiondiffusion equation, α = 1).

In the particular case of diffusive stresses caused by the solution to the standard advection-diffusion equation (α = 1) we obtain

To get the stress components (70)–(71) the polar coordinates in the (ξ, η)-plane have

Complimentary Contributor Copy

−0.15

x¯

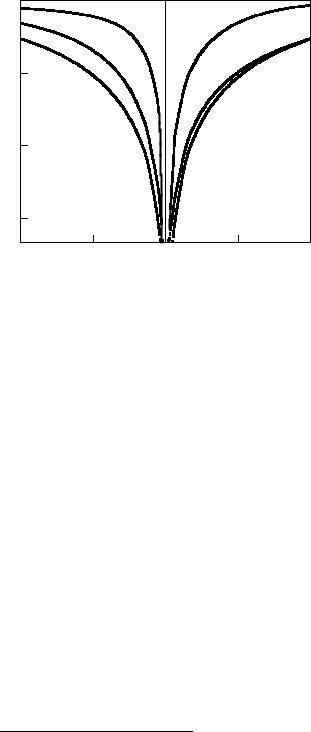
Figure 4. Dependence of the the stress component σxx on distance (the time-fractional advection-diffusion equation, α = 0.5).

and Prudnikov et al. (1983)

have been used. Additionally,

Another particular case α = 1/2 results in the stress component

Complimentary Contributor Copy

Dependence of the nondimensional quantity

atα

σ¯xx = 2µmp0 σxx

on the nondimensional coordinate x¯ for y¯ = 0 is shown in Fig. 3 for α = 1 and in Fig. 4 for α = 0.5.

5.Conclusion

We have analyzed the time-nonlocal generalizations of the constitutive equation for the matter flux resulting in fractional advection-diffusion equation. The theory of diffusive stresses associated with fractional advection-diffusion equation has been proposed. The fundamental solution to the Cauchy problem for such an equation has been considered in the case of two space variables, which has been solved using the integral transform technique. It should be emphasized that the fundamental solution to the Cauchy problem in the case 0 < α < 1 has the logarithmic singularity at the origin:

This result is similar to the case of the time-fractional diffusion equation when v = 0 (see Povstenko (2005) and Schneider (1990)). Such a singularity disappears only for the classical advection diffusion equation (α = 1). Due to singularity of the solution at the origin, in the case 0 < α < 1 drift caused by the quantity v is less noticeable than in the case α = 1 (compare Figs. 1 and 2 and Figs. 3 and 4).

References

Barkai, E., (2001). Fractional Fokker-Planck equation, solution, and application. Phys. Rev. 63, 046118.

Barkai, E., Metzler, R., Klafter, J., (2000). From continuous time random walks to the fractional Fokker-Planck equation. Phys. Rev. E 61, 132-138.

Bird, R.B., Stewart, W.E., Lightfoot, E.N., (2002). Transport Phenomena, 2nd ed. John Wiley & Sons, Inc., New York.

Cattaneo, C., (1948). On the conduction of heat. Atti Sem. Mat. Fis. Univ. Modena, 3, 83-101.

Chandrasekharaiah, D.S., (1986). Thermoelasticity with second sound: a review. Appl. Mech. Rev. 39, 355-376.

Chandrasekharaiah, D.S., (1998). Hiperbolic thermoelasticity: a review of recent literature.

Appl. Mech. Rev. 51, 705-729.

Compte, A., Metzler, R., (1997). The generalized Cattaneo equation for the description of anomalous transport processes. J. Phys. A: Math.Gen. 30, 7277-7289.

Datsko, B., Gafiychuk, V., (2012). Complex nonlinear dynamics in subdiffusive activatorinhibitor systems. Commun. Nonlinear Sci. Numer. Simulat. 17, 1673-1680.

Complimentary Contributor Copy

240 Yuriy Povstenko

Feller, W., (1971). An Introduction to Probability Theory and Its Applications, 2nd ed. John Wiley & Sons, New York.

Gafiychuk, V., Datsko, B., (2010). Mathematical modeling of different types of instabilities in time fractional reaction-diffusion systems. Comput. Math. Appl. 59, 1101-1107.

Green A.E., Naghdi, P.M., (1993), Thermoelasticity without energy dissipation. J. Elast. 31, 189-208.

Gurtin, M.E., Pipkin, A.C., (1968). A general theory of heat conduction with finite wave speeds. Arch. Rational Mech. Anal. 31, 113-126.

Huang, H., Cao, X., (2013). Numerical method for two dimensional fractional reaction subdiffusion equation. Eur. Phys. J. Special Topics 222, 1961-1973.

Huang, F., Liu, F., (2005). The time fractional diffusion equation and the advectiondispersion equation. ANZIAM J. 46, 317-330.

Ignaczak, J., Ostoja-Starzewski, M., (2010). Thermoelasticity with Finite Wave Speeds. Oxford University Press, Oxford.

Joseph, D.D., Preziosi, L., (1989). Heat waves. Rev. Modern Phys. 61, 41-73.

Jumarie, G., (1992). A Fokker-Planck equation of fractional order with respect to time. J. Math. Phys. 33, 3536-3542.

Karatay, I., Bayramoglu, S.R., (2012). An efficient scheme for time fractional advection dispersion equations. Appl. Math. Sci. 6, 4869-4878.

Kaviany, M., (1995). Principles of Heat Transfer in Porous Media, 2nd ed. Springer, New York.

Kilbas, A.A., Srivastava, H.M., Trujillo, J.J., (2006). Theory and Applications of Fractional Differential Equations. Elsevier, Amsterdam.

Liu, F., Anh, V., Turner, I., Zhuang, P., (2003). Time-fractional advection-dispersion equation. J. Appl. Math. Comput. 13, 233-245.

Lord, H.W., Shulman, Y., (1967). A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15, 299-309.

Metzler, R., Klafter, J., (2000). The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep. 339, 1-77.

Metzler, R., Klafter, J., (2004). The restaurant at the end of the random walk: recent developments in the description of anomalous transport by fractional dynamics. J. Phys. A: Math. Gen. 37, R161-R208.

Metzler, R., Barkai, E., Klafter, J., (1999). Anomalous diffusion and relaxation close to thermal equilibrium: a fractional Fokker-Planck equation approach. Phys. Rev. Lett. 82, 3563-3567.

Nield, D.A., Bejan, A., (2006). Convection in Porous Media, 3rd ed. Springer, New York. Nigmatullin, R.R. (1984a). To the theoretical explanation of the “universal response”. Phys.

Stat. Sol. (b) 123, 739-745.

Nigmatullin, R.R. (1984b). On the theory of relaxation for systems with “remnant” memory. Phys. Stat. Sol. (b) 124, 389-393.

Nowacki, W., (1974). Dynamical problems of thermodiffusion in solids. Bull. Acad. Polon. Sci., S´er. Sci. Techn. 23, 55-64, 129-135, 257-266.

Nowacki, W., Olesiak, Z.S., (1991). Thermodiffusion in Solids. Polish Scientific Publishers (PWN), Warsaw. (In Polish).

Parkus, H., (1959). Instationare¨ Warmenspannungen¨. Springer, Wien.

Complimentary Contributor Copy

Podlubny, I., (1999). Fractional Differential Equations. Academic Press, San Diego. Podstrigach, Ya.S., (1961). Differential equations of thermodiffusion problem in isotropic

deformable solid. Dop. Ukrainian Acad. Sci. 2, 169-172. (In Ukrainian).

Podstrigach, Ya.S., (1963). Differential equations of the diffusive strain theory of a solid. Dop. Ukrainian Acad. Sci. 3, 336-339. (In Ukrainian).

Podstrigach, Ya.S., (1965). Diffusion theory of inelasticity of metals. J. Appl. Mech. Techn. Phys. 2, 67-72. (In Russian).

Podstrigach, Ya.S., Povstenko, Y.Z., (1985). Introduction to Mechanics of Surface Phenomena in Deformable Elastic Solids. Naukova Dumka, Kiev. (In Russian).

Povstenko, Y., (2005). Fractional heat conduction equation and associated thermal stresses.

J. Thermal Stresses 28, 83-102.

Povstenko, Y., (2009a). Thermoelasticity which uses fractional heat conduction equation. J. Math. Sci. 162, 296-305.

Povstenko, Y., (2009b). Theory of thermoelasticity based on the space-time fractional heat conduction equation. Phys. Scr. T 136, 014017.

Povstenko, Y., (2011). Fractional Cattaneo-type equations and generalized thermoelasticity.

J. Thermal Stresses 34, 97-114.

Povstenko, Y., (2012). Theories of thermal stresses based on space-time-fractional telegraph equations. Comp. Math. Appl. 64, 3321-3328.

Povstenko, Y., (2013). Fractional thermoelasticity. In: Encyclopedia of Thermal Stresses, vol. 4. R.B. Hetnarski (ed.), Springer, Berlin, pp. 1778-1787.

Prudnikov, A.P., Brychkov, Yu.A., Marichev, O.I., (1981). Integrals and Series. Elementary Functions. Nauka, Moscow. (In Russian).

Prudnikov, A.P., Brychkov, Yu.A., Marichev, O.I., (1983). Integrals and Series. Special Functions. Nauka, Moscow. (In Russian).

Risken, H., (1989). The Fokker-Planck Equation. Springer, Berlin.

Scheidegger, A.E., (1974). The Physics of Flow Through Porous Media, 3rd ed. University of Toronto Press, Toronto.

Schneider, W.R., (1990). Fractional diffusion. In: R. Lima, L. Streit and R. Vilela Mendes (Eds.), Dynamics and Stochastic Processes, Lecture Notes in Physics, vol. 355, pp. 276–286. Springer, Berlin.

Sherief, H.H., El-Sayed, A.M.A., Abd El-Latief, A.M., (2010). Fractional order theory of thermoelasticity. Int. J. Solids Struct. 47, 269-275.

Van Kampen, N.G., (1981). Stochastic Processes in Physics and Chemistry. NorthHolland, Amsterdam.

Youssef, H.M., (2010). Theory of fractional order generalized thermoelasticity. J. Heat Transfer 132, 061301.

Zaslavsky, G.M., (2002). Chaos, fractional kinetics, and anomalous transport. Phys. Rep. 371, 461-580.

Zheng, G.H., Wei, T., (2010). Spectral regularization method for a Cauchy problem of the time fractional advection-dispersion equation. J. Comput. Appl. Math. 233, 2631-2640.

Complimentary Contributor Copy