
3268
.pdf
2.ИНТЕРФЕРЕНЦИЯ СВЕТА
4.71.Рассмотрим сложение двух гармонических
колебаний |
одного |
направления |
x1 |
acos 1t 1 |
и |
||||
x2 bcos 2t 2 . |
|
через , а частоту 2 представим |
|||||||
|
Обозначим частоту 1 |
||||||||
как |
2 . |
Тогда |
уравнения |
колебаний |
можно |
||||
переписать в виде |
x1 |
acos t , |
|
|
|
(1) |
|||
|
|
|
|
|
|
||||
|
|
|
x2 bcos t t , |
|
|
(2) |
|||
где |
t t 2 |
1 |
- разность |
фаз, |
зависящая |
от |
|||
времени. |
|
|
|
|
|
|
|
t |
|
|
По условию все значения разности фаз |
|
|||||||
равновероятны. Следовательно, разность фаз |
t за период |
||||||||
колебаний |
T или на промежутке |
значений |
0,2 , |
можно |
|||||
рассматривать как непрерывную, равномерно распределенную случайную величину с плотностью распределения f 1 2 . Математическое ожидание, т.е. среднее значение, случайной величины равно
2 . Математическое ожидание, т.е. среднее значение, случайной величины равно
2
M f d .
0
Функция cos случайного аргумента также является случайной величиной. Математической ожидание этой функции случайного аргумента равно
2 |
1 |
2 |
|
|
M cos cos f d |
cos d 0. |
|||
2 |
||||
0 |
0 |
|
||
|
|
|||
Отсюда делаем вывод: косинус разности фаз , значения |
||||
которой равновероятны, равен нулю, т.е. |
|
|
||
M cos cos |
0, |
(3) |
||
где - случайная переменная на промежутке |
0,2 . |
|||
81
Вернемся к вопросу сложения колебаний (1) и (2). Квадрат амплитуды результирующего колебания равен
A2 a2 b2 2abcos ,
где - случайная величина.
На основании свойства (3) A2=a2+b2. Поскольку энергия колебания пропорционально квадрату амплитуды, энергия результирующего колебания в данном случае равна сумме
энергий складываемых колебаний, т.е. |
|
|
|
|
|
||||||
|
|
|
|
W W1 W2 . |
|
|
|
(4) |
|||
Далее рассмотрим сложение взаимно перпендикулярных |
|||||||||||
колебаний x acos t , |
y bcos t . В этом случае точка |
||||||||||
состояния (x,y) на плоскости |
XY |
при |
|
0 |
и |
|
|||||
описывает эллипс, уравнение которого имеет вид |
|
|
|||||||||
|
x2 |
|
y2 |
|
2xy |
cos sin |
2 |
. |
|
(5) |
|
|
a2 |
b2 |
ab |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||
Как видно из уравнения (5), точка (x,y) совершает |
|||||||||||
колебания относительно начала |
0 при 0, , |
уравнения |
|||||||||
которых имеет вид |
|
x acos t , |
y bcos t . |
Квадрат |
|||||||
амплитуды колебаний в этих частных случаях A a2 |
b2 и, |
||||||||||
следовательно, полная энергия результирующего колебания будет равна сумме энергий слагаемых колебаний, т.е.
W W1 |
W2 . |
(6) |
Равенство (6) справедливо |
и в общем |
случае (5), |
поскольку с каждым движением и отклонением точки вдоль осей X и Y будет связана определенная часть полной энергии
Wconst.
4.72.Воспользовавшись моделью векторного сложения амплитуд гармонических колебаний одного направления, получим амплитуду результирующего колебания. Для этого перепишем уравнения заданных колебаний через одну тригонометрическуюфункцию:
82

|
acos t , |
|
|
|
|
|
|
|
|
|
|
10 |
|||
|
2 |
2acos |
t |
|
|
, |
|||||||||
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
3 |
1,5acos t |
|
|
|
. |
|
|
|
|
|||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
Векторная диаграмма приведена на |
|
||||||||||||||
рисунке. |
Измерение |
|
|
|
|
модуля |
|
||||||||
результирующей амплитуды |
|
|
|
|
|
|
|
|
|||||||
|
0 |
|
10 |
20 30 |
дает |
0 |
1,9a |
|
|||||||
4.73. Имеет место сложение гармонических колебаний одного направления k acos t k 1 , где k=1,2,…, N.
Надо найти амплитуду результирующего колебания.
Решение этой задачи методом построения векторных диаграмм дано в сборнике задач (см. ответы и решения). Наряду с этим, предложим аналитический способ решения этой задачи. При этом воспользуемся показательной формой представления колебания. Ка-тое колебание запишем в виде
k |
|
a |
ei t k 1 e i t k 1 . |
(1) |
|
||||
|
2 |
|
|
|
Поскольку показательные функции, находящиеся |
в |
|||
скобках комплексно сопряженные, уравнение (1) запишем в виде
|
k |
aRe ei t k 1 , |
|
|
(2) |
|
где символ Re выделяет реальную часть выражения (1). |
|
|
||||
Уравнение результирующего колебания получает вид |
||||||
N |
N |
|
|
N |
|
. (3) |
R aRe ei t k 1 |
aRe ei t ei k 1 |
|
||||
1 |
1 |
|
|
1 |
|
|
|
N |
|
|
|
|
|
Выражение |
ei k 1 |
представляет собой сумму членов |
||||
|
1 |
|
|
|
|
|
конечной геометрической прогрессии, первый член которой a1=1 и знаменатель q ei . Следовательно,
83

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
q |
N |
1 |
|
|
|
|
|
iN |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei k 1 |
|
|
|
|
e |
. |
|
|
|
|
|
|
|
|
|
|
|
(4) |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
q 1 |
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Преобразуем правую часть (4): |
|
|
|
|
|
N |
|
|
|
|
|
|
|
N |
|
|
|
N |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
eiN 1 |
|
|
|
|
cosN isin N 1 |
|
|
|
sin |
|
|
|
|
|
|
|
icos |
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
ei 1 |
|
|
|
cos isin 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
icos |
|
|
|
|
sin |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
2 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
sin |
N |
|
|
|
|
N |
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
icos |
|
|
|
|
icos |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
sin |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
sin |
N |
|
|
|
N 1 |
|
|
|
N 1 |
|
|
|
|
|
sin |
|
N |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
i N 1 2 |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
isin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Таким образом, получаем: |
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ei k 1 sin |
|
|
e i N 1 |
|
|
|
sin |
. |
|
|
|
|
|
(5) |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||
С учетом (5) получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
asin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N 1 |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
2 |
|
|
Re e |
i t N 1 2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(6) |
||||||||||||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos t |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
sin |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Отсюда амплитуда результирующего колебания |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A asin |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
(7) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Решение (6) полезно еще и тем, что оно определяет и фазу колеблющейся величины .
84

4.74. Согласно заданным |
|
|
|
|
|||
условиям, |
|
дипольные |
|
|
|
k2 |
|
излучатели 1 и 2 расположены в |
|
|
r1 |
M k1 |
|||
плоскости, |
проходящей |
через |
|
|
E2 |
||
центры |
диполей |
и |
|
1 |
r |
r2 |
|
перпендикулярной |
|
их |
d |
O |
E1 |
||
электрическим |
моментам. |
|
|
||||
|
|
|
|
||||
Отсюда |
следует, |
что |
|
2 |
|
|
|
электрические векторы E1 |
и E2 |
|
|
|
r |
||
|
|
|
|
||||
электромагнитных |
|
полей |
|
|
|
|
|
осциллирующих диполей колеблются в этой плоскости и |
|||||||
перпендикулярно радиус-векторам r1 |
и r2 , проведенным от |
||||||
центров диполей к точке наблюдения M (см. рисунок). |
|||||||
Разумеется, что речь идет о какой-либо точке M волновой |
|||||||
зоны. С учетом разности фаз α между колебаниями |
|||||||
излучателей напишем уравнение для электрической |
|||||||
напряженности в точке M электромагнитных полей: |
|||||||
|
|
|
|
E |
|
|
a0 |
|
cos t kr , |
(1) |
|||||||
|
|
|
|
|
r |
|
|||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|||||
|
|
|
|
|
|
|
1 |
|
|
|
|
||||||
|
|
E |
|
|
|
|
a0 |
|
cos t kr |
. |
(2) |
||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
2 |
|
|
|
|
|
r |
2 |
|
|||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
Здесь предполагается, что мощности излучателей равны |
|||||||||||||||||
между собой, а также |
|
k1 |
|
|
|
k2 |
|
k 2 . Разность фаз между |
|||||||||
|
|
|
|
||||||||||||||
колебаниями (1) и (2) в точке M равна |
|
|
|||||||||||||||
|
|
|
|
|
|
|
k r2 r1 . |
(3) |
|||||||||
Из |
рисунка |
|
видно, |
|
что |
r1 r d 2 cos |
и |
||||||||||
r2 r d |
2 cos (до малых величин второго порядка). Тогда |
||||||||||||||||
разность фаз |
|
|
|
|
|
|
|
|
kd cos . |
(4) |
|||||||
|
|
|
|
|
|
|
|
|
|
||||||||
Заметим, что когерентности колебаний в точке M |
|||||||||||||||||
необходимо, чтобы угол между волновыми векторами k1 |
и k2 |
||||||||||||||||
был малым, что равносильно условию d <<r1, r2 . |
|
||||||||||||||||
85

Квадрат амплитуды результирующего колебания равен
A2 A2 |
A2 |
2A A cos , |
(5) |
|
1 |
2 |
1 |
2 |
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
A |
a0 |
|
,A |
a0 |
. |
|
(6) |
||||
|
|
|
|
|
|
r |
|
|
|||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
r |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
Подставляя (4) и (6) в (5), получим |
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
||||
A2 |
a0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
r2 |
1 (d /2r)cos |
|
1 (d /2r)cos |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos kdcos . |
(7) |
||||
|
2r cos |
|
|
d 2r cos |
|||||||||||||||
1 d |
|
1 |
|
|
|
|
|||||||||||||
При условии d<<r выражение (7) получает вид |
|
||||||||||||||||||
|
|
|
|
|
A2 |
|
2a2 |
1 cos kdcos . |
|
(8) |
|||||||||
|
|
|
|
|
|
0 |
|
|
|||||||||||
|
|
|
|
|
r2 |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Поскольку |
интенсивность |
|
излучения пропорциональна |
||||||||||||||||
квадрату амплитуды колебаний электрической напряженности, максимальная интенсивность будет наблюдаться в тех
направлениях, для |
которых |
cos kdcos 1, |
т.е. |
когда |
|||||||
kd cos 2 n, где n = 0, 1, 2, ,или |
|
|
|
||||||||
|
|
2 n |
|
|
|
|
|
|
9 |
||
cos |
|
|
|
|
n |
|
d. |
|
|||
|
kd |
|
|
|
|||||||
|
|
|
|
|
|
|
2 |
|
|
||
Далее, ответим на вопрос пункта б). При cos , т.е. |
|||||||||||
когда cos 1, выражение (8) принимает вид |
|
|
|||||||||
|
A2 |
2a2 |
1 cos kd . |
|
10 |
||||||
|
0 |
|
|||||||||
|
r2 |
|
|||||||||
|
|
|
|
|
|
|
|
A Amin |
0 |
|
|
Из равенства |
(10) |
видно, |
что |
при |
|||||||
cos kd 1, т.е когда разность фаз между колебаниями
d |
1 |
|
|
A Amax |
cos kd 1, |
||
излучателей 2 |
|
|
|
|
. В случае |
||
|
|
||||||
a |
2 |
|
|
|
|
||
или 2 d .
.
86

4.75. В предыдущей задаче 4.74 было получено выражение (8) для квадрата амплитуды электромагнитного излучения в экваториальной плоскости двух дипольных
осцилляторов. Зависимость интенсивности излучения |
I |
|||||||||||||||||||
подобна зависимости |
A2 . |
Если в этой формуле, |
согласно |
|||||||||||||||||
условию |
задачи, положить |
d 2, то |
зависимость |
I |
||||||||||||||||
примет вид |
I0 1 cos cos . |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
I |
|
(1) |
|||||||||
|
|
Для построения диаграммы направленности излучения |
||||||||||||||||||
диполей зависимость (1) удобнее представить в виде |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
I I0 2cos2 cos 2 . |
|
(2) |
||||||||||
|
|
На основании уравнения (2) построим диаграммы |
||||||||||||||||||
направленности излучения при следующих ограничениях: |
|
|||||||||||||||||||
|
|
|
|
а) |
|
0. При этом условии |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
2cos |
|
|
|
cos . |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приведем координаты некоторых точек полярной кривой |
||||||||||||||||||
для |
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
θ |
|
0 |
|
/6 |
|
/4 |
|
/3 |
/2 |
|||||||||||
ρ |
|
0 |
|
0,08 |
|
|
0,4 |
|
|
1 |
|
2 |
||||||||
Примерный вид кривой (диаграммы) показан на рисунке.
б) . В этом случае
|
2 |
|
|
|
||
2cos |
|
|
|
cos |
|
. |
|
2 |
2 |
||||
|
|
|
|
|
||
z
Кривая будет представлять ту же кривую, повернутую на 900 либо по часовой стрелке, либо против. Осуществив оборот полярной кривой вокруг оси Z , получим поверхность, характеризующую распределение интенсивности излучения в пространстве.
87

4.76.Обратимся к формуле (2) задачи 4.75. Подставляя
вэту формулу соотношение d , получим зависимость
|
2cos2 cos 2 . |
(1) |
Для 0 |
и на основании (1) получим уравнения |
|
полярных диаграмм направленности излучения: |
|
|
|
2cos2 cos , |
(2) |
|
2sin2 cos . |
(3) |
4.77. В этом случае в формулу (2) задачи 4.75 подставляем d 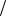 4 и
4 и  2. При этом получаем зависимость
2. При этом получаем зависимость
|
2 |
|
|
2 |
|
|||
2cos |
|
|
|
cos |
|
|
|
. |
|
2 |
|
2 |
|||||
|
|
|
|
|
|
|||
4.78. На оси Z (см. рисунок) расположена система параллельных и равноотстоящих вибраторов. Плоскость рисунка совмещена с экваториальной плоскостью вибраторов. Круг радиуса R является кругом обзора. В экваториальной
плоскости |
излучающего диполя напряженность Ei Ei |
Eir 0 не |
зависит от азимутального угла . Амплитуда |
|
напряженности |
z |
|
|
|
(n ) |
|
M |
|
(n 1) |
|
r1 |
|
r r |
|||
|
|
||
d O |
2 |
||
|
x |
||
n |
|
||
R |
|||
(n 1) |
|
результирующего поля E Ei
в произвольной точке М волновой зоны будет определяться регулярностью расположения вибраторов, их предварительной разностью фаз, а также дополнительной разностью фаз, приобретаемой лучами прохождением разных путей до точки М.
88

Разность фаз между колебаниями световых векторов в точке М, обусловленными приходящими волнами от источников n и n 1 равна
|
2 |
r |
r |
2 |
d sin . |
|
|
||||
|
2 |
1 |
|
||
В точке М будет наблюдаться максимум излучения, если выполняется условие 2 k , где k 0, 1, 2,.... Тогда
2 d sin 2 k .
Отсюда получаем
|
d |
|
|
2 k |
|
sin . |
|
|
|||
|
|
При непрерывном изменении угла обзора с угловой скоростью угол t. Следовательно,
|
d |
|
|
2 k |
|
sin t . |
|
|
|||
|
|
Заметим, что если в точке М выполняется условие кратности 2 k для волн, приходящих от соседних диполей n и n 1 , то это условие также выполняется для волн от других дипольных пар, симметрично расположенных относительно точки O.
4.79. Полагаясь на рисунок, находим разность фаз между соседними колебаниями световых векторов в точке М, обусловленных приходящими волнами от действительного S и мнимого S источников:
k(r |
r ) |
2 |
2hsin . |
|
|||
2 |
1 |
|
|
|
|
|
|
|
|
|
x |
|
|
|
r1 |
x |
////////////////////////////// |
M |
|
|
|
|||
S |
|
|
|
|
|
|
r2 |
|
|
|
|
|
|
O |
|
|
|
|
|
З |
|
|
|
S' |
|
|
89

Когерентность колебаний в точке М имеет место, когда угол наблюдения полосы на экране и расстояние h будут малыми величинами. В этом случае
sin tg x ,
где x- координата точки М (см. рисунок), и разность фаз
4 hx .
.
Для светлых интерференционных полос
4 hx 2 k, |
(1) |
для темных 2k 1 , где k 0,1,2,....
Под шириной x интерференционной полосы будем понимать расстояние между левым и правым соседними минимумами, что равнозначно расстоянию между двумя соседними светлыми или темными полосами. Из условия (1) имеем:
x xk xk 1 2h. |
2 |
||
Увеличивая h на Δh, получим |
|
По |
|
x |
2 h h . |
||
условию задачи x x , т.е. 1 h h , или |
|
||
h 1 h. |
|
(3) |
|
Из равенства (2) имеем |
|
|
|
h 2 x . |
|
(4) |
|
Подставляем (4) в(3): h 1 |
|
. Отсюда получаем |
|
|
|||
2 x
длину волны
2 h x
1 .
Для заданных значений h, x, и l длина волны
0,6 мкм.
4.80.Ситуация, предложенная условиями задачи, показана на рисунке. Из рисунка видно, что разность фаз между колебаниями световых векторов в точке М
90
