
2906
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 / 2 |
2 / 2 |
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 uˆ . |
(1.22) |
|
|
|
2 / 2 |
2 / 2 |
||||||||||||
|
|
|
|||||||||||||
|
|
|
0 |
|
|
1 |
|
|
|
0,5a |
|
||||
где uˆ |
1, |
T |
- базовые перемещения. |
|
|||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правильность этих соотношений легко проверяется с по- |
|||||||||||||||
мощью соотношений кинематики. |
|
|
|||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 / 2 |
2 / 2 |
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
. |
|||||
|
|
D |
2 / 2 |
2 / 2 |
0 |
||||||||||
|
|
|
0 |
1 |
0,5a |
|
|||||||||
Система уравнений равновесия (1.21) может быть решена без использования деформационных соотношений, поскольку рассматриваемая стержневая система статически определима. Ниже приводится решение, которое применимо и к статически
неопределимым системам. |
|
|
|
|
|
|
|
|
|
|
||||||
|
Система (1.22) запишется в виде |
|
D |
1 , |
2 , |
T . |
||||||||||
|
При одинаковых E и F , жесткости стержней будут равны |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
c1 |
c2 |
EF /( |
2a ), |
c3 |
EF / a . |
Матрица нормальных сил |
||||||||||
|
|
|
( EF / a )D |
1 , |
2 , |
T , |
где |
J диагональная матри- |
||||||||
N |
C |
|
||||||||||||||
|
j11 |
|
|
j 22 |
|
|
|
|
j 33 |
|
||||||
ца с элементами |
1 / |
2 , |
1 / |
2 , |
1. Тогда сис- |
|||||||||||
тема уравнений равновесия примет вид |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
M T . |
||
|
|
|
RN |
( EF / a )RJD |
1 , |
2 , |
0, 0, |
|||||||||
В результате преобразований получается система
|
|
|
|
|
|
2 / 2 |
2 / 2 |
0 |
|||
|
|
|
|
|
|
2 / 2 |
2 / 2 |
0 |
|||
0 |
1 |
0,5a |
|||
1
2
1
2M 1 . EF
1
Отсюда определяются базовые перемещения 1 0 ,
2  2
2
 2M /( EF ),
2M /( EF ),  4( 1
4( 1 
 2 )M /( EFa ) . Нормальные си-
2 )M /( EFa ) . Нормальные си-
135
|
|
|
|
|
лы в стержнях будут равны N1 |
2M / a , N2 2M / a , |
|||
N 3  2M / a .
2M / a .
§ 8. МБП для пространственных стержневых систем Пространственные стержневые системы, предназначенные
для крепления твердых тел друг к другу, широко применяются в технике и строительстве. Ниже предлагается метод расчета нормальных сил и перемещений в пространственных статиче-
ски определимых и неопределимых стержневых шарнирных или близких к ним системах. Эти системы могут включать и твердые недеформированные тела. Рассматривается матричная форма описания основных соотношений метода, как наиболее удобная для пространственных систем и систем, имеющих большое количество
базовых перемещений.
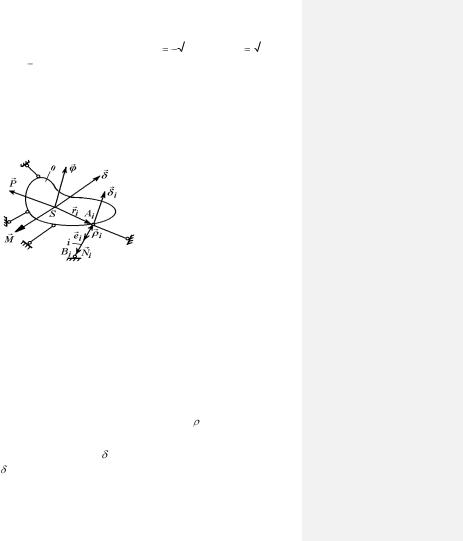
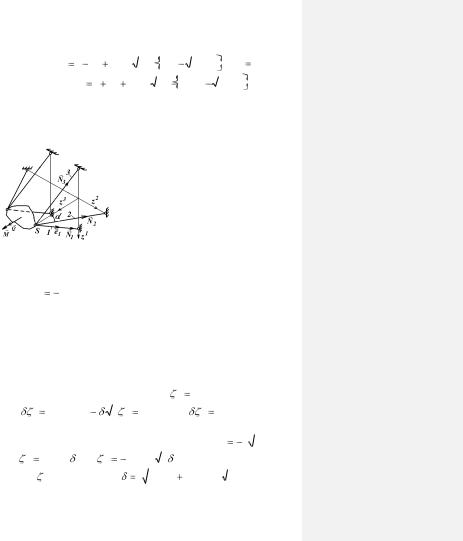
Рассматривается система с одним твердым телом, изобра-
женная на рис. 1.14, где 0- диск; i=1, 2, …, n- номер стержня;
P, M - главные вектор и момент системы внешних сил, при-
ложенных к телу, приведенные к точке S; Ai , Bi - подвижный и неподвижный узлы, соединяющие стержень i с телом и
опорным телом; ei - орт оси стержня, направленный из центра подвижного узла в центр неподвижного узла; N i - нормальная сила в стержне i (на рисунке нормальные силы условно показаны как реакции, приложенные к телу); i - вектор-радиус
узла Ai относительно узла Bi ; r i - вектор-радиус узла Ai от-
носительно точки S ; - поступательное перемещение тела;i - полное перемещение узла Ai .
Для рассматриваемой системы базовыми перемещениями
136

удобно считать вектор поступательного перемещения тела и угол поворота тела , который при малом модуле может так-
же считаться вектором . Подобные базовые перемещения позволяют в соответствии с теоремой теоретической механики
о представлении перемещений твердого тела определить пере- |
||||
мещение любой точки тела на основе соотношения |
|
|
||
|
|
|
i |
|
|
|
|||
|
ri , где |
r i - вектор - радиус этой точки. |
|
|
|
Предполагается, что количество и расположение стержней |
|||
таково, что кинематическая изменяемость системы исключена. |
||||||
|
|
|
|
|
|
|
Пусть |
i |
|
i , где |
|
, |
i - линейные перемещения узла |
Ai за счет действия силы |
|
|
||||
P |
|
и момента M соответственно |
||||
(вектор i |
перпендикулярен оси вращения тела). При малых |
|||||
углах поворота , характерных для деформируемых систем,
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
ri |
и полное перемещение узла Ai i |
|
|
ri . |
|||||
|
Удлинение стержня i , вызванные перемещением точки |
||||||||||
Ai , |
li |
|
|
|
|
|
|
|
|
|
|
|
i |
ei , а нормальная сила в стержне i |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ni |
|
Ni ei |
ci li ei |
ci (( |
|
ri ) |
ei ) |
ei , |
(1.23) |
|
где ci |
Ei Fi |
/ li - жесткость стержня; li , |
Fi , |
Ei - длина, пло- |
|||||||
щадь поперечного сечения и модуль упругости материала стержня.
Уравнения равновесия твердого тела
n
i 1 n
i 1
|
Ni |
|
ei |
P, |
|
|
|
|
M S ( Ni )
|
|
(1.24) |
n |
|
|
( ri |
ei )Ni |
M . |
i 1 |
|
|
|
Пусть rim ( m |
1, 2, 3 ) - проекция вектор – радиуса ri на |
||||||
ось |
zm |
системы координат, а |
rˆ |
r1 |
, r 2 |
, r 3 T |
- матрица – |
|
|
i |
|
|
i |
i |
i |
i |
|
столбец размерности 3, где «Т» - символ операции транспони- |
|
|
ˆ |
рования. Аналогично вводятся матрицы eˆ i , ˆ , M , |
P . Тогда |
137 |
|

|
|
|
|
|
|
|
|
|
|
|
|
|
векторное произведение gi |
( ri |
|
ei ) можно записать в виде |
|||||||||
gˆ i D( rˆi )eˆ i , где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
r 3 |
r 2 |
|
|
|
|
|
|
D( rˆ ) |
|
r 3 |
|
|
0 |
r1 . |
|
|
|
|
|
|
|
|
r 2 |
|
r1 |
0 |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
Пусть N |
N1, N2, ..., N n |
- матрица нормальных сил, |
||||||||||
|
g 1 |
g 1 |
... |
g |
1 |
|
|
e1 |
e1 |
... |
e1 |
|
|
1 |
2 |
|
|
n |
|
|
1 |
2 |
|
n |
|
G |
g 2 |
g 2 |
... |
g |
2 |
, |
H |
e2 |
e2 |
... |
e2 |
- |
|
1 |
2 |
|
|
n |
|
|
1 |
2 |
|
n |
|
|
g 3 |
g 3 |
... |
g |
3 |
|
|
e3 |
e3 |
... |
e3 |
|
|
1 |
2 |
|
|
n |
|
|
1 |
2 |
|
n |
|
матрицы размерности 3 |
n . Тогда уравнения равновесия при- |
|||||||||||
мут вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
ˆ |
0 . |
|
(1.25) |
|||
|
|
GN |
|
|
HN |
|
||||||
|
|
M , |
P |
|
||||||||
Выражение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
A |
0,5( |
( ri |
ei )Ni |
ei |
Ni |
) |
|
|
|||
|
|
i 1 |
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
ˆ ) |
|
|
|
||
|
|
0,5(( GN )T |
ˆ |
( HN )T |
|
|
|
|||||
определяет работу упругого деформирования стержней систе-
мы. Здесь знак ―-― обусловлен тем, что сила N i считается при-
ложенной к твердому телу и направленной к точке закрепле-
ния стержня на опоре и тем, что на перемещении точки креп-
ления стержня к телу при удлинении стержня сила N i совер-
шает отрицательную работу. Очевидно, что
|
|
|
|
|
|
|
|
где |
A |
0,5( N T GT ˆ |
N T H T ˆ ) |
0,5N T |
|
, |
|
1, |
2, ..., n T |
- матрица абсолютных удлинений |
|||||
стержней.
Следовательно, для определения абсолютных удлинений стержней, нет необходимости строить картину перемещений точек и тел системы. Для этого нужно транспонировать матрицы G и H , которые получаются при составлении уравне-
138

ний равновесия системы, и использовать выражение
|
GT ˆ H T ˆ . |
(1.26) |
|
Следует отметить, что это верно только при соответствии системы уравнений равновесия системе базовых перемещений: если каждому уравнению равновесия в проекциях на некоторую ось системы координат соответствует линейное базовое перемещение вдоль этой оси, а уравнению равновесия моментов, приложенных к телу, относительно некоторой точки, соответствует угловое базовое перемещение этого тела относительно этой же точки.
Пусть |
|
|
c1 |
|
|
T |
- матрица - столбец жесткостей |
||||||
c |
|
, c2 ,..., cn |
|||||||||||
стержней, |
I - единичная матрица размерности n |
n . Тогда |
|||||||||||
матрица жесткостей стержней C |
|
|
. По определению нор- |
||||||||||
I c |
|||||||||||||
мальной силы |
|
|
|
. Поэтому система уравнений равнове- |
|||||||||
N |
C |
|
|||||||||||
сия примет вид |
|
|
|
|
|
|
|
|
|
|
|||
GC( G |
T |
ˆ |
H |
T ˆ |
) |
ˆ |
HC( G |
T |
ˆ |
H |
T ˆ |
|
ˆ |
|
|
M , |
|
|
) P . (1.27) |
||||||||
При одном твердом теле разрешающая система уравнений задачи содержит всего шесть уравнений независимо от количества стержней, соединяющих тело с опорой. Это следует из того, что число базовых перемещений, определяющих перемещение любой точки тела, равно количеству независимых уравнений равновесия тела. Поэтому исчезает различие в методах решения задач для статически определимых и неопределимых систем.
Особенно удобен МБП при решении задач с большим числом неизвестных, например для маховиков со спицами или многостержневых статически неопределимых систем.
§ 9. Примеры решения МБП задач для пространственных стержневых систем в матричной форме
Пример 14. Определение нормальных сил и перемещений в пространственной трехстержневой системе
139

Пусть три одинаковых стержня имеют длину l , площадь S , изготовлены из материала с модулем упругости E и обра-
зуют ферму, изображенную на рис. 1.15, где |
|
|
/ 6 . Тогда |
|||||||||||||||||
ci EF / l |
c . Пусть проекции силы P определены матрицей- |
|||||||||||||||||||
столбцом |
ˆ |
P |
1 |
,0,P |
3 |
T |
, а |
моментная |
нагрузка |
отсутствует. |
||||||||||
P |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проекции ортов ei |
на оси системы координат есть компоненты |
|||||||||||||||||||
матриц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eˆ1,3 |
|
|
|
|
T , |
eˆ2 0;0,5; |
|
|
T , |
|
||||||||||
|
0,5;0; |
|
3 / 2 |
|
3 / 2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0,25 |
0 |
3 / 4 |
|||||||
|
|
|
|
|
|
|
|
|
|
B1,3 |
0 |
|
0 |
|
|
0 |
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
3 / 4 |
0 |
|
|
0,75 |
|||||
|
0 |
0 |
|
0 |
|
||
|
|
|
|
|
|
|
|
B2 |
0 |
0,25 |
3 / 4 . |
||||
|
|
|
|
|
|
||
|
0 |
|
3 / 4 |
0,75 |
|||
|
|
|
|
Поскольку |
|
0 , |
для описания |
|||||||||||
Рис. 1.15 |
|
|
равновесия фермы достаточно сис- |
|||||||||||||||
|
|
темы уравнений равновесия сил |
|
|||||||||||||||
|
|
|
|
|
||||||||||||||
|
4 |
|
ˆ |
|
4 |
ˆ |
|
|
ˆ |
|
|
ˆ |
|
|
|
|||
|
c Bi |
c |
Bi |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
c Bp |
|
P , |
|
|
||||||||
|
i 1 |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5 |
|
0 |
|
|
|
|
|
0 |
|
|
|
|
||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bp |
Bi |
|
0 |
0,25 |
|
|
|
3 / 4 . |
|
|
|||||||
|
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
3 / 4 |
|
2,25 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
Проекции орта перемещения точки S на оси системы ко- |
||||||||||||||||||
ординат |
1 2P1 /( c |
), |
|
2 |
2P3 |
|
|
|
) , |
3 |
2P3 |
/( 3c ) . |
||||||
|
/( 3c |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
i )2 |
|
|
|
Из условия нормировки модуля орта |
|
( |
1 |
опре- |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
||
|
|
|
|
|
|
|
||||||||||||
деляется |
величина |
|
|
36( P1 )2 16( P3 )2 |
/ 3c . Проекции |
нор- |
||||||||||||
мальных сил в стержнях на оси координат определяются мат-
140
рицами
ˆ |
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
T |
|
ˆ |
|
0 . |
|
( |
P |
P |
/ |
3 ) 0,5;0; |
3 / 2 |
|
|
|||||||||||||||
|
|
|
|
|||||||||||||||||||
N1 |
|
|
|
|
, N2 |
|
||||||||||||||||
|
ˆ |
|
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
( |
P |
|
P |
/ 3 ) |
0,5;0; |
3 / 2 . |
|
||||||||||||||
|
N1,3 |
|
|
|
|
|
||||||||||||||||
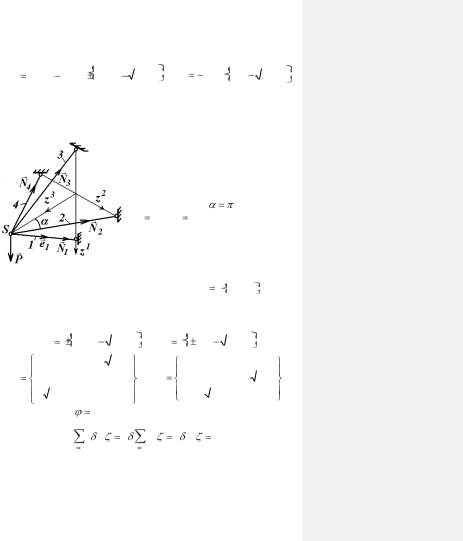
Пример 15. Определение нормальных сил и перемещений в пространственной стержневой ферме
Пусть две симметрично расположенные фермы поддерживают твердое тело, нагруженное силой Q и моментом М, приложенными в плоскости симметрии и направленными вдоль оси z3 (рис. 1.16). Из условий закрепления тела следует, что перемещение точки S в направлении оси
Рис. 1.16 z2 будет равно нулю. Из условий равновесия тела следует, что проек-
|
|
ция на ось z1 силы P , приложенной в узле S к ферме, будет |
|
равна P1 |
M / a , где a - расстояние между точками крепле- |
ния тела. |
Неизвестные проекции P2 и P3 этой силы должны |
быть такими, чтобы проекция перемещения точки S на ось z2
была равна нулю. Проекции ортов ei на оси системы координат и матрицы Bi и Bp остаются прежними, поскольку отра-
жают свойства деформируемой системы, а не нагрузки. Поэтому изменится только правая часть системы уравнений рав-
новесия, которая с учетом того, что |
2 |
0 принимает вид |
||||||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
1 |
2P1 / c , |
3 3 4P2 / c , 9 3 |
4P3 / c . |
|||||||||||
Из второго и третьего уравнений получается соотношение |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
между неизвестными проекциями |
P2 |
|
и P3 |
P3 |
|
3 3P2 , то- |
||||||||
гда 1 |
2P1 /( c ) , 3 |
|
4P2 |
|
|
|
|
|
||||||
|
/( |
3 c ) . Из условия нормиров- |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ки орта |
определяется |
2 |
|
3( P1 )2 |
|
4( P2 )2 |
/( |
3c ) . Проекции |
||||||
|
|
141 |
|
|
|
|
|
|
|
|
|
|||
нормальных сил в стержнях на оси координат определяются матрицами
ˆ |
( P |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
T |
ˆ |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
T |
|
|
2P |
) |
0,5;0; |
3 / 2 , |
|
2P |
0;0,5; |
|
|
3 / 2 . |
|||||||||||||||||||||||
N1,3 |
|
|
|
|
N2 |
|
|
|
|
||||||||||||||||||||||||
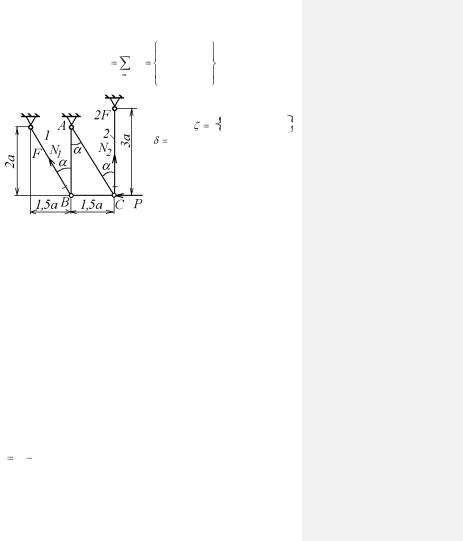
Пример 16. Определение нормальных сил и перемещений |
|
||||||||||||||||||||||||||||||||
|
в пространственной четырехстержневой ферме |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть |
четыре |
одинаковых |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
стержня имеют длину l , площадь |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S , изготовлены из материала с |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
модулем упругости E и образуют |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
осесимметричную ферму (рис. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1.17), |
|
где |
|
|
|
|
/ 6 . |
|
|
|
|
Тогда |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ci |
EF / l c . Пусть сила P име- |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ет |
произвольное |
|
направление в |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
плоскости перпендикулярной оси |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
и ее проекции на оси системы |
||||||||||||||||||
|
Рис. 1.17 |
|
|
|
|
координат определены матрицей |
|||||||||||||||||||||||||||
|
|
|
|
- |
столбцом |
|
ˆ |
|
P ,P 0 |
T |
, а мо- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
ментная нагрузка отсутствует. Проекции ортов ei |
на оси сис- |
||||||||||||||||||||||||||||||||
темы координат есть компоненты матриц |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
eˆ1,3 |
|
|
|
|
|
T , |
eˆ2,4 |
|
|
|
|
|
|
T , |
|
|
|
|
||||||||||||||
|
|
0,5;0; |
|
3 / 2 |
0; |
0,5; |
|
|
3 / 2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
0 |
|
|
|
||||
|
0,25 |
|
|
|
0 |
|
3 / 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
B1,3 |
|
0 |
|
|
|
|
0 |
|
|
0 |
|
, |
B2,4 |
0 |
|
0,25 |
|
3 / 4 . |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
3 / 4 |
|
|
0 |
|
0,75 |
|
|
|
|
|
|
0 |
|
3 / 4 |
0,75 |
|
||||||||||||||||
|
Поскольку |
|
|
|
0 , для описания равновесия фермы доста- |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
ˆ |
|
|
4 |
|
|
ˆ |
|
ˆ |
|
ˆ |
|
|
|
|
|
|
|
|
|
|
||||
точно системы |
|
|
|
c Bi |
|
c |
|
|
|
Bi |
c Bp |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
P , где |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
i |
|
1 |
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
142 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
4 |
0,5 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bp |
|
Bi |
0 |
0,5 |
0 . |
|
|
|
|
|
i |
|
1 |
0 |
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Решение |
этой |
системы |
|||||
|
|
имеет |
|
|
|
|
|
вид |
||
|
|
|
|
ˆ |
|
1 |
|
2 |
|
T |
|
|
|
|
P |
/ P; P |
/ P;0 , |
||||
|
|
|
|
|
|
|
||||
|
|
|
2P / c . |
Следовательно, |
на- |
|||||
|
|
правление |
перемещения |
узла |
||||||
|
|
S |
совпадает с направлением |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
силы |
P . |
|
|
|
|
|
|
|
|
|
|
Столь же простым оказы- |
|||||||
|
|
вается и решение о воздейст- |
||||||||
|
|
вии |
произвольно направлен- |
|||||||
ной силы P на неосесимметричную ферму.
§ 10. Исследование статически неопределимых стержневых систем с использованием уравнений совместности перемещений
В данном параграфе рассматривается традиционный подход к рассмотрению статически неопределимых систем, основанный на использовании уравнений совместности перемещений (деформаций). Этот параграф можно изучать независимо от изложенного выше материала.
Пусть для некоторой системы можно составить n независимых уравнений статики. Пусть нормальные силы в стержнях системы определяются m неизвестными величинами. Стержневая система будет статически определимой, если число неизвестных m не превышает число независимых уравнений n равновесия, составленных по правилам статики. Если число неизвестных больше возможного числа уравнений равновесия, система становится статически неопределимой. Величина
l m n называется степенью статической неопределимости системы. Для рассмотрения статически неопределимых стержневых систем необходимо, в дополнение к уравнениям
143
ки, составить уравнения совместности перемещений. Число уравнений совместности перемещений должно соответствовать числу "лишних" неизвестных системы (термин «лишних» надо понимать как «нормальных сил в стержнях, не требующихся для обеспечения равновесия системы»).
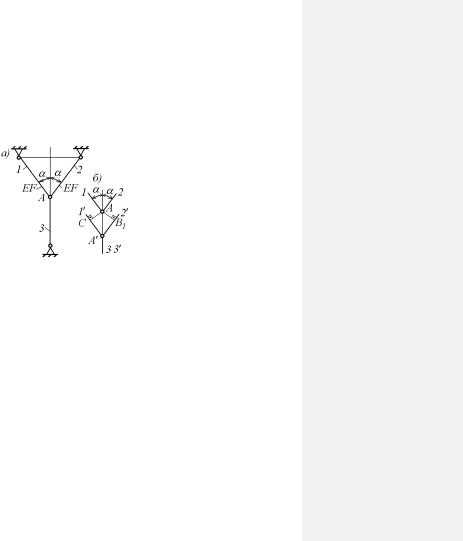
Например, в системе, изображенной на рис 1.19, один из стержней является лишним и без него равновесие тела АВС может быть обеспечено.
Число лишних неизвестных определяет степень статической неопределимости стержневой системы. Если система имеет одну, две и т.д. лишних неизвестных, то ее называют один раз (или однажды), два раза (или
дважды) и т.д. статически неопределимой. Число уравнений совместности перемещений должно соответствовать степени
статической неопределимости.
Наиболее трудной частью изучения статически неопределимых систем является составление уравнений перемещений, которые отражают большое разнообразие физических явлений, происходящих в системе. Необходимо отметить, что если в статически определимых системах силы в их упругих элементах могут возникать только от активных и реактивных внешних сил, то в статически неопределимых системах эти силы могут возникать и по другим причинам, например, от изменения температуры, а также от неточностей изготовления элементов системы.
Уравнения совместности перемещений отражает очевидный факт: концы стержней деформированной системы должны оставатъся в тех же шарнирах, что и недеформированной, даже если эти шарниры перемещаются. Например, в системе, изображенной на рис. 1.18, шарниры В и С будут поворачиваться вокруг шарнира А, так как соединяют стержни 1 и 2 с жестким
144
