
2906
.pdf
Итак, момент силы относительно точки О равен нулю, когда |
|
||||||
сила равна нулю или когда линия ее действия проходит через |
|
||||||
данную точку. Из рис. 1 видно, что |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|M0 ( P )| =2 пл. |
OAB, |
(2) |
|
|||
т. е. величина (модуль) момента силы относительно данной |
|
||||||
точки численно равна удвоенной площади треугольника, осно- |
|
||||||
ванием которого является сила, а вершиной - данная точка. |
|
||||||
Для плоской системы сил момент силы относительно точ- |
Отформатировано |
||||||
ки определяется его проекцией на ось перпендикулярную этой |
|
||||||
плоскости, направленную к наблюдателю. Эту проекцию так- |
|
||||||
же называют моментом силы. Для плоской системы сил мо- |
|
||||||
мент силы относительно точки равен взятому со знаком плюс |
|
||||||
или минус произведению силы на ее плечо. Момент считается |
|
||||||
положительным, если он способен вызвать вращение против |
|
||||||
хода часовой стрелки. Момент противоположного направле- |
|
||||||
ния считается отрицательным. |
|
|
|
||||
Вектор момента силы относительно точки. |
|
||||||
|
|
При решении задач статики и динами- |
|
||||
|
ки удобно считать момент силы относи- |
|
|||||
|
тельно точки вектором. |
|
|
||||
|
|
Векторомрадиусом точки А прило- |
|
||||
|
жения силы P относительно точки О на- |
|
|||||
|
зывают вектор r , проведенный из точки О |
|
|||||
Рис. 2 |
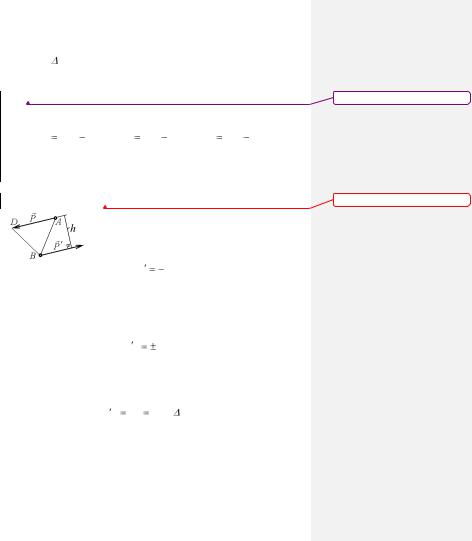
в точку А (рис. 2). |
|
|
||||
|
Вектором моментом силы |
|
|||||
|
|
P относи- |
|
||||
тельно точки О (центр момента) называют вектор, равный век- |
|
||||||
торному произведению вектора - радиуса точки приложения |
|
||||||
силы на вектор силы |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Mo ( P ) r P |
(3) |
|
|||
Очевидно что, модуль вектора момента силы относительно |
|
||||||
данной точки численно равен удвоенной площади треугольни- |
|
||||||
ка, основанием которого является сила, а вершиной данная |
|
||||||
точка (рис. 2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
| M o ( P )| |
|
2пл |
OAB . |
(4) |
|
|
|
|
|
|
140 |
|
|
|
|
|
|
|
|
|
|
|
Если вектор силы P переносить по ее линии действия, то площадь OAB не будет меняться, и, следовательно, если силу переносить по ее линии действия, то вектор момент силы относительно данной точки будет неизменным.
Проекции вектора - момента силы относительно точки О на оси координат, проходящие через точку О, определяются соотношениями
Mox |
Pz y Py z , Moy Px z Pz x , Moz Py x Px y , |
|
|
|
|
|
|
где x, y, z |
- координаты точки приложения силы |
P ; Px , |
Py , |
Pz - проекции силы P на оси координат.
Момент пары сил
Парой сил (или просто парой) в механике называется особая система сил, состоящая из двух равных по модулю, противоположно направленных параллельных сил
|
|
|
|
|
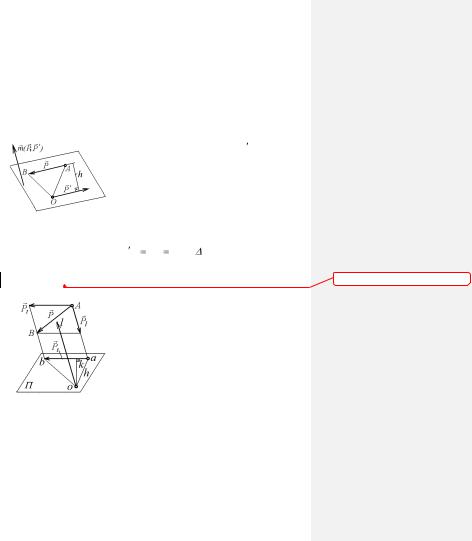
Рис. 3 |
(рис. 3): |
P |
P . Расстояние h между ли- |
|
ниями действия сил пары называют плечом |
||||
|
||||
пары.
Модулем момента пары сил называют алгебраическую величину, равную произведению модуля одной из сил пары на ее плечо
|
|
m( P,P ) Ph . |
(5) |
Если плечо h заменить твердым стержнем, то при его вращении под действием сил пары против хода часовой стрелки в формуле (5) надо ставить знак плюс, а при вращении по ходу
часовой стрелки - знак минус. Согласно рис. 5 имеем |
|
|
|
| m( P,P )| Ph 2 пл ABD |
(6) |
т. е. модуль момента пары численно равно удвоенной площади треугольника, основанием которого является одна из сил пары, а вершина находится в любой точке на линии действия второй силы пары.
Свободным вектором называют вектор, который можно,
141
Отформатировано
Отформатировано
не меняя его величины и направления, переносить параллельно самому себе.
В сопротивлении материалов вектор силы или момента можно считать свободным только при описании равновесия тела (гипотеза отвердевания). При определении внутренних сил в теле силы и моменты уже нельзя считать свободными векторами, поскольку от положения силы или момента относительно тела зависят напряжения и деформации тела.
Моментом пары m( P,P ) называют
свободный вектор, равный по модулю произведению модуля одной из сил пары на ее плечо (рис.4) и направленный перпендикулярно плоскости пары в ту сторону, чтобы, смотря из его конца к
Рис. 4 началу, видеть вращение пары против хода часовой стрелки
|
|
| m( P,P ) | Ph 2 пл. OAB . |
(7) |
Момент силы относительно оси |
Отформатировано |
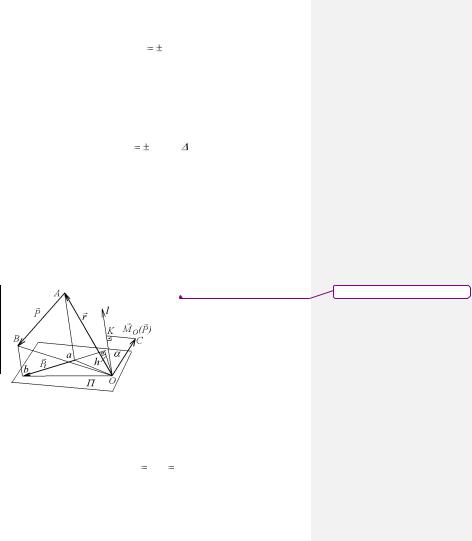
Вращательное действие силы относительно оси определя-
ется не всей силой, а только ее состав-
ляющей (компонентой) Pt (рис. 5), ле-
жащей в плоскости, перпендикулярной
этой оси. Другая составляющая Pl , па-
раллельная оси l, не вызывает вращения, а стремится сдвинуть тело вдоль оси (силой такого направления дверь
снимают с петель).
Моментом силы относительно оси называют алгебраическую величину, равную произведению проекции силы на плоскость П, перпендикулярную к данной оси, на расстояние от этой проекции до оси, равное длине перпендикуляра, опущенного из точки пересечения оси с плоскостью на линию действия проекции (рис. 5):
142
|
Pt h . |
|
(8) |
|
|
Ml ( P ) |
|
|
|||
Момент считается положительным, если, смотря в направ- |
|
||||
лении, противоположном направлению оси, можно видеть |
|
||||
|
|
|
|
|
|
вращение тела вокруг оси под действием силы P |
(или состав- |
|
|||
|
|
|
|
|
|
ляющей Pt ) против хода часовой стрелки. При вращении по |
|
||||
ходу часовой стрелки момент считается отрицательным. Из |
|
||||
формулы (8) и рис. 5 следует |
|
|
|
|
|
|
|
Oab , |
|
(9) |
|
Ml ( P ) |
2 пл |
|
|
||
|
|
|
|
|
|
т. е. момент силы P относительно оси l численно равен взятой |
|
||||
с соответствующим знаком величине удвоенной площади тре- |
|
||||
|
|
|
|
|
|
угольника, основанием которого служит проекция силы P на |
|
||||
плоскость, перпендикулярную к оси, а вершиной - точка пере- |
|
||||
сечения оси с плоскостью. Если сила параллельна оси, то Pt = |
|
||||
0, а если ее линия действия пересекает ось, то h = 0. В обоих |
|
||||
|
|
|
|
|
|
случаях согласно (8) Mt ( P ) = 0, т. е. момент силы относи- |
|
||||
тельно оси равен нулю, когда сила параллельна оси или ее пе- |
|
||||
ресекает. В обоих случаях сила и ось расположены в одной |
|
||||
плоскости. |
|
|
|
|
|
|
|
В тех случаях, когда сила |
Отформатировано |
||
|
не известна, а известен только |
|
|||
|
момент силы, для оценки |
|
|||
|
вращательного действия мо- |
|
|||
|
мента силы вокруг оси ис- |
|
|||
|
пользуется проекция момента |
|
|||
|
силы на эту ось. |
|
|
||
|
|
Момент силы относи- |
|
||
|
тельно оси l равен проекции |
|
|||
Рис. 6 |
ОК на эту ось вектора момен- |
|
|||
|
|
|
|
|
|
|
та силы MO( P ) (рис. 6), взя- |
|
|||
того относительно произвольной точки на данной оси и обо- |
|
||||
|
|
|
|
|
|
значается символом Ml ( P ). |
|
|
|
|
|
|
|
|
|
||
Ml ( P ) |
OK |
npl Mo( P ) |
(10) |
|
|
Момент силы относительно оси не зависит от выбора точ-
143
ки О оси, из которой проводится вектор– радиус r в точку А
приложения силы P .
Сумма векторов моментов двух сил, составляющих пару, относительно произвольной точки О не зависит от положения точки О и равна вектору моменту пары, то есть вектору моменту одной из сил пары относительно точки приложений второй силы пары.
В частном случае на плоскости сумма моментов двух сил, составляющих пару, относительно произвольной точки в плоскости пары равна моменту пары
|
|
|
|
M ( P ) + M ( P ) = m( P,P ) . |
(11) |
||
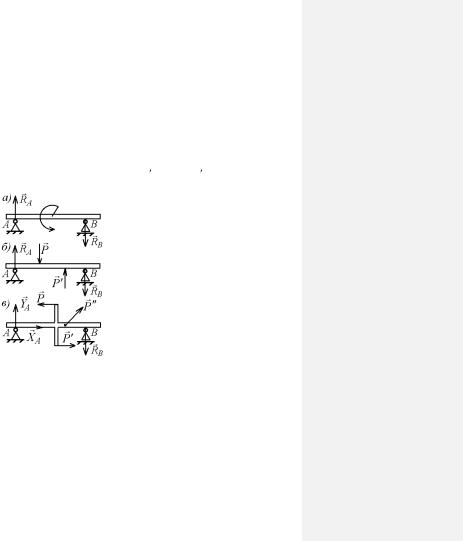
Часто пару изображают в виде изогнутой стрелки с обозначением момента (рис. 7, а). Такое упрощенное изображение оправдано тем, что действие пары сил характеризуется ее моментом, и при определении опорных реакций, т. е. неизвестных внешних сил следует брать суммы моментов всех сил относительно какой - либо точки, а где приложены силы, составляющие пару, на основании (7) значения не имеет. Но, если надо определить не внешние силы, а внутренние в разных сечениях балки, как
Рис. 7 это делается в сопротивлении материалов, то важно знать, где приложе-
ны силы пары. Например, внутренние силы будут различными для балок, изображенных на рис. 7, б и 7, в. Если силы пары приложены, как показано на рис. 7, в, то пара и ее момент условно называют сосредоточенными.
Наиболее распространенными опорами тел являются шарнирно подвижная опора, шарнирно неподвижная опора и заделка.
Шарнирно подвижная опора (рис. 7,а, б, опора В) позволя-
144
ет точке В тела перемещаться вдоль некоторой линии. В шар-
нирно подвижной опоре возникает реакция RB , перпендику-
лярная направлению перемещения опоры.
Шарнирно неподвижная опора (рис. 7,а, б, опора А) не позволяет точке А никаких перемещений. В шарнирно непод-
вижной опоре возникает реакция RA произвольного направления, которую для удобства определения раскладывают на две
|
|
|
|
взаимно перпендикулярные составляющие X A |
и YA : |
||
|
|
|
|
RA |
X A |
YA . |
|
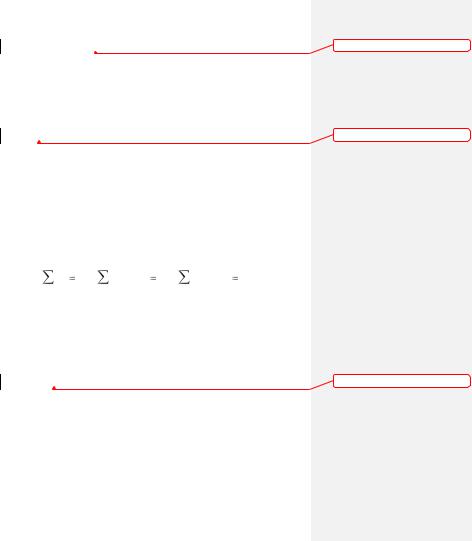
Заделка - одна из часто встречающихся связей (опор). Пусть горизонтальная одноопорная (консольная) балка (рис. 8) имеет один свободный конец, а другой конец жестко заделан в
стену. Стена воздействие на балку со-
средоточенной силой RA (реакцией) и
|
|
моментом m А, называемым реактив- |
|
|
|
ным моментом, или моментом в задел- |
|
Рис. 8 |
ке. |
||
При решении задач, выгодно пред- |
|||
|
|
||
|
|
|
|
ставлять и изображать силу RA в виде двух составляющих |
|||
|
|
|
|
сил: RA |
X A |
YA . Поэтому реакцию в заделке изображают |
|
так, как показано на рис. 8. |
|||
Теорема Вариньона |
Отформатировано |
|
Для произвольной системы сил верна теорема Вариньона: вектор момент равнодействующей любой системы сил относительно произвольной точки равен сумме векторов моментов
всех составляющих сил относительно той же точки. |
|
|||
|
|
|
|
|
M0 |
( R ) |
M0 |
( Pk ) . |
(12) |
Если все силы расположены в одной плоскости и точка О (центр моментов) находится в той же плоскости, то все векторы моменты сил будут расположены на одной прямой, проходящей через точку О, и перпендикулярной к плоскости сил, а
145

тогда, согласно (5.9), векторное суммирование можно заме-
нить алгебраическим |
|
|
M0 ( R ) |
M0 ( Pk ) . |
(13) |
Момент равнодействующей плоской системы сходящихся сил относительно произвольной точки в плоскости сил равен алгебраической сумме моментов всех составляющих сил относительно той же точки.
Момент равнодействующей произвольной системы сил относительно какой - либо оси равен алгебраической сумме
моментов всех составляющих сил относительно той же оси |
|||
|
|
|
|
M01( R ) |
M01( Pk ) . |
(14) |
|
|
|
|
1,2, ,n ) можно |
Произвольную систему сил Pk |
( k |
||
привести к некоторой точке О, называемой центром приведе- |
|||
|
|
|
|
ния и заменить одной силой - главным вектором R и одним |
|||
|
|
|
|
моментом главным моментом |
MO . |
|
|
|
|
|
|
|
Главным вектором R произвольной системы сил |
|
|
( k 1,2, ,n ) называется векторная сумма этих сил |
|
||
Pk |
|
||
|
|
|
|
|
R |
Pk . |
|
|
Главный вектор для данной системы сил величина посто- |
||
янная, не зависящая от выбора центра приведения. |
|
||
|
|
|
|
|
Главным моментом MO произвольной системы сил |
Pk |
|
( k 1,2, ,n ) называется векторная сумма моментов этих сил
|
|
|
|
|
|
|
|
|
|
|
|
M0 |
|
M0 |
( Pk ). |
|
|
|
Главный момент для данной системы сил зависит от по- |
|||||||
ложения центра приведения. |
|
|
|
|
|
|||
|
Для равновесия произвольной системы сил необходимо и |
|||||||
|
|
|
|
|
|
|
|
|
достаточно, чтобы ее главный вектор V |
и главный момент |
|||||||
|
|
|
|
|
|
|
|
|
M0 |
относительно любой точки О были равны нулю. |
|
||||||
|
|
|
|
|
|
|
|
|
|
R |
Pk |
0; |
M0 |
|
M0 |
( Pk ) 0 . |
(15) |
Для получения уравнений(15) в скалярной (координатной) форме, нужно спроецировать левые и правые части этих ра-
146

венств на оси прямоугольной декартовой системы координат и затем использовать формулу (10)
Rx= Pkx = 0, Ry= |
Pky = 0, Rz= Pkz = 0, |
|||
M Ox |
npOx M 0 ( Pk ) |
M x ( Pk ) 0 , |
||
|
|
|
|
|
M Oy |
npOy M 0 |
( Pk ) |
M y ( Pk ) 0 , |
|
|
|
|
|
|
M Ox |
npOz M0 |
( Pk ) |
M z ( Pk ) 0 . |
|
Поскольку Pkx = Xk; Pky = Yk, Pkl = Zk, получаем |
||||
X k 0; |
Yk 0; |
Zk 0; |
|
(16) |
|
|
|
||
M x ( Pk ) 0; |
M y ( Pk ) 0; |
M z ( Pk |
) 0. |
|
Итак, для равновесия произвольной системы сил необходимо и достаточно, чтобы сумма проекций всех сил системы на каждую из трех произвольно выбранных координатных осей равнялась нулю и чтобы сумма моментов всех сил системы относительно каждой из этих осей также равнялась нулю.
Система сходящихся сил |
Отформатировано |
Выберем начало координат в точке пересечения линий действия (схождения) сил. Тогда линии действия всех сил пересекают оси координат и, согласно формуле (16) моменты сил относительно этих осей равны нулю. Три последние равенства (16) принимают вид 0 = 0. Поэтому
X k 0; |
Yk 0; |
Zk 0 . |
(17) |
Итак, для равновесия системы сходящихся сил необходимо и достаточно, чтобы сумма проекций всех сил на каждую из трех координатных осей равнялась нулю.
Если все сходящиеся силы расположены в одной плоскости, то, взяв оси Ox к Oy в плоскости сил, видим, что Zk = 0, т. е. проекция любой силы на ось Oz равна нулю. Поэтому третье уравнение (17) дает тождество: 0 = 0, которое бесполезно.
Итак, для плоской сходящейся системы сил
X k 0; |
Yk 0 . |
(18) |
147
Теорема о трех силах
Для определения неизвестных сил удобно использовать теорему о трех силах: если твердое тело находится в равновесии под действием трех непараллельных сил, расположенных в одной плоскости, то линии действия этих сил пересекаются в одной точке.
Система параллельных сил, не лежащих
в одной плоскости
Проводим оси координат так, чтобы ось Oz была параллельна силам, а тем самым оси Ox и Oy будут перпендикулярны силам. Тогда все силы проецируются на ось Oz в полную величину со знаком плюс или минус в зависимости от того, совпадает ли направление силы с направлением оси, или противоположно этому направлению. Проекции всех сил на оси Ox и Oy равны нулю. Также равны нулю моменты всех сил относительно параллельной им оси Oz. Поэтому вместо уравне-
ний (16) получаем систему |
|
||
|
|
|
|
Pk |
0; |
M x ( Pk ) 0; |
M y ( Pk ) 0 . (19) |
Итак, для равновесия системы параллельных сил, не лежащих в одной плоскости, необходимо и достаточно, чтобы сумма проекций всех сил на ось, параллельную силам, равнялась нулю и чтобы сумма моментов всех сил относительно каждой из двух координатных осей, лежащих в плоскости, перпендикулярной силам, также равнялась нулю.
Произвольная плоская система сил
Выберем систему осей координат так, чтобы плоскость (х, у) совпадала с плоскостью сил. Тогда проекции всех сил на ось Oz равны нулю: Zk = 0, и моменты всех сил относительно осей Ox и Oy также равны нулю, так как эти оси и силы лежат в одной плоскости. Согласно определению момента силы относительно точки (1) и момента силы относительно оси (8) в нашем случае момент силы относительно оси Oz совпадает с момен-
148
Отформатировано
Отформатировано
Отформатировано
том этой силы относительно точки О- начала координат. По- |
|
|||||
этому из уравнений (16) остаются три уравнения |
|
|
||||
|
|
|
|
|
|
|
X k |
0; |
Yk |
0; |
M0 ( Pk ) 0 . |
(20) |
|
Итак, для равновесия произвольной плоской системы сил не- |
Отформатировано |
|||||
обходимо и достаточно, чтобы сумма проекций всех сил на |
|
|||||
каждую из двух координатных осей в плоскости этих сил рав- |
|
|||||
нялась нулю и чтобы сумма моментов всех сил относительно |
|
|||||
любой точки в плоскости этих сил также равнялась нулю. Без |
|
|||||
доказательства, отметим, что вместо уравнений равновесия |
|
|||||
(20) для плоской системы сил можно использовать уравнения: |
|
|||||
|
|
|
|
|
|
|
X k 0; |
M O1( Pk ) 0 |
M O2 ( Pk ) 0 , |
(21) |
|
||
при условии, что ось х- не перпендикулярна O1O2; |
|
|
||||
|
|
|
|
|
|
|
M O1( Pk ) 0, |
M O2 ( Pk ) |
0, |
M O3 ( Pk ) 0 , |
(22) |
|
|
при условии, что точки O1, O2, O3 не лежат на одной прямой. При решении задач можно пользоваться тремя видами
систем уравнений равновесия (20), (21), (22) исходя из конкретных условий задач. Выбор той или иной системы уравнений равновесия зависит в первую очередь от особенностей задачи, уровня знаний, опыта, желания и вкуса решающего.
Известно, что момент силы, отличной от нуля, относительно данной точки равен нулю, когда линия действия силы проходит через данную точку. Отсюда следует практический вывод: если при определении неизвестных сил нужно составить уравнения, в которые входят моменты этих сил, то за центр моментов О выгодно брать точку, через которую проходит линия действия одной или нескольких неизвестных сил.
Система параллельных сил, расположенных в одной плоскости
Если все параллельные силы лежат в плоскости х, у, то, выбирая оси так, чтобы ось Ox была перпендикулярна силам,
получим, что все Xk = 0, a Yk = Pk, где Pk – проекция силы на
ось у силы Pk . Из (20) остаются два уравнения
149
