2906

где величина k принимает те же значения, что и в формуле

(3.1).

Поперечная сила Qy , изгибающий момент M x и интенсивность распределенной нагрузки q в некотором сечении

балки связаны дифференциальными зависимостями Д.И. Журавского:

где q - интенсивность распределенной нагрузки; z – координа-

та, определяющая положение сечения балки.

Интенсивность распределенной нагрузки считается положительной, если эта нагрузка направлена вверх, в направлении оси y .

При построении эпюр Qy и M x и их контроле следует

учитывать правила, вытекающие из дифференциальных зависимостей (3.3) и непосредственно из метода сечений.

I. Если на участке балки отсутствует распределенная нагрузка q 0 , то поперечная сила Qy на этом участке постоян-

на, а изгибающий момент M x изменяется по линейному зако-

ну.

2. Если на участке балки действует равномерно распределенная нагрузка q C , то на этом участке поперечная сила С

меняется по линейному закону, а изгибающий момент M x по

закону квадратичной параболы. При этом выпуклость параболы всегда направлена навстречу распределенной нагрузке.

3. Если поперечная сила Qy меняет знак, проходя через

ноль, то в сечении, где она равна нулю, изгибающий момент принимает экстремальное значение (максимум или минимум), причем, если Qy переходит с плюса на минус, то эпюра M x

имеет максимум. В противном случае эпюра M x имеет мини-

мум.

4. В сечении, где приложена внешняя сосредоточенная си-

110

ла, на эпюре Qy должен быть скачок на величину этой силы, а на эпюре M x излом смежных участков (разрыв первой произ-

водной).

5. В сечении, где приложен внешний сосредоточенный момент, на эпюре M x должен быть скачок на величину этого

момента.

Построив эпюры поперечных сил и изгибающих моментов, определяем положение наиболее опасного с точки зрения прочности сечения балки. Если поперечное сечение балки на всей ее длине неизменно, то опасным будет то сечение, в котором изгибающий момент достигает наибольшeгo по абсолютной величине значения. В противном случае опасное сечение непосредственно по эпюре определить нельзя.

Расчет на прочность балки переменного сечения проводится на основе условия прочности по нормальным напряжениям

каемое напряжение.

Для балки постоянного сечения условие прочности по нормальным напряжениям имеет вид

где M x - изгибающий момент в опасном сечении.

Изгиб плоских рам Узлом называется жесткое или шарнирное соединение не-

скольких стержней между собой. Рамой называют стержневую систему стержни которой соединены между собой узлами, элементы которойстержни работают в основном на изгиб или кручение. Рама является плоской, если оси всех составляющих ее элементов и действующие на них нагрузки лежат в одной плоскости.

111

В общем случае в поперечном сечении плоской рамы возникают три внутренних силовых фактора: поперечная сила

Qy , изгибающий момент M x и нормальная (продольная) сила

N . Их определяют методом сечений.

При определении внутренних силовых факторов для рамы выбирают направление обхода. Раму обходят не пересекая ее стержней. Если рама имеет замкнутый контур, то обход производят находясь либо внутри контура рамы, либо вне его.

Продольная сила N в произвольном сечении численно равна взятой с обратным знаком алгебраической сумме проекций внешних сил, приложенными к части рамы, расположенной по одну сторону от рассматриваемого сечения на внешнюю нормаль к этому сечению.

Величины поперечной силы Qy и изгибающего момента M x для рамы находят также как и для балки, причем для них

сохраняется и правило знаков, и дифференциальные зависимости (3.3), и вытекающие из них следствия. При этом необходимо использовать локальную систему координат, ось у которой направлена перпендикулярно оси рассеченного стержня рамы, а ось z вдоль этой оси вправо.

Построение эпюр N , Qy и M x начинают с определения

реакций опор, за исключением рам, имеющих крепление в одной точке (консольное крепление). В этих рамах внутренние силовые факторы можно определять двигаясь от свободного конца к закрепленному. При построении эпюры изгибающих моментов положительные ординаты эпюры M x откладывают

со стороны сжатых волокон. Построив эпюры N , Qy и M x ,

выявляют опасное с точки зрения прочности сечение, в котором изгибающий момент M x достигает наибольшего по абсо-

лютной величине значения.

Проектный расчет на прочность для рамы проводят также как и для балки, используя условие прочности (3.4).

Подобранное сечение проверяют на прочность, исходя из

112

условия прочности

где N - нормальная сила, определенная по эпюре нормальных сил для опасного сечения; F - площадь опасного поперечного сечения рамы.

§14. Примеры расчета балок и рам при изгибе Пример 21. Расчет одноопорной (консольной) балки

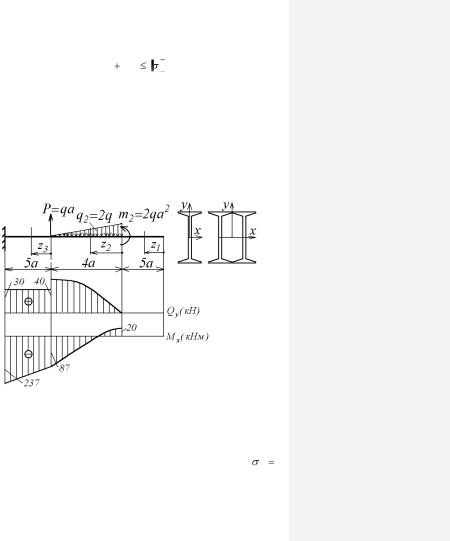
Для консольной балки, изображенной на рис 3.2, принять a 1 м, q 10 кН/м. Требуется:

Рис. 3.2

1.Построить эпюры поперечных сил для. Вычислить все характерные ординаты для этих эпюр.

2.Построить эпюры изгибающих моментов и из условия прочности подобрать размеры указанных ниже сечений приняв

225 МПа. Коэффициент запаса прочности n принять равным

1,5.

113

3. Подобрать номер прокатного двутавра и в качестве вариантасечение в виде двух одинаковых, не связанных между собой двутавров, поставленных вплотную друг к другу. Установить, какое сечение рациональнее, сравнив коэффициенты

экономичности сечений k Wx / F 3 , где Wx - момент сопро-

тивления сечения относительно нейтральной оси; F - площадь сечения.

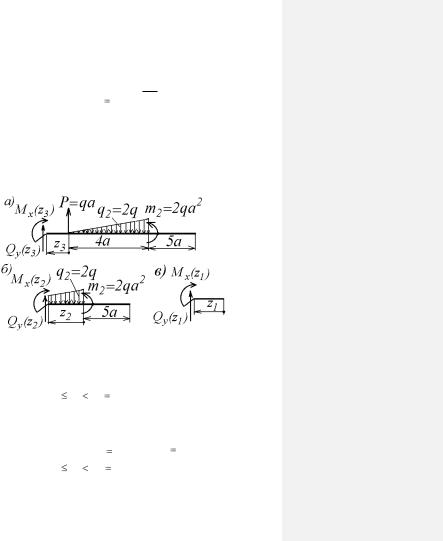
Решение В консольной балке, показанной на рис. 3.2, можно выде-

лить три участка непрерывного изменения поперечных сил и изгибающих моментов. Определим поперечные силы и изги-

Рис. 3.3

бающие моменты для этих участков, сечений. Удобнее рассматривать участки в порядке справа налево, так как при этом не возникнет необходимости определять реакции заделки.

Участок 1: 0 z1 a3 5a .

Как видно из рис. 3.3, а, на этом участке к балке не приложено никаких нагрузок. Поэтому поперечные силы и изгибающие моменты на всем участке равны нулю.

Qy ( z1 ) 0 , M x ( z1 ) 0

Участок 2: 0 z1 a2 4a .

114

На этом участке (рис. 3.3, б,) на балку действует распределенная нагрузка, которую можно описать формулой

2q

q( z2 ) 4a ( 4a z2 ) q( 4a z2 ) / 2a .

Закон распределения поперечной силы на этом участке найдем исходя из теоремы Журавского

При определении Qy ( z2 ) учтено, что распределенная на-

грузка, направленная противоположно оси у, считается отрицательной.

которая получается на основе геометрических соображений. Величина Qy ( z2 ) численно равна площади трапеции, соответ-

ствующей графику распределенной нагрузки (рис. 3.4). Исходя из той же теоремы

Qy ( z2 ) dMx / dz2

115

найдем изгибающий момент, учитывая, что в точке z2 0 приложен момент m2

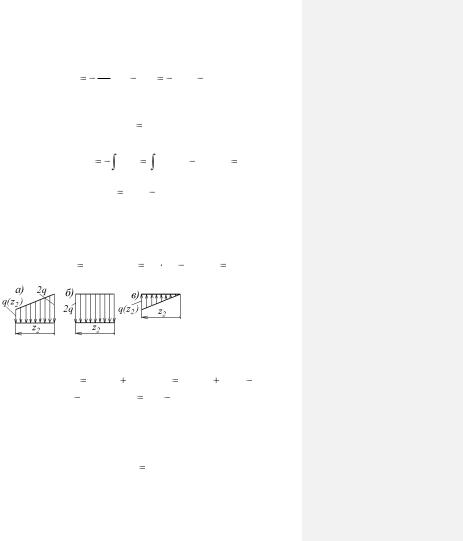
При определении момента распределенной нагрузки, изменяющейся по закону трапеции (рис. 3.4, а), нагрузку удобно представить в виде суммы постоянной составляющей

q2 2q (рис. 3.4, б) и переменной составляющей q( z2 ) 2qz2 / 4a (рис. 3.4, в).

Изгибающий момент постоянной составляющей относительно оси сечения равен

M x ( z2 ) 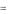2qz2 0,5z2 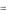qz22 .

Изгибающий момент переменной составляющей относительно оси сечения равен

ложенную в точке, удаленной от рассматриваемого сечения на

В результате, поперечная сила на третьем участке будет равна

Qy (z3 ) 4qa - qa 3qa .

Изгибающий момент на этом участке определяется силой Р и плечом z3 , равнодействующей R, ее плечом b и моментом m2:

Эпюры поперечных сил и изгибающих моментов показаны на рис. 3.2. Из них видно, что максимальное значение изгибающего момента M x max 2,367 105 Нм достигается в заде-

ланном сечении. Допускаемое напряжение

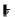
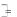Tp / n 225 / 1,5 150МПа .

Исходя из условий прочности, подберем размеры указанных сечений

1,578 106 мм3 1578 см3 .

Этому значению соответствует двутавр с профилем №50 с площадью сечения 97,8 см2 и моментом сопротивления

Wx 1670 см3. Для каждого из двух одинаковых двутавров момент сопротивления составит

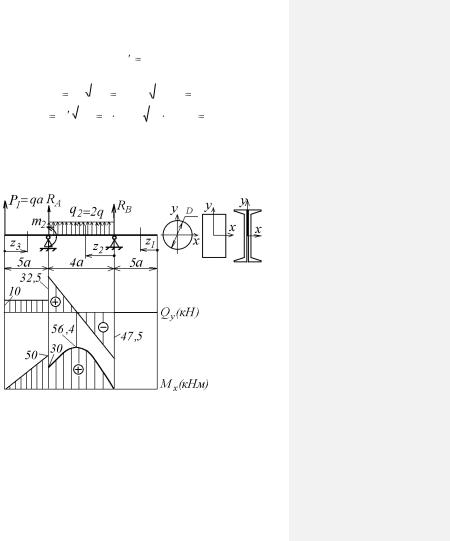
что соответствует профилю № 40 с площадью сечения 71,4 см2 и моментом сопротивления Wx 947 см3. Для этих двух случаев коэффициенты экономичности составят соответственно

Следовательно, в данном случае рациональнее использовать сечение, состоящее из одного двутавра.

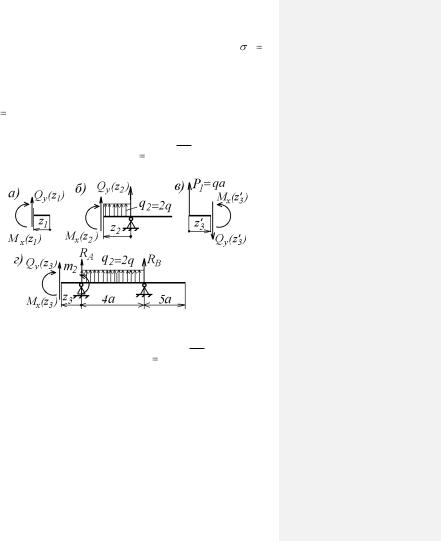
Пример 22. Расчет двухопорной балки

Рис. 3.5 Для двухопорной балки, изображенной на рис 3.5 принять

a 1 м; q 10 кН/м. Требуется:

1.Построить эпюры поперечных сил. Вычислить все характерные ординаты для этих эпюр.

2.Построить эпюры изгибающих моментов и из условия прочности подобрать размеры указанных ниже сечений приняв

118

225 МПа. Коэффициент запаса прочности n принять равным

1,5.

3. Подобрать диаметр d сплошного круглого сечения, размеры b и h прямоугольного сечения с отношением сторон h / b 1,5 и сечение в виде двух одинаковых, не связанных между собою швеллеров, поставленных вплотную друг к другу. Установить, какое сечение рациональнее, сравнив коэффи-

циенты экономичности сечений k Wx / F 3 .

Рис. 3.6

Установить, какое сечение рациональнее, сравнив коэффициенты экономичности сечений k Wx / F 3 , где Wx - мо-

мент сопротивления сечения относительно нейтральной оси; F - площадь сечения.

Решение Двухопорная балка, показанная на рис. 3.5, является ста-

тически определимой системой, поэтому можно найти реакции ее связей методами теоретической механики. Для этого заменим действие на балку имеющихся связей неизвестными реакциями (рис. 3.5)

Составим уравнение равновесия моментов относительно точки А для определения реакции RB

119