2906

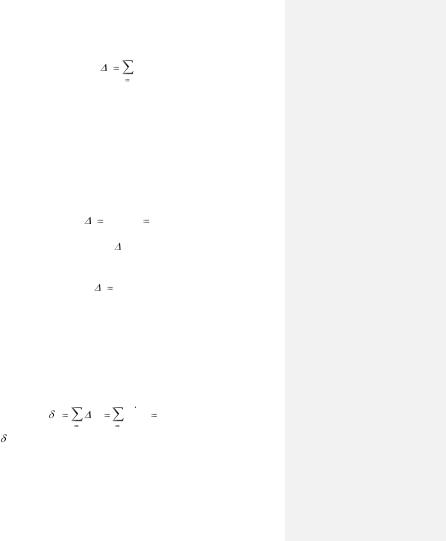
пределах выполнения закона Гука определяется по формуле

где n - количество участков; N i , Ei , Fi - нормальная сила,

модуль Юнга и площадь поперечного сечения i - го участка. Жесткостью стержня называется величина

C=EF/l, (1.8)

где Е - модуль упругости материала стержня, F и l - площадь поперечного сечения и длина стержня.

Жесткость стержня численно равна силе, увеличивающей длину стержня на единицу длины. По определению С измеряется в Н/м.

Нормальная сила в стержне определяется из выражения

Если по длине стержня нормальная сила изменяется линейно, то удлинение стержня определяется по формуле

где N * - средняя сила, равная половине суммы нормальных сил на концах стержня (или его части, для которой определяется удлинение).

Если стержень состоит из нескольких стержней, материалы и сечения которых различны, то для определения жесткости C всего стержня приложим на его концах растягивающие единичные силы. Тогда в стержне будет действовать нормальная сила, равная 1 и

где i - растяжение стержня, вызванное единичной силой; li, Ei, Fi - длина, модуль упругости материала и площадь сечения i- той части стержня; n - число этих частей.

Поскольку Сi- жесткость i - той части стержня, и

85

li/EiFi=1/Ci,

постольку

Вычисленную подобным образом жесткость называют эквивалентной жесткостью.

Если нужно определить жесткость какой-либо части стержня, можно использовать (1.11), где n должно быть равно числу участков стержней, входящих в эту часть стержня.

Для определения перемещения некоторой точки А, зависящего от нескольких параллельных друг другу БП, можно воспользоваться методом суперпозиции перемещений, суммируя перемещения этой точки, вызванные каждым БП. Тогда

где l ij, N ij - удлинение и нормальная сила для стержня i, вызванные БП с номером j.

Если некоторая точка А участвует одновременно в двух перемещениях вдоль осей системы координат, то полное перемещение этой точки определяется по формуле

где АХ, АY- перемещение вдоль осей X и Y.

При использовании МБП следует помнить, что принцип суперпозиции перемещений, на котором основан МБП, применим при достаточно малых перемещениях, когда напряжения в стержнях не превышают пределы пропорциональности материалов стержней. Поэтому при составлении уравнений равновесия и схем перемещений можно считать размеры деформированной системы равными размерам этой системы до деформации (принцип начальных размеров).

Метод базовых перемещений имеет ряд весьма ценных достоинств.

Следует отметить, что метод базовых перемещений применим и к стержневым шарнирным системам, содержащим произвольное количество стержней и твердых тел.

Методы, использующие уравнения совместности перемещений, не удобны потому, что требуют построения картины перемещений и учета специфики деформирования систем.

Метод базовых перемещений позволяет формализовать составление уравнений совместности перемещений. При большом количестве стержней метод позволяет значительно понизить порядок разрешающих уравнений. Метод не требует построения картины перемещений стержней и тел системы, что особенно удобно при рассмотрении пространственных систем.

Традиционные методы расчета рассматриваемых систем, основанные на энергетических соотношениях и использующие

87

канонические уравнения метода сил, требуют очень громоздких выкладок и приводят к разрешающим системам уравнений, количество которых равно количеству стержней в системе.

§ 4. Алгоритм решения задач МБП При использовании МБП для решения задач сопротивле-

ния материалов нет необходимости определять степень статической неопределимости системы, поскольку количество правильно выбранных БП всегда равно количеству независимых уравнений статики. Поэтому исчезает различие между статически определимыми и неопределимыми системами. Это в значительной мере упрощает алгоритм решения задач. Решение задач сопротивления материалов МБП ведется в следующем порядке:

1.Определить количество узлов и дисков.

2.Выбрать нужное число узлов и точек дисков и задать БП для этих узлов и точек . БП для дисков должны удовлетворять связям, наложенным на диски, если таковые имеются. Если какая-либо точка диска неподвижна, то БП для диска будет или его угол поворота относительно точки закрепления, или перемещение некоторой его точки, направленное перпендикулярно радиусу, соединяющему эту точку с точкой закрепления.

3.Разорвав стержни системы и заменив их действие на диски или узлы нормальными силами, записать уравнение равновесия узлов и дисков. Нормальные силы удобно выбирать растягивающими, то есть направленными от узлов или дисков. Число уравнений равновесия узла или диска должно быть равно числу его БП W.

4.Выразить нормальные силы в стержнях через жесткости

ибазовые перемещения.

5.Подставить нормальные силы в уравнения равновесия.

6.Решить уравнения равновесия относительно БП.

7.Определить нормальные силы в стержнях.

8.Проверить правильность решения подстановкой величин нормальных сил в уравнения равновесия.

88

Ниже рассмотрены примеры решения различных задач МБП, демонстрирующие возможности метода.

§5. Примеры решения задач МБП для плоских систем

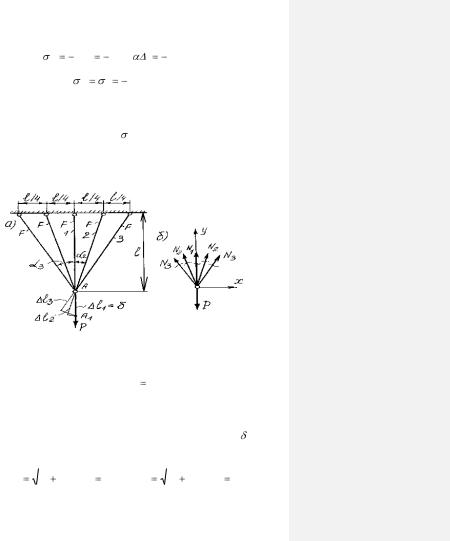
Пример 1. Раскрытие статической неопределимости ступенчатого стержня

Стальной ступенчатый стержень закреплен с обоих концов при нормальной температуре и нагружен сосредоточенной силой P=14qa и равномерно распределенной нагрузкой q (рис.

1.2, а).

Требуется:

а) построить эпюры нормальных сил N и нормальных на-

Решение Система один раз статически неопределима, поскольку для

стержня можно составить только одно уравнение равновесия

Piz 14qa 4q2a RA RB 0 ,

содержащее две неизвестные реакции RA и RB. Отсюда следует

RA + RB - 6qa =0.

Стержень имеет три участка непрерывного изменения нормальных сил, ограниченных концевыми сечениями стержня и точками скачкообразного изменения площади поперечного сечения стержня.

При отсутствии реакции RB перемещение точки В равно

89

3

p lip ,

i 1

сила постоянная величина и li Ci Nip* для участков, в пре-

90

делах которых нормальная сила переменная величина; N ip* -

средняя нормальная сила сила для участка i. Индекс p указывает, что сила Nip и удлинение lip вызваны действием только внешних нагрузок.

Для определения Nip используем метод сечений, для чего стержень рассекается в нужном месте поперечным сечением, отбрасывается какаялибо из его частей вместе с приложенными к ней нагрузками, ее действие на рассматриваемую часть стержня заменяется нормальной силой Nip, направленной в сторону отброшенной части. Силу Nip определяют из уравнения равновесия рассматриваемой части.

где СВ- жесткость всего стержня; NR - нормальная сила, вызванная действием RB.

91

По определению

RA 6qa RB 6 80 0,5 171,429 68,571 кH .

В соответствии с принципом суперпозиции определяем нормальные силы в стержнях, вызванные внешними силами и реакцией RB по формуле

По полученным значениям Ni строим эпюру нормальных сил в масштабе 20 кН/мм (рис. 1.2, б).

Для определения нормальных напряжений используем формулу

92

* 0,5 / 13100 17,58 МПa ,

При изменении температуры стержней удлинение участка стержня определяется по формуле

где - коэффициент температурного расширения материала участка; t - изменение температуры в сравнении с проектной температурой.

Для определения нормальных сил и напряжений, вызванных воздействием температуры, стержень освобождается от внешних нагрузок и оказывается только под действием реак-

ций RAt и RBt (рис. 1.2, г). Из уравнения равновесия стержня

При отсутствии заделки конца В в сечениях стержня нормальные силы будут отсутствовать и его перемещение будет результатом температурного расширения

Перемещение точки В, вызванное реакцией RBt , будет

равно - В, поскольку перемещение конца стержня в заделке равно нулю. Тогда

Как и следовало ожидать, напряжения оказались сжимающими.

По полученным значениям напряжений строим эпюру температурных напряжений (рис. 1.2, д).

Пример 2. Определение перемещений в статически неопределимой пятистержневой системе

Рис. 1.3

Определить перемещение точки приложения силы Р и нормальные силы в стержнях системы, изображенной на рис.

1.3, а, если Р= 200 кН; l =1 м; E 2 105 МПа ; F=1 см2.

Решение Система симметрична относительно вертикальной оси и

поэтому три раза статически неопределима. Перемещения в системе определяются одним базовым перемещением , поэтому система один раз кинематически определима.

Длины стержней