
2614
.pdf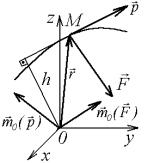
упадет обратно на Землю. Все эти результаты относятся к движению в безвоздушном пространств.
|
|
|
9.8. Теорема об изменении момента |
|||
|
|
|
импульса точки (теорема моментов) |
|||
|
|
Из двух основных динамических характеристик, введен- |
||||
ных в 9.1, величина p mv |
является векторной. Иногда при |
|||||
|
|
|
|
изучении движения точки вместо векто- |
||
|
|
|
|
ра |
p |
необходимо рассматривать его |
|
|
|
|
момент. Момент вектора p относитель- |
||
|
|
|
|
но данного центра О или оси z обознача- |
||
|
|
|
|
ется |
mpo m0 p или mpz =mz p и на- |
|
|
|
|
|
зывается соответственно моментом им- |
||
|
|
|
|
пульса (кинетическим моментом) точки |
||
|
|
|
|
относительно этого центра (оси). Вы- |
||
|
|
|
|
числяют момент вектора p так же, как и |
||
|
|
|
Рис. 9.17 |
момент силы, считая вектор p прило- |
||
|
|
|
женным к движущейся точке. Модуль |
|||
|
|
|
|
|||
|
|
mgh, где h - длина перпендикуляра, опущенного из цен- |
||||
|
|
|||||
|
mpo |
|
||||
тра О на направление вектора p (рис. 9.17).
9.8.1. Теорема о связи моментов относительно оси Пусть материальная точка массы m движется под действи-
ем силы F . Момент вектора F относительно некоторой неподвижной оси z,
|
|
|
|
|
mz F xFy yFx . |
|
|
|
|
(9.20) |
|||||
Аналогично для величины mz mv , будет |
|
|
|
||||||||||||
|
|
|
|
mz p mz mv m xvy yvx . |
|
|
(9.21) |
||||||||
Тогда |
|
|
|
|
|
|
|
|
dvy |
|
|
|
|
||
|
d |
|
|
dx |
|
dy |
|
|
|
|
dv |
x |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
mz |
mv m |
vy |
|
vx |
|
|
ym |
|
|
||||
|
dt |
dt |
xm |
dt |
dt |
. |
|||||||||
|
|
|
dt |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
110 |
|
|
|
|
|
|
||

В правой части полученного выражения первая скобка
равна нулю, так как dx vx , а dy vy . Вторая скобка, соглас- dt dt
но (9.20), равна mz F , так как по основному закону динамики
Тогда
d
dt
m |
dvy |
F |
y |
и m |
dvx |
F . |
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
dt |
|
|
|
dt |
|
|
x |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
d |
|
|
|
|
|
|
|
||
mz mv |
mz m |
|
|
|
v |
|
mz |
F |
. |
(9.22) |
|||||
dt |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Полученное соотношение выражает теорему моментов относительно оси: производная по времени от момента импульса точки относительно некоторой оси равна моменту действующей силы относительно той же оси.
Аналогичная теорема верна и для моментов относительно любого центра О (см. формулу 9.24)
Из (9.22) следует, что если mz F 0, то mz mv const, т. е. если момент действующей силы относительно некоторой оси равен нулю, то момент импульса точки относительно этой оси постоянен.
9.8.2. Теорема моментов относительно центра Пусть материальная точка движется под действием силы
F и имеет импульс mv . Момент силы относительно точки (центра) О m0 F r F . Аналогично m0 mv r mv .
Вектор m0 F (рис. 9.17) направлен перпендикулярно плоскости проходящей через векторы F и r , а вектор m0 mv
- перпендикулярно плоскости, проходящей через векторы mv иr . Очевидно, что
d |
|
|
dr |
|
|
|
dv |
|
|
|
|
|
||
|
r |
mv |
|
|
mv |
r m |
|
|
v |
mv |
r |
ma |
. |
|
dt |
|
dt |
||||||||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|||
111

Поскольку векторное произведение двух параллельных векторов равно нулю, v mv 0 и ma F
d
dt
или
d
dt
r mv r |
|
F . |
m0 mv m0 F .
(9.23)
(9.24)
Итак, доказана следующая теорема моментов относительно центра: производная по времени от момента импульса точки относительно некоторого неподвижного центра, равна моменту действующей на точку силы относительно того же центра.
Аналогичная теорема верна и для моментов вектора mv и
силы F относительно некоторой оси z, в чем можно убедиться, проецируя обе части (9.24) на эту ось. Математически теорема моментов относительно определяется по (9.22).
Из сравнения (9.24) и (12.4) видно,
что моменты векторов mv и F связаны такой же зависимостью, какой связаны
сами векторы mv и F . |
|
|
Из (9.24) |
следует, что |
если |
m0( F ) 0, то |
m0(mv )= const, т. |
е. если |
момент действующей силы относительно некоторого центра равен нулю, то мо-
мент импульса точки относительно этого центра постоянен.
Задача 9.8. Шарик М привязан к нити (рис. 9.18) МВА, часть ВА которой продета сквозь вертикальную трубку. В момент, когда шарик находится на расстоянии h0 от оси z трубки, ему сообщают начальную скорость v0 , перпендикулярную к плоскости МВА. Одновременно нить начинают медленно втя-
112
гивать в трубку. Найти, какую скорость v1 будет иметь шарик, когда его расстояние от оси z станет равно h1.
Решение. На шарик действует сила тяжести G mg и ре-
акция нити |
N . Моменты этих сил относительно оси z равны |
|||||||
нулю, так как сила G параллельна оси z, |
а сила N эту ось пе- |
|||||||
ресекает. |
Согласно |
(9.22), |
|
d |
mz mv 0, |
откуда |
||
|
|
|||||||
mz mv mvh const. |
|
|
|
dt |
m постоянна, то |
|||
Так |
как |
масса |
||||||
v0h0 v1h1 . Следовательно, |
v1 h0v0 / h1, |
то есть по мере при- |
||||||
ближения шарика к оси вращения его скорость растет. |
|
|||||||
9.9.Задачи для самостоятельного решения
9.9.1.Вагонетка, масса которой вместе с полезной нагрузкой m = 100 кг, при движении по горизонтальному пути испытывает сопротивление, величина которого составляет 0,01 от всех вертикальных нагрузок. Рабочий толкает вагонетку с горизонтальной силой F = 200 Н. Через какое время рабочий сообщит вагонетке скорость v = 0,6 м/сек?
9.9.2.На тело массой m = 2 кг, находящееся в покое на
горизонтальной плоскости, действует вертикальная сила F , возрастающая от нуля пропорционально времени с коэффициентом пропорциональности k 2 н/с. Через сколько времени
после начала действия силы F тело начнет двигаться? Найти закон этого движения.
9.9.3. В тот момент, когда скорость моторного судна массы m равна v0 , мотор выключается, и судно движется, испы-
тывая сопротивление воды, величина которого пропорциональна скорости. Коэффициент пропорциональности между силой сопротивления и скоростью равен ; масса судна равна m . Через какой промежуток времени скорость судна уменьшится вдвое?
9.9.4. Определить, пользуясь теоремой об изменении импульса, время, в течение которого тело, брошенное под углом
113

0 к горизонту с начальной скоростью v0 , достигает макси-
мальной высоты.
9.9.5. На материальную точку массой m = 2 кг действует сила, проекции которой на координатные оси, выраженные в Н, равны:
X 6cos2t; Y 6 sin2t ; Z 6 sin2t ,
где t - время в с. Определить скорость v2 точки в момент времени t2 = = 3,14 с, если в момент времени t1= /2 ее
скорость v1 |
имеет модуль 2 м/с и составляет с координатными |
|||
осями x , y , |
z углы, равные соответственно 30 , 60 и 90 . |
|||
|
|
9.9.6. Решить задачу 9.4, учиты- |
||
|
|
вая сопротивление воздуха, величина |
||
|
|
которого |
выражается |
формулой |
|
|
R kmgv |
где k - постоянный коэф- |
|
|
|
фициент, |
m - масса тела, v - его ско- |
|
|
|
рость. |
|
|
|
|
9.9.7. Материальная |
точка М |
|
|
|
перемещается по шероховатому кри- |
||
|
|
волинейному желобу, расположен- |
||
Рис. 9.19 |
ному в вертикальной плоскости xOy , |
|||
под действием собственной силы тяжести. Угол трения равен. Начальная скорость этой точки, когда она занимает положение А, составляет с вертикальной осью Оу угол и по модулю равна v0 , а ее конечная скорость
в точке В направлена по горизонтальной оси Ох и по модулю равна v. Найти импульс нормальной реакции
Nжелоба за промежуток времени t,
втечение которого, точка М пере-
местилась из А в В (рис. 9.19). |
Рис. 9.20 |
|
|
9.9.8. Точка М описывает эллипс под действием цен- |
|
тральной силы F (рис. 9.20). Скорость в вершине А равна v0 . 114

|
Найти скорость v в вершине В, если |
|
|
ОА= a и ОВ = b . |
|
|
9.9.9. Точка М массы |
m опи- |
|
сывает окружность радиуса |
a , при- |
|
тягиваясь точкой А этой окружности |
|
|
(рис. 9.21). В начальный момент |
|
|
точка находится в положении В и |
|
Рис. 9.21 |
имеет скорость v0 . Определить ско- |
|
рость v точки и силу притяжения F как функции вектора - радиуса r.
9.9.10.Вдоль тяги, при помощи которой тянут вагончик по горизонтальному пути, действует постоянная сила F = 250 Н. Тяга образует со скоростью угол = 32°. Определить работу, совершенную силой F на пути s = 200 м.
9.9.11.Тело массой m = 2 кг передвигают по горизон-
тальному полу при помощи горизонтальной силы на расстояние s = 6 м. Определить работу, которую совершит при этом сила трения, если коэффициент трения между поверхностью тела
иполом f = 0,35.
9.9.12.Найти работу силы
тяжести при перемещении мате-
риальной точки |
из |
положения |
M0(x0 ,y0 ,z0 ) |
в |
положение |
M( x,y,z ), а также вычислить по-
Рис. 9.22
тенциальную энергию точки в положении М (рис. 9.22). 9.9.13. Определить работу силы упругости растянутого стержня, к концу которого подвешен груз М, при перемещении этого груза из положения M0 , для которого деформация пружи-
ны равна x0 , в положение M , для которого деформация пру-
жины равна x , если длина недеформированного стержня равна l0 ; вычислить также потенциальную энергию точки в по-
ложении M .
115

9.9.14. На материальную точку действует сила, проекции которой на координатные оси определяются выражениями
X 2x y ; Y x z2; Z 2yz 1;
Определить работу этой силы при перемещении точки из положения M0 (1; 2; 3) в положение M1 (2; 3; 4), если сила выражена в Н, а координаты - в см.
9.9.15.Определить работу центральной силы, модуль которой является функцией расстояния материальной точки от центра этой силы, т. е. F f(r ).
9.9.16.Один конец пружины закреплен шарнирно в точке О, а к другому концу ее прикреплен шарик. Длина нерастяну-
той пружины -l0 , жесткость ее c. Шарик перемещают из по-
ложения M1 в положение M2 , причем пружина растягивается, поворачивается, но не изгибается. Определить работу силы упругости пружины, если OM1 r1 и OM2 r2 .
9.9.17. Колесо радиуса R катится без скольжения по горизонтальному рельсу. Найти работу трения качения при перемещении центра колеса O на расстояние s, если вертикаль-
ная нагрузка на ось колеса равна P и коэффициент трения качения равен fk .
9.9.18. К валу длиною l, один конец которого закреплен жестко, приложен на свободном конце момент, который вызывает в вале деформации кручения. Определить работу возникающих при этом сил упругости, если суммарный момент упругих сил пропорционален углу закручивания; причем коэффициент пропорциональности (коэффициент жесткости вала на кручение) равен c. Определить также потенциальную энер-
гию этого вала в зависи-
|
мости от угла закручива- |
|
ния. |
|
9.9.19. Для опреде- |
Рис. 9.23 |
ления сил натяжений T1, |
|
и T2 ветвей конвейерной |
|
116 |

ленты привод А конвейера установлен на катки и включен динамометр D между приводом и неподвижной стойкой С. Определить силы натяжения T1, и T2 , если показание динамометра равно P (в ньютонах), диаметр приводного барабана d , потребляемая электродвигателем привода мощность равна N
иприводной барабан делает n оборотов в минуту (рис. 9.23).
9.9.20.Найти мощность машины, поднимающей 100 раз в минуту молот массой m = 1000 кг на высоту h 0,6 м, если коэффициент полезного действия = 0,8.
9.9.21.Вагонетка движется самокатом вниз по наклонной плоскости, образующей с горизонтом угол . Определить скорость вагонетки в конце пути, длина которого, равна l; на-
чальная скорость вагонетки v0 = 0, коэффициент общего со-
противления движению f .
9.9.22. Телу массой m , лежащему на горизонтальной плоскости, сообщают начальную горизонтальную скорость v0 .
Определить время, пройденное телом до остановки, и расстояние, пройденное телом, если коэффициент трения тела о плоскость равен f ?
9.9.23. Клеть массой m опускается на канате равномерно со скоростью v0 . Определить наибольшее удлинение каната после защемления его верхнего конца, если его статическое удлинение под действием веса клети равно * .
9.9.24. В момент, когда скорость моторного судна равна v0 выключается мотор. Сила сопротивления воды определяет-
ся по эмпирической формуле: R av bv2, где a и b - постоянные. Масса судна равна m . Найти расстояние, которое пройдет судно с момента выключения мотора до остановки.
9.9.25. Материальная точка массы m , получив начальную скорость v0 движется по горизонтальной, абсолютно гладкой плоскости, испытывая сопротивление среды, опреде-
ляемое формулой R km
 v , где v - скорость точки. Найти
v , где v - скорость точки. Найти
117

закон движения точки.
9.9.26. Определить для данного момента времени высоту h подъема тела М, брошенного под углом к горизонту с начальной скоростью v0 , если в этот момент известен угол ,
образуемый скоростью v с горизонтальной осью x . Сопротивлением воздуха пренебречь.
9.9.27. Материальная частица массы m = 90 г, находящаяся в поле силы тяжести, отталкивается от неподвижного центра О силой, обратно пропорциональной квадрату расстояния частицы от этого центра. В начальный момент времени частица находится в положении M0 (x0 =1 см; y0 = z0 = 2
см) и имеет скорость v0 = 28
 5 см/с, направленную так, что при дальнейшем движении частица проходит через точку M1
5 см/с, направленную так, что при дальнейшем движении частица проходит через точку M1
( x1 =2 см; y1 = z1 = 4 см). Опре-
делить скорость частицы в точке M1, если известно, что величина отталкивающей силы в момент, когда частица находится в поло-
жении M0 равна 0,03 Н.
Рис. 9.24
9.9.28. Автомобиль массой m , имеющий в положении M1, скоростью v1, (рис. 9.24), начинает с этого положения движение самокатом и в положении M2 приобретает скорость v2. Определить суммарную работу сопротивлений движению автомобиля на участке M1M2, а также среднюю величину приведенной к центру тяжести автомобиля силы сопротивления движению. Высоты H1 и H2 даны в метрах.
118

Глава 10. НЕСВОБОДНОЕ И ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ
10.1. Уравнения движения точки по заданной неподвижной кривой
Несвободным движением материальной точки или движением, подчиненным связям, называется движение, сопровождающееся постоянным взаимодействием тела с некоторыми связями.
Некоторые задачи несвободного движения можно решать с помощью общих теорем
Рис. 10.1
динамики. Рассмотрим другой метод реше-
ния этих задач, применимый при любых действующих силах и позволяющий одновременно находить и закон движения точки, и реакции связей.
Пусть материальная точка движется по заданной гладкой
неподвижной кривой под действием активных сил F1a,F2a, ...,
Fna. Определим положение движущейся точки М криволиней-
ной координатой с началом отсчета в точке О (рис. 10.1).
Если, отбросив связь и заменить ее действие реакцией N , то основной закон динамики примет вид
|
a |
|
(10.1) |
ma Fk |
N . |
||
Пусть M - касательная |
в точке М, направленная в сторо- |
||
ну положительного отсчета , Mn - главная нормаль, направленная к центру кривизны кривой в точке M , а Mb - ось, перпендикулярная к ним, называемая бинормалью. Спроецируем обе части равенства (10.1) на эти оси. Так как кривая гладкая,
то реакция N перпендикулярна к кривой, т. е. расположена в
плоскости Mbn и, следовательно, N = 0. Тогда
a |
a |
a |
Nb . |
ma Fk |
, man Fkn |
Nn , mab Fkb |
|
|
119 |
|
|
