
Практикум по высшей математике: векторная алгебра и аналитическая геометрия. Пантелеев И.Н
.pdf
y +1 = − |
3 |
(x −3), 3x +4 y −5 |
= 0. |
|
4 |
|
|
Пусть х, у текущие координаты |
точки на искомой |
||
прямой, тогда расстояние от этой точки до прямой, проходящей через точку А, находится по формуле
d = Ax + By +C . A2 + B2
Подставляя |
сюда значение |
d = 3 и коэффициенты |
||||||
А,В,С, находим |
3 = |
|
3x +4 y −5 |
|
|
или, раскрывая |
модуль, |
|
|
|
|
||||||
5 |
||||||||
|
|
|
|
|
|
|||
15 = 3x +4 y −5 и 15 = 3x −4 y +5 |
|
|
||||||
Отсюда имеем 3x +4 y −20 = 0 и 3x +4 y +10 = 0. |
||||||||
4.6. Через |
|
|
точку |
пересечения |
прямых |
|||
2x − y +3 = 0 и x + y −2 = 0. |
провести |
прямую, |
||||||
перпендикулярную прямой 3x −4 y −7 = 0.
Решение. Пользуясь уравнением (9), запишем уравнение пучка прямых, проходящих через точку пересечения данных прямых
2x − y +3 +λ(x + y −2)= 0 или (2 +λ)x +(λ −1)y +3 −2λ = 0.
Угловой коэффициент пучка прямых k = − |
2 +λ |
, а угловой |
|||||||||
λ −1 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
коэффициент перпендикулярной прямой |
k |
= 3 . |
По условию |
||||||||
|
|
|
|
|
|
|
1 |
4 |
|
||
|
|
|
|
|
|
2 +λ |
|
|
|||
перпендикулярностиk = − |
1 |
, |
откуда |
= |
3 , а λ =10 |
||||||
|
λ −1 |
||||||||||
|
k |
|
|
|
|
4 |
|
||||
1 |
|
|
|
|
|
|
|
|
|
||
Подставляя найденное значение λ |
в уравнение пучка, |
||||||||||
получаем уравнение искомой прямой |
12х+9 у−17 = 0 . |
||||||||||
4.7. Даны две вершины треугольника А(-4;2) и В(2;-5) и |
|||||||||||
|
|
|
8 |
; −2 |
|
Найти третью вершину С |
|||||
точка пересечения высот М |
3 |
. |
|||||||||
|
|
|
|
|
|
|
|
|
|
||
и расстояние ее от биссектрисы угла А.
111

Решение. По уравнению прямой, проходящей через две
точки A и В, находим |
y −2 |
|
= |
x +4 |
, |
y = − |
7 x − |
8 . |
−5 −2 |
|
|||||||
|
2 +4 |
|
|
6 |
3 |
|||
Используя условие |
|
перпендикулярности (7), из |
||||||
уравнения пучка прямых (8) находим уравнение перпендикуляра МС к прямой АВ, проходящего через точку М
|
6 |
|
8 |
|
|
|
|
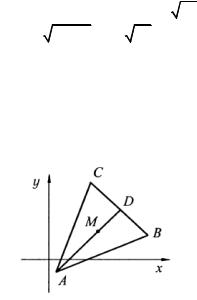
(рис. 3.23) y +2 = |
|
x − |
|
|
, |
6x −7 y −30 = 0. |
|
7 |
3 |
||||||
|
|
|
|
|
Рис. 3.23
Уравнение перпендикуляра ВМ к прямой АС находим по уравнению прямой проходящей через две точки В и М
y +5 |
= |
x −2 |
, |
y = − |
9 x −14. |
|
−2 +5 |
|
|||||
8 |
−2 |
|
|
2 |
||
|
3 |
|
|
|
||
Учитывая, что прямые АС и ВМ перпендикулярны (7), из уравнения пучка прямых, проходящих через точку А, находим уравнение стороны АС
y −2 = − 2 (x +4), 2x +9 y −10 = 0. |
|
|
9 |
Решая совместно уравнения прямых АС и МС, находим |
|
координаты точки C (5;0). Подставляя уравнения сторон АВ и |
|
AC в формулу (12), находим уравнение биссектрисы угла А |
|
7x +6 y +16 |
= − 2x +9 y −10 , 3x +5y +2 = 0. |
49 +36 |
4 +81 |
Расстояние точки С от биссектрисы находим по формуле (11)
112
d = |
|
3 5 +5 0 +2 |
|
= |
17 |
= |
34 |
. |
|
|
|||||||
|
− 9 +25 |
|
34 |
2 |
||||
|
|
|
|
|
|
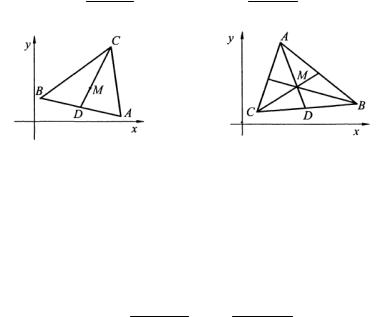
4.8. Пересечение медиан в точке M (3;3), а x − y −2 = 0 и 7x − y −8 = 0 - уравнения двух сторон треугольника. Найти
уравнение третьей стороны.
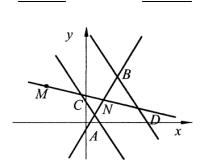
Решение. Найдем точку пересечения известных сторон треугольника и обозначим ее за A (рис. 3.24)
|
|
Рис. 3.24 |
|
|
|
x − y −2 |
= 0, |
x =1, y = −1. |
Точка пересечения |
медиан |
|
|
|
||||
7x − y −8 = 0, |
|
|
|
|
|
делит их в отношении 2:1, поэтому AM : MD = 2 :1, |
отсюда |
||||
λ = 2 |
|
|
|
|
|
xD = (1+λ)xM − xA = |
3 3 −1 = 4, yD |
= (1+λ)yM − yA = 3 3 +1 = 5. |
|||
λ |
|
2 |
λ |
|
2 |
Координаты точек C и B удовлетворяют уравнениям |
|||||
прямых AC и AB |
|
|
|
|
|
|
7xc − yc −8 = 0, и xB − yB −2 = 0. |
|
|
||
Точка |
D делит отрезок CB пополам |
xc + xB = xD =8, |
|||
yc + yB = 2 yD =10. |
|
|
|
|
|
Решая |
эти |
четыре |
уравнения |
относительно |
|
xC , yC , xB , yB , |
находим координаты точек C и B : |
|
|||
|
|
xC = 2, yC = 6, xB = 3, yB = 4. |
|
|
|
|
|
113 |
|
|
|
Используя уравнение прямой, проходящей через две точки, находим уравнение прямой BC
|
y −4 |
= |
x −6 |
, x +2 y −14 = 0. |
|
||
|
6 −4 |
2 −6 |
|
||||
|
|
|
|
|
|
||
4.9. Через точку |
|
−3; |
5 |
провести прямую |
так, |
||
M |
|
||||||
|
|
|
|
|
2 |
|
|
чтобы середина ее отрезка между прямыми 2x + y −3 = 0 и 2x + y −5 = 0 лежала на прямой 2x − y −1 = 0 .
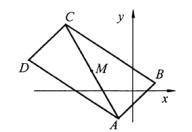
Решение. Проведем параллельные прямые на плоскости Oxy (рис. 3.25) и найдем точки пересечения A, B с
третьей прямой.
Для этого решим системы уравнений
2x + y −3 = 0,2x − y −1 = 0,
2x + y −5 = 0,2x − y −1 = 0,
Поскольку середина отрезка искомой прямой между параллельными прямыми лежит на прямой AB , то из равенства треугольников ACN и BDN следует, что точка пересечения N делит прямую AB пополам. Найдем ее координаты
xN = xA +2 xB = 54 , yN = yA +2 yB = 32 .
Рис. 3.25
114
Подставляя |
координаты |
точек |
M |
|
и |
|
N |
уравнение |
||||||||
прямой, проходящей через две точки, получим |
|
|
|
|||||||||||||
|
y − |
3 |
|
x − |
5 |
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
= |
|
4 |
, 8x +34 y −61 = 0. |
|
||||||||
5 |
− |
3 |
−3 − |
5 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
||
4.10. Даны уравнения двух |
сторон |
параллелограмма |
||||||||||||||
2x + y +9 = 0 и x − y − |
3 = 0 и точка |
M |
|
− |
7 |
, |
7 |
|
пересечения |
|||||||
|
|
|
|
|||||||||||||
2 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
его диагоналей. Составить уравнения двух других сторон параллелограмма.
Решение. Поскольку заданные стороны параллелограмма не параллельны, то найдем точку A их пересечения (рис. 3.26)
|
|
|
|
|
|
Рис. 3.26 |
|
|
|
|
|
|
||
|
|
|
|
2x + y + |
9 = 0, |
xA |
= −2, yA = −5. |
|
|
|||||
|
|
|
|
|
− y −3 = 0, |
|
|
|||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
||
|
Диагонали параллелограмма при пересечении делятся |
|||||||||||||
пополам. Отсюда координаты точки C |
|
|
|
|
|
|
||||||||
x |
= 2x |
− x |
A |
= −2 |
7 +2 |
= −5, y |
= 2 y |
M |
− y |
A |
= 2 |
7 |
+5 =12. |
|
C |
M |
|
|
2 |
|
C |
|
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Уравнения прямых BC и CD находим из уравнения пучка прямых проходящих через точку C . Прямая BC параллельна
115
AD , угловой |
коэффициент которой |
k = −2 , |
следовательно |
y −12 = 2(x +5), 2x + y −2 = 0. |
|
|
|
Прямая |
CD параллельна AB , |
угловой |
коэффициент |
которой k =1, |
y −12 = x +5, x − y +17 = 0. |
|
|
4.11. Даны две вершины треугольника A(5;1), B (1;3) и точка M (3; 4) пересечения его медиан. Составить уравнения
сторон треугольника.
Решение. Построим заданные точки (рис. 3.27). Медиана проходит через точку M и делит сторону AB пополам в точке D . Зная координаты точек A и B , находим координаты точки D
xD = xA +2 xB = 5 2+1 = 3, yD = yA +2 yB = 1+2 3 = 2.
Рис. 3.27 |
Рис. 3.28 |
Известно, что в треугольнике, точка пересечения медиан делит их в отношении 2 :1. Если обозначить за C
третью вершину треугольника, то будем иметь CMMD = 12 = λ .
Отсюда, по формулам деления отрезка в заданном отношении, имеем
xM = xC1++λλxD , yM = yC1++λλyD .
Откуда xC = (1+λ)xM −λxD = 3 3 −2 3 = 3, yC = (1+λ)yM −λyD = 3 4 −2 2 = 8 .
116
Итак, получили C (3;8). Используя уравнение прямой, проходящей через две точки, находим уравнения сторон
треугольника |
|
|
|
|
|
|
|
|||
AB : |
y −1 |
= |
x −5 |
, откуда x +2 y −7 = 0 , |
||||||
3 −1 |
|
|
|
|||||||
|
|
1−5 |
|
|
|
|||||
AC : |
y −8 |
= |
x −3 |
, откуда 7x +2 y −37 = 0, |
||||||
1−8 |
5 −3 |
|||||||||
|
|
|
|
|
|
|||||
BC : |
y −8 |
= |
x −3 |
, откуда 5x −2 y +1 = 0. |
||||||
3 −8 |
1−3 |
|||||||||
|
|
|
|
|
|
|||||
4.12. |
Даны уравнения x + y −8 = 0, x − y −2 = 0 двух |
|||||||||
медиан треугольника и |
координаты одной из его вершин |
|||||||||
A(4;6). Найти уравнения сторон треугольника. |
||||||||||
Решение. Координаты точки A(4;6) не удовлетворяют |
||||||||||
заданным уравнениям, |
следовательно, |
точка A не лежит на |
||||||||
медианах. |
|
|
|
|
|
|
|
|
|
|
Решая систему заданных уравнений, находим |
||||||||||
координаты точки M пересечения медиан xM = 5, yM = 3. |
||||||||||
Проведем две медианы, отметим точку М их |
||||||||||
пересечения и точку A (рис. 3.28). |
вершины B (xB , yB ) |
|||||||||
Пусть, например, |
координаты |
|||||||||
удовлетворяют первому уравнению, т. е. медиана проходит
через вершину треугольника |
B , а координаты вершины C |
|
удовлетворяют |
второму из |
заданных уравнений. Тогда |
xB + yB −8 = 0, xC − yC −2 = 0. |
|
|
Имеем |
два уравнения |
с четырьмя неизвестными. |
Составим еще два уравнения с теми же неизвестными. Медиана, проведенная через вершину A ,пройдет через точку
M и разделит сторону |
BC |
пополам в точке D . Найдем |
|||||||
координаты точки |
D : |
|
AM |
= 2 |
= λ, |
||||
|
|
|
|
|
MD |
1 |
|
|
|
x = |
xA +2xD |
, |
y |
M |
= |
yA +2 yD |
, |
||
|
|
||||||||
M |
1+2 |
|
|
|
|
1+2 |
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
117 |
|
|

xD = |
2xM −2xA |
= 3 5 −4 = 11 |
, |
||||||
|
|||||||||
|
2 |
|
|
|
|
2 |
|
2 |
|
yD = |
3yM − yA |
= |
3 3 −6 = |
3 . |
|
||||
2 |
|
||||||||
|
|
|
|
2 |
|
2 |
|
||
|
|
|
|
11 |
; |
3 |
|
|
|
Итак, имеем D |
2 |
2 |
. |
|
|
||||
|
|
|
|
|
|
|
|
||
Точка D делит BC пополам, следовательно, xD = xB +2 xC , yD = yB +2 yC ,
откуда xB + xC −11 = 0, yB + yC −3 = 0.
Составим систему
|
|
|
x |
|
+ x |
=11, |
|||||
|
|
|
|
|
B |
|
C |
|
|
|
|
|
|
|
yB + yC = 3, |
|
|||||||
|
|
|
|
|
|
|
|
=8, |
|
||
|
|
|
xB + yB |
|
|||||||
|
|
|
x |
|
− y |
= 2 |
|
||||
|
|
|
|
|
C |
C |
|
|
|
|
|
и найдем ее определитель |
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|||||||
= |
|
|
0 |
|
0 |
1 |
1 |
|
|
= −2 |
|
|
|
|
1 |
|
0 |
1 |
0 |
|
|
|
|
|
|
|
0 |
1 |
0 |
−1 |
|
|
|
||
Составим определитель |
xB |
|
|
|
|
||||||
|
11 |
|
|
1 |
0 |
0 |
|
|
|
||
|
|
|
|
|
|
||||||
xB = |
3 |
|
|
0 |
1 |
1 |
|
|
= −14. |
||
|
8 |
|
|
0 |
1 |
0 |
|
|
|
||
|
2 |
1 0 −1 |
|
||||||||
Находим xB = |
|
|
xB |
|
= −14 |
= 7. Подставляя xB в первое из |
|||||
|
|
|
|
|
|
|
−2 |
|
|
|
|
уравнений системы, находим xC = 4. Из остальных уравнений находим, что yB =1, yC = 2 .
118
Зная координаты точек B (7;1) и C (4; 2), находим уравнения сторон треугольника
AB : |
y −6 |
= |
|
|
x −4 |
|
, откуда 5x +3y −38 = 0 , |
|||
1−6 |
7 −4 |
|||||||||
|
|
|
|
|
||||||
AC : |
y −6 |
|
= |
x −4 |
|
, откуда x = 4, |
||||
2 −6 |
4 −4 |
|
||||||||
|
|
|
|
|
|
|||||
BC : |
y −1 |
= |
x −7 |
|
, откуда x +3y −10 = 0. |
|||||
2 −1 |
|
4 −7 |
|
|||||||
|
|
|
|
|||||||
4.13. |
Даны вершины A(−3; −2), B (4; −1) и C (1;3) |
|||||||||
трапеции ABCD (AB & BC ). Известно, что диагонали трапеции
взаимно перпендикулярны.
Найти координаты вершины D .
Решение. Прямая BC & AD , следовательно, их угловые коэффициенты равны. Воспользуемся уравнением прямой,
проходящей через две точки. Отсюда уравнение прямой |
BC |
||||||||||
примет вид |
|
|
|
|
|
|
|
|
|
|
|
|
y +1 |
= |
x −4 |
, 3y +4x = |
13, y = − 4 x +13 |
, |
k = − 4 . |
|
|||
|
3 +1 |
|
1−4 |
|
|||||||
|
|
|
3 |
3 |
|
3 |
|
||||
Для |
записи |
уравнения |
прямой |
AD |
воспользуемся |
||||||
уравнением |
пучка |
прямых, проходящих |
через |
точку |
A и |
||||||
условием параллельности BC & AD
y − yA = k (x − xA), y +2 = (x +3), 4x +3y +18 = 0.
Координаты точек A и C известны. Из уравнения прямой, проходящей через две точки находим, что уравнение прямой AC имеет вид
|
y +2 |
|
= |
x +3 |
, y = |
5 x + |
7 , k = |
5 . |
3 +2 |
|
|
||||||
|
1+3 |
|
4 |
4 |
4 |
|||
Из условия перпендикулярности диагоналей трапеции |
||||||||
находим угловой коэффициент диагонали BD : |
|
|||||||
|
k |
= − 1 , |
k = − 4 . |
|
|
|||
1 |
|
k |
1 |
5 |
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
119 |
|
|
|
Из уравнения пучка прямых, проходящих через точку B , находим уравнение прямой BD
y +1 = k1 (x − 4), y +1 = − 4 (x − 4), 4x +5y −11 = 0. |
||||||||
|
|
|
|
5 |
|
|
|
|
Решая уравнения прямых BD и AD совместно, |
||||||||
находим координаты точки D |
|
|
||||||
|
|
|
4x +5y −11 = 0, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
4x +3y +18 = 0. |
|
|
|||
2 y − 29 = 0, |
y = |
29 , |
4x + |
5 29 |
−11 |
= 0, |
x = −123 . |
|
|
||||||||
|
|
|
2 |
2 |
|
|
8 |
|
|
123 |
; |
29 |
|
|
|
||
Ответ: D − |
8 |
2 |
. |
|
|
|||
|
|
|
|
|
||||
3.5. Уравнение линии как геометрического места точек
Линии на плоскости соответствует уравнение с двумя переменными. Уравнение с двумя переменными, которому удовлетворяют координаты любой точки, лежащей на линии, называется уравнением данной линии.
Всякому уравнению первой степени с двумя неизвестными на плоскости соответствует прямая линия.
Кривыми второго порядка называются кривые, уравнения которых в прямоугольных координатах представляют уравнения второй степени с двумя неизвестными
Ax2 |
+ 2Bxy +Cy2 + 2Dx + 2Ey + F = 0. |
(1) |
|
Существуют три типа таких кривых: |
|
||
если AC − B2 |
> 0, кривая эллиптического типа, |
|
|
если AC − B2 < 0 – гиперболического типа, |
|
||
если AC − B2 |
< 0 - параболического типа. |
|
|
Если в общем уравнении второй степени (1) |
|||
коэффициенты |
при |
квадратах текущих координат |
равны |
|
|
120 |
|
