2582

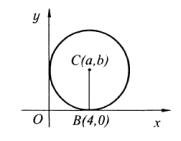
6.3. Составить уравнение окружности, проходящей через точку A(7;9) и касающейся оси Ox в точке B (4;0).

Решение. Делаем схематический чертеж (рис. 3.36).

проходит через центр окружности C (a,b). Уравнение искомой окружности примет вид (x −4)2 +(y − R)2 = R2 . Подставляя в

уравнение окружности примет вид (x −4)2 +(y −5)2 = 25 .

6.4. Не выполняя построения, установить, как расположены относительно окружности

x2 + y2 +8x −4 y −29 = 0

точки: A(4;3), B (−1; 2), C (−4,9).

Решение. Подставляя координаты точки A в уравнение

6.5. Составить уравнение эллипса, зная, что он проходит через точки M ( 3; −2) и N (−2 3;1) и его оси

симметрии совпадают с осями координат. Найти уравнения его директрис, координаты вершин и фокусов, вычислить эксцентриситет и величины фокальных радиусов точки M .

Решение. Уравнение эллипса имеет вид (2). Точки M и N принадлежат эллипсу, значит их координаты удовлетворяют его уравнению. Подставляя их в уравнение

эллипса, получим систему двух уравнений относительно a2 и b2

132

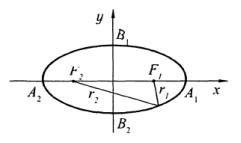
Рис. 3.37

6.6. Расстояния одного из фокусов эллипса до концов его большой оси, соответственно, равны 8 и 2. Составить каноническое уравнение эллипса.

Решение. Данные расстояния могут быть представлены

6.8. Оси эллипса совпадают с осями координат и равны: a =10 , b =1. Определить длину сопряженных полудиаметров a ' и b ' и направление диаметра 2b ' если известно, что

диаметр 2a ' образует с осью 2a угол 20D .

133

полудиаметра находим по формуле расстояния между двумя точками

Угловой коэффициент сопряженного диаметра находим по формуле (5)

6.9. Составить уравнение гиперболы, зная, что ее оси совпадают с осями координат и гипербола проходит через

точки M (5; −2) и N (3 2; 2 ). Найти уравнения директрис и

вычислить эксцентриситет гиперболы.

Решение. Координаты точки M и N должны удовлетворять каноническому уравнению гиперболы (6). Подставляя их в уравнение гиперболы получим систему уравнений

25a2 − b42 =1, 18a2 − b22 =1.

134

ее координаты и значения a и b каноническое уравнение (6),

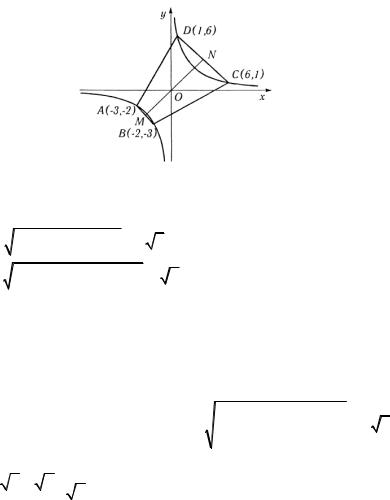
Решение. Строим чертеж (рис. 3.38) и определяем координаты вершин трапеции. Система уравнений xy = 6 ,

x + y +5 = 0 дает значения координат точек A(−3; −2); B (−2; −3). Вторая система xy = 6 , x + y −7 = 0 дает значения координат точек C (6;1) и D (1;6),

Рис. 3.38

представляет отрезок MN биссектрисы координатного угла, заключений между основаниями трапеции. Совместное

6.12. Преобразовать к простейшему виду уравнение y = 34xx +−53 и построить гиперболу, определяемому этим

уравнением.

Решение. Выполним преобразование заданного уравнения параллельным переносом осей по формулам x = x '+a , y = y '+b .

137

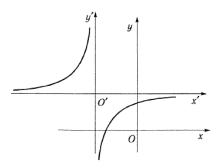
Рис. 3.39

6.13. Составить уравнение гиперболы, если известны точка пересечения ее асимптот O′(2; −3) и одна из вершин

A(4; −1).

Решение. Относительно системы координат с началом

вточке O′(2; −3) пересечения асимптот условию

y= −3xx−+210 .

6.14.Написать уравнение параболы, зная, что ось симметрии ее совпадает с осью Ox , а вершина—с началом координат и расстояние от вершины до фокуса равно 5.

138

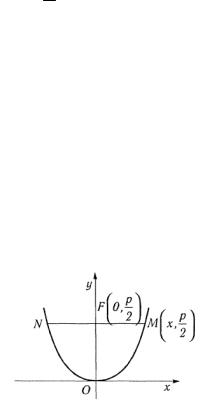
Решение. Каноническое уравнение параболы имеет вид

6.15. Составить уравнение параболы, если парабола симметрична относительно оси Oy , вершина совпадает с

началом координат, а фокус находится в точке F (0;3).

Решение. Поскольку парабола симметрична относительно оси Oy , то каноническое уравнение имеет вид

x2 = 2 py. По условию 2p = 3, p = 6.

Отсюда уравнение параболы x2 =12 y.

6.16. Для параболы x2 = 2 py. найти длину хорды, перпендикулярной к оси Oy и проходящей через фокус.

Рис. 3.40

139

6.17. Определить координаты вершины параболы, величину параметра и уравнение оси симметрии, если

парабола задана уравнением y2 −8x −4 y +12 = 0.

Решение. Дополним левую часть уравнения до полного квадрата переменной у

y2 −4 y +4 −8x +12 −4 = 0 или (y −2)2 = 2 4(x −1).

Следовательно, вершина параболы имеет координаты xb =1, yb = 2. Параметр p = 4 , а ось симметрии параллельна

оси Ox и имеет уравнение y = 2.

6.18. Найти уравнение параболы, симметричной относительно оси ординат, если известно, что парабола

проходит через точки M (−3;6) и N (2; −4).

Решение. Искомое уравнение параболы примем в виде

a = 2, c = −12. Следовательно, условиям задачи удовлетворяет парабола y = 2x2 −12.

6.19. Найти уравнение параболы, симметричной относительно оси ординат, если известно, что парабола проходит через точки (1;2), (2;4) и (3;8).

Решение. Подставляя координаты точек в общее уравнение параболы, получим систему

a +b +c = 2,4a +2b +c = 4,

9a +3b +c =8.

Из решения системы находим, что a =1, b = −1, c = 2. Таким образом, условиям задачи удовлетворяет парабола y = x2 − x +2.

6.20. Найти координаты вершины, написать уравнение оси симметрии и построить параболу, заданную уравнением y = 5 +4x − x2 .

140