
2582
.pdf
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
′2 |
|
|
|
|
|
2 |
|
|
|
|
|
′ ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
3x |
|
|
− |
6 y +3y |
|
−2x −8y + |
4 |
|
= 3x |
|
|
|
cos |
|
|
α −6x y |
cosα sinα + |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
+3y |
′2 |
|
sin |
2 |
−6(x |
′2 |
|
|
|
|
|
|
|
|
|
|
|
′ ′ |
cos |
2 |
|
|
|
|
′ ′ |
sin |
2 |
α − y |
′2 |
cos |
2 |
α sinα)+ |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
cosα sinα + x y |
|
α − x y |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
+3x |
′2 |
sin |
2 |
|
|
|
|
|
|
′ |
′ |
cosα sinα +3y |
′2 |
cos |
2 |
|
|
|
|
|
′ |
cosα |
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
α +6x y |
|
|
|
|
α −2x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
′ |
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosα |
+ 4 |
|
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
+2 y |
sinα −8x |
|
sinα −8y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Подберем |
угол |
|
|
|
|
|
так, |
|
|
|
|
чтобы |
|
|
|
|
коэффициент |
|
при |
|||||||||||||||||||||||||||||||||||||||
′ |
|
|
′ |
обратился |
|
в |
нуль: |
|
|
|
|
cos |
2 |
α |
−sin |
2 |
α = 0 , |
|
откуда |
α = |
π |
|||||||||||||||||||||||||||||||||||||||||||
x , y |
|
|
|
|
|
|
|
|
|
|
4 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Уравнение кривой в этом случае примет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3y′2 |
|
(sin2 α +2sinα cosα +cos2 α) |
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
−2x |
′ |
|
|
|
|
|
+2 y |
′ |
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
|
|
|
|
|
′ |
|
|
|
|
|
23 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
cosα |
sin |
α |
− |
|
|
|
sinα − |
|
|
|
|
cosα + 4 |
|
= 0 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
8x |
|
8y |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
Или |
|
6 y′ |
2 |
−6 y′ |
|
2 |
−5 |
2x′+ |
23 |
= 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
Дальнейшее |
упрощение |
|
|
|
уравнения проводится |
при |
||||||||||||||||||||||||||||||||||||||||||||||||||||
помощи параллельного перенесения осей Ox |
′ |
|
|
|
|
|
′ |
|
Выделим |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
иOy . |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
полный |
|
|
квадрат |
6 y′− |
|
|
|
|
|
= 5 |
|
|
2 x′− |
|
|
|
|
|
|
. |
|
Введем |
|
|
новые |
|||||||||||||||||||||||||||||||||||||||
|
|
8 |
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x′ = |
x′′+ |
|
|
2 |
, y′ = y′′ |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
координаты |
|
|
|
|
|
|
|
+ 8 |
, |
|
|
|
|
|
|
что |
|
|
|
соответствует |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
параллельному перемещению осей на величину |
|
|
|
|
2 |
|
по оси |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ox |
′ |
|
|
|
и |
|
|
на |
|
|
|
величину |
|
|
|
|
по |
|
|
|
|
оси |
|
|
|
Oy |
′ |
. |
В |
|
координатах |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
′′ |
|
|
|
′′ |
уравнение |
|
|
кривой |
|
примет |
|
вид |
|
|
|
y |
′′2 |
= |
5 |
2 |
|
x |
′′ |
- |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
x , y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
каноническое уравнение параболы. Ветви параболы расположены симметрично относительно оси x′′и совпадают с положительным направлением этой оси (рис. 3.53).
151
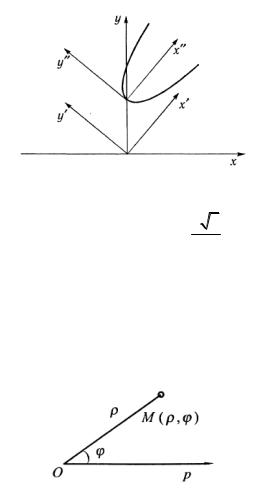
Рис. 3.53
Вершина параболы находится в начале координат
системы x′′, y′′; параметр параболы p = 5122
3.8. Полярная система координат. Уравнения кривых
1°. Полярными координатами точки М (рис. 3. 54) являются полярный радиус ρ и полярный угол ϕ , для
которых приняты |
следующие интервалы изменения |
ρ [0, ∞[иϕ [0, 2π[ |
или ϕ [−π,π[. |
Рис. 3.54
Если начала координат прямоугольной и полярной системы совпадают, а полярная ось совмещена с положительным направлением оси Ox , то прямоугольные координаты точки М выражаются через полярные по формулам
x = ρ cosϕ, y = ρsinϕ. |
(1) |
152

Полярные |
координаты |
выражаются |
через |
||||||
прямоугольные по формулам |
|
|
y |
|
|
|
|||
ρ = |
x2 + y2 , |
ϕ = arctg |
. |
|
(2) |
||||
|
|||||||||
|
|
|
|
|
x |
|
|||
Вторую из формул (2) иногда удобнее заменить двумя |
|||||||||
следующими формулами |
|
|
|
|
|
|
|||
sinϕ = |
y |
cosϕ = |
|
|
x |
|
|||
|
|
|
|
. |
(3) |
||||
x2 + y2 |
|
x2 + y2 |
|||||||
Проекции произвольного отрезка на координатные оси
выражаются через его длину и полярный угол формулами: |
|
x2 − x1 = d cosϕ, y2 − y1 = d sinϕ. |
(4) |
Полярный угол отрезка по координатам его конца и начала определяется по формуле
tgϕ = y2 − y1 . x2 − x1
2°. Если за полюс принять один из фокусов линии второго порядка (рис. 3.55), то уравнение линии в полярной
системе координат примет вид |
|
|||||
|
|
ρ = |
|
p |
|
|
|
|
|
. |
(5) |
||
1−ε cosϕ |
||||||
где ε = |
ρ |
- эксцентриситет, |
d - расстояние точки M (ρ,ϕ) до |
|||
|
||||||
|
d |
|
|
|
||
дирекртис, ρ - параметр |
линии второго |
порядка, равный |
||||
половине длины хорды, проходящей через фокус и перпендикулярной фокальной оси.
Рис. 3.55
153

Если ε = 0 , то уравнению (5) соответствует окружность, если ε <1 - эллипс, если ε >1 - гипербола, если ε =1 - парабола.
Если полярную ось ориентировать в противоположную сторону, то уравнение линии второго порядка в полярной
системекоординат имеет вид |
p |
|
|
ρ = |
(6) |
||
1+ε cosϕ |
3°. Рассмотрим некоторые линии, уравнения которых заданы в полярной системе координат.
1. ϕ = a (а - радиан) - геометрическое место точек,
полярный угол которых имеет постоянныю величину, есть луч, выходящий из полюса полярной системы координат (рис. 3.56).
Рис. 3.56
2. ρ = a - окружность с центром в полюсе и с радиусом,
равным а.
3. ρ = 2a cosϕ - окружность, центр которой находится на полярной оси в точке C (a, 0) и радиус которой равен а
(рис. 3.57).
Рис. 3.57
154
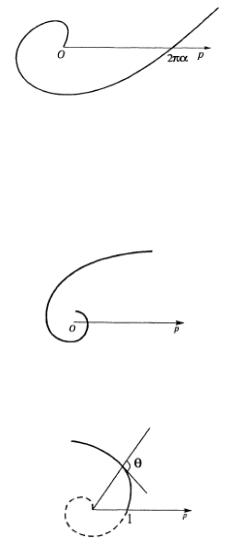
4. ρ = aϕ (a −const ) - спираль Архимеда (рис. 3.58).
|
a |
|
Рис. 3.58 |
|
5. ρ = |
(const ) - |
гиперболическая спираль ϕ ≠ 0 |
||
|
||||
ϕ |
|
|
||
(рис. 3.59). Здесь ρ ≠ 0 |
и полюс называют поэтому |
|||
асимптотической точкой кривой, т. е. такой точкой, к которой точки кривой неограничено приближаются, но никогда ее не достигают.
Рис. 3.59
6. ρ = aϕ (a > 0) - логарифмическая спираль (рис. 3.60)
Рис. 3.60
Логарифмическая спираль с любой прямой, проведенной через полюс образует один и тот же угол θ .
155
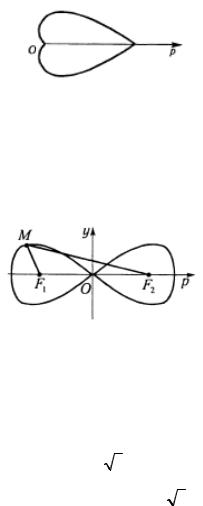
Изменению ϕ от 0 до −∞ соответствует часть графика спирали, которая изображена пунктиром (рис. 3.60).
7. ρ = 2a (1+cosϕ) - кардиоида (рис. 3.61). Это
траектория, которую опишет точка окружности, катящееся без скольжения по окружности равного радиуса, касаясь ее внешним образом.
Рис. 3.61 |
|
|
|
|
|
|||||
8. Лемниската Бернулли |
ρ2 = 2a2 cos 2ϕ (рис. 3.62). |
|||||||||
Характеристическое свойство |
|
|
F M |
|
|
|
F M |
|
= a2 |
−const , где |
|
|
|
|
|||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
F1 (−a;0), F2 (a;0).
|
|
|
|
|
|
|
|
Рис. 3.62 |
|
|
|
||
|
|
8.1. |
Найти |
декартовы |
координаты |
точек |
|||||||
|
|
2π |
|
|
π |
|
|
|
|
|
|
|
|
A |
2; |
|
|
, B 3; − |
. |
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Решение. |
Применяя |
формулы |
(1), |
находим |
|||||||
xA |
= 2cos |
2π |
= −1, |
yA |
= 2sin |
2π |
= |
3. |
|
|
|
||
3 |
|
|
|
|
|||||||||
|
|
|
|
|
|
3 |
|
|
|
3). |
|
||
|
|
В декартовой системе получим A(1; |
|
||||||||||
|
|
|
|
|
|
|
156 |
|
|
|
|
||
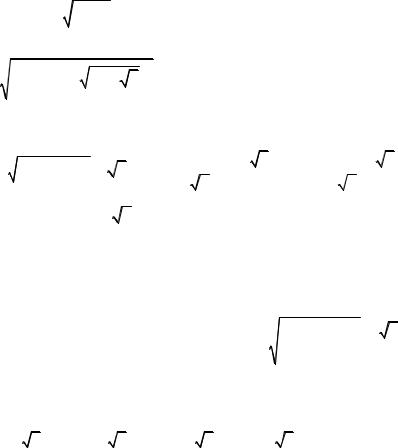
Декартовы |
координаты |
|
|
точки |
В |
будут: |
||||||
|
− |
π |
|
|
|
− |
π |
|
|
|
|
−3). |
xB = 3cos |
2 |
= 0, |
yB = 3sin |
2 |
= −3, то есть B (0; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
8.2. |
|
|
Найти |
полярные |
|
координаты |
точек |
|||||
A(−2;0), B (1; −1). |
|
|
|
|
|
|
|
|
|
|||
Решение. Применяя формулы (2), (3), находим |
||||||||||||
координаты точки А |
|
|
|
|
|
0 |
= 0, cosϕA = −2 |
|
||||
ρA = |
(−2)2 |
+02 |
= 2, sinϕA |
= |
= −1. |
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
По численным значениям синуса и косинуса находим, что
d = |
(4 −3)2 +( |
3 −2 |
3 )2 |
= 2. ϕA =π . |
Таким |
образом, |
|
в |
||||||||||||
полярной системе |
A(2;π ). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Полярные |
|
|
координаты |
точки |
B |
|
будут |
|||||||||||
ρB = |
|
(1)2 +(−1)2 |
= |
2, sinϕB = |
−1 −1 |
= − |
2 |
, cosϕB |
= |
1 |
= |
|
2 |
, |
||||||
|
2 |
|
2 |
2 |
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ϕB = − |
π |
, то есть |
B |
|
2; − |
π |
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
8.3. Найти полярные координаты вершин квадрата со стороной а, равной единице, изображенного на рис. 3.63.
Решение. AB = BC = CD = DA =1. Полярные радиусы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
1 2 |
2 |
|
||
всех |
вершин |
квадрата |
|
равны |
|
|
ρ = |
|
|
|
|
+ |
= |
|
. |
|||||||||||
|
|
|
|
|
2 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|||
Полярные |
|
|
|
углы: |
|
|
ϕC = |
π |
, ϕD = 3π |
, ϕA = |
5π |
, ϕB = |
7π . |
|||||||||||||
Следовательно: |
|
|
|
|
|
4 |
|
|
|
|
4 |
|
|
|
|
|
4 |
|
4 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
5π |
|
2 |
|
7π |
|
|
|
2 |
|
π |
|
|
|
2 |
|
3π |
|
|
|
|
|||
A |
|
; |
|
|
, B |
|
; |
|
|
, C |
|
|
; |
|
|
, D |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
2 4 |
|
|
2 4 |
|
|
2 4 |
|
|
|
2 4 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
157 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
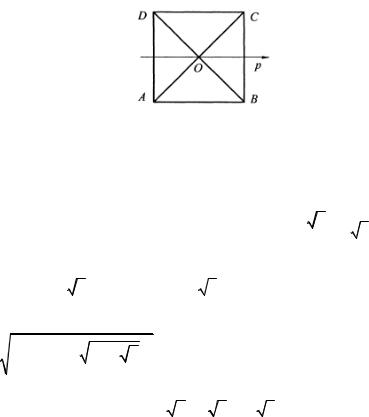
Рис. 3.63
8.4. Найти проекции отрезка на координатные оси, зная его длину d = 6 и полярный угол ϕ =120D.
Решение. По формулам (4) находим
X = 6cos120D = 6 |
|
− |
1 |
|
= −3, Y = 6sin120D = 6 |
3 |
= 3 3. |
|
|
|
|
|
|||||
2 |
2 |
|||||||
|
|
|
|
|
|
8.5. Найти полярный угол отрезка, направленного из |
|||||||||
точки M1 (3;2 3) |
в точку M2 (4; 3). |
|
|
|
|||||
Решение. |
Длина |
отрезка |
|
M1M2 |
равна |
||||
d = (4 −3)2 +( 3 −2 3 )2 |
= 2. |
|
|
|
|
||||
Применяя формулы (4), находим: |
|
|
|
||||||
cosϕ = |
4 −3 = |
1 , sinϕ |
= |
|
3 −2 3 |
= − |
3 |
. Отсюда следует, |
|
|
2 |
2 |
|||||||
|
2 |
2 |
|
|
|
|
|
||
что главное значение ϕ = 300D. |
|
|
|
||||||
8.6. Даны точки M1 (1;0) и M2 (3;5). Найти проекцию |
|||||||||
отрезка |
M1M2 |
на ось, |
проходящую через |
точки |
|||||
A(-1;2) и B(3;5) и направленную от А к В. |
|
||||||||
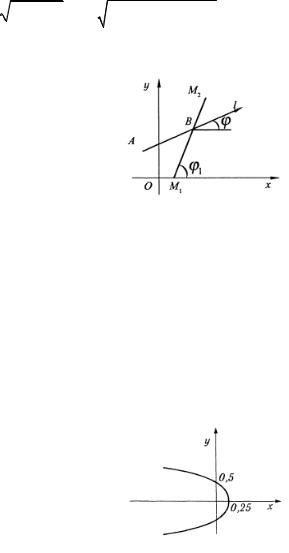
Решение. Обозначим через l данную ось (рис. 3.64), |
|||||||||
через ϕиϕ1 - полярные углы отрезков AB иM1M2 . Из простых |
|||||||||
геометрических |
соображений |
находим, |
что |
||||||
Пр.l M1M2 |
= M1M2 cos (ϕ1 −ϕ)= M1M2 (cosϕ1 cosϕ +sinϕ1 sinϕ). |
||||||||
Отсюда, пользуясь формулами (4) и обозначая через X , Y - проекции на координатные оси отрезка AB , а через
158
X1Y1 |
- |
проекции |
отрезка |
M1M2 , |
|
получим: |
||||||||||||
|
|
= M1M2 cos (ϕ1 −ϕ) |
|
|
|
X1 |
|
X |
|
|
Y1 |
|
Y |
|
|
X1 X +Y1 |
||
Пр.l |
M1M2 |
= M1M2 |
|
+ |
|
|
|
= |
||||||||||
|
|
|
|
|
d |
|||||||||||||
|
|
|
|
|
|
|
|
M1M2 d |
M1M2 d |
|
||||||||
где |
d |
- |
длина |
|
|
отрезка |
|
AB , |
|
равная |
||||||||
d = X 2 +Y 2 = = (3 +1)2 +(5 −2)2 = 5. |
|
|
|
|
|
|
|
|
|
|
||||||||
|
Таким образом, Пр. |
M |
M |
2 |
= (3 −1)4 +(5 −0)3 = 23 . |
|
|
|||||||||||
|
|
|
l |
1 |
|
|
5 |
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Рис. 3.64 |
1 |
|
|
8.7. |
|
|
|
||
Линия |
задана уравнением |
ρ = |
|
. |
|
2 +2cosϕ |
|||||
Требуется: а) построить линию по точкам, |
начиная от ϕ = 0 |
||||
до ϕ = 2π , |
придавая |
ϕ значения через |
промежуток π ; |
||
|
|
|
4 |
|
|
б) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью; в) по полученному уравнению определить, какая это линия.
Решение. а) Составим таблицу и строим линию по точкам
(рис. 3.65)
Рис. 3.65 159
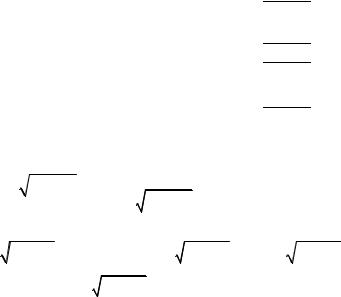
|
ϕ |
|
0 |
|
π |
|
π |
|
π |
π |
5π |
3π |
7π |
|
2π |
|||||
|
|
|
|
|
|
|
4 |
|
2 |
3 |
|
4 |
|
4 |
|
4 |
|
|
||
|
cosϕ |
|
1 |
|
0,707 |
0 |
-0,707 |
-1 |
-0,707 |
0 |
0,707 |
|
1 |
|||||||
1 |
|
|
0,25 |
0,29 |
0,5 |
1,7 |
∞ |
1,7 |
|
0,5 |
|
0,29 |
|
0,25 |
||||||
|
2 +2cosϕ |
|
|
|
|
|
||||||||||||||
|
б) Между декартовыми и полярными координатами |
|||||||||||||||||||
существует |
|
|
зависимость |
|
y = ρsinϕ, x = ρ cosϕ, |
откуда |
||||||||||||||
|
ρ = x2 + y2 , cosϕ = |
|
|
x |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
x2 + y2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Подставляя эти значения в данное уравнение, получим |
|||||||||||||||||||
2 x2 + y2 = |
|
|
|
1 |
|
|
, 2( |
x2 + y2 + x)=1, |
x2 + y2 = 1−2x |
, |
||||||||||
|
|
|
1 |
|
|
|||||||||||||||
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||
|
|
|
|
|
x2 + y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
4x2 +4 y2 =1−4x +4x2 , 4x =1−4 y2 , x = 14 − y2 .
в) Полученное уравнение x = 14 − y2 - есть уравнение параболы.
3.9. Параметрические уравнения плоских кривых
Уравнения x =ϕ(t ), y =ψ (t ), где t - параметр,
называются параметрическими уравнениями кривой. Для того чтобы получить уравнение кривой в прямоугольных координатах, из двух параметрических уравнений нужно исключить параметр.
1.Параметрические уравнения окружности:
x= a cos t, y = a sin t, t [0, 2π].
2.Параметрические уравнения эллипса:
x= a cos t, y = b sin t, t [0, 2π].
160
