2582

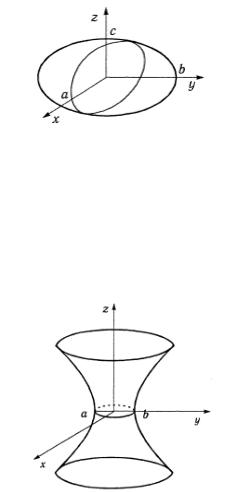
Рис. 4.4

2°. Однополостный гиперболоид. Каноническое

где a,b — полуоси эллипса в плоскости xOy (рис. 4.5).

Рис. 4.5

Форму поверхности определяют методом сечений. При

всех возможных эллипсов, который называется горловым.

181

точку однопостного гиперболоида проходят две прямые,

и поверхность, соответствующая этому уравнению, называется

однополостным гиперболоидом вращения. Она образуется вращением гиперболы вокруг ее мнимой оси.

3°. Двухполоетный гиперболоид. Каноническое уравнение имеет вид

вершины поверхности (рис. 4.6). В сечении с плоскостями

Поверхность (5) симметрична относительно плоскости yOz . 182

Рис. 4.6

При b = c уравнение (5) принимает вид

и поверхность, соответствующая этому уравнению, называется

двухполостным гиперболоидом вращения. Она образуется при вращении гиперболы вокруг оси Ox .

Рис. 4.7

183

В сечении с плоскостями xOz и yOz поверхность

соответствующая этому уравнению, называется параболоидом вращения. Она образуется вращением параболы вокруг оси z.

5°. Гиперболический параболоид. Каноническое уравнение имеет вид

которых действительная ось параллельна оси Ox . Сечения с плоскостями z = h - гиперболы, у которых действительная ось параллельна оси Oy . Сечения поверхности с плоскостями xOz и yOz представляют параболы x2 = 2 pz и y2 = −2 pz.

Рис. 4.8

184

осям координат.

6°. Цилиндрические поверхности. Уравнения, не содержащие какой-либо одной координаты, в пространстве изображаются цилиндрическими поверхностями, образующие которых параллельны отсутствующей координатной оси. Само же уравнение есть уравнение направляющей кривой этого цилиндра.

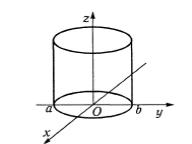
1. Эллиптический цилиндр (рис. 4.9)

эллипс.

Если a = b , то направляющая есть круг, а цилиндр называется круговым.

Рис. 4.9

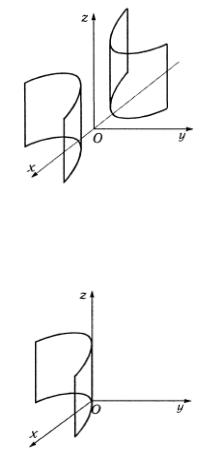
2. Гиперболический цилиндр (рис. 4.10)

185

Направляющей является гипербола.

Рис. 4.11

Направляющей является парабола.

Аналогично записываются уравнения цилиндрических поверхностей с образующими, параллельными координатным осям Ox и Oy.

186

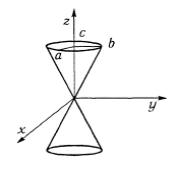
7°. Поверхность, образованная движением прямой, проходящей через неподвижную точку пространства и пересекающей при этом некоторую кривую, называется

конической поверхностью.

Неподвижная точка называется вершиной, кривая —

направляющей и прямая - образующей конической поверхности.

Каноническое уравнение конуса, когда ось симметрии конуса совпадает с осью Oz (рис. 4.12), имеет вид

Рис. 4.12

5.1. По заданному уравнению f (x, y, z)= 0 определить

вид поверхности и указать ее расположение в координатной системе:

а) x2 + y2 + z2 −2x +4 y −6z +5 = 0; б) 4x2 +4 y2 +5z2 −20 = 0;

в) 5x2 +5y2 −4z2 −20 = 0; г) 4x2 + y2 −2z = 0; д) x2 + z2 − y = 0;

ж) y2 −4z −5 = 0; з) y2 −8x +3 = 0. 187

z = x2 + y2 . 1 2

2

Данное уравнение представляет эллиптический параболоид (5).

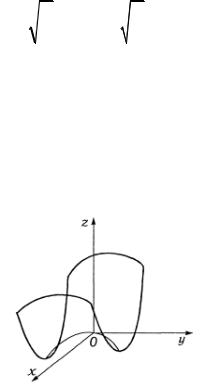
д) Разрешим выражение относительно у, тогда получим y = x2 + z2 .Нетрудно заметить, что это уравнение предствляет параболоид вращения с осью вращения у (рис. 4.13).

188

Рис. 4.13

ж) Поскольку переменная x отсутствует, то уравнение z = 14 y2 − 54 представляет параболический цилиндр с

образующими параллельными оси x (рис. 4.14). Сечение параболического цилиндра с плоскостью Oyz образует

параболу, вершина которой находится в точке с координатой z = − 54 .

образующие которого параллельны оси z (рис. 4.15). Сечение параболического цилиндра с плоскостью Oxy образуют

189

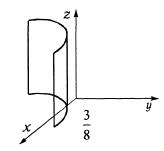
параболу, вершина которой находится в точке с координатой x = 83 .

Рис. 4.15

5.2. Установить поверхность, определяемую уравнением:

а) 4x2 +9 y2 +16z2 −16x +36 y +32z +59 = 0; б) x2 −4 y2 +4z2 +2x +8y −7 = 0 ;

в) x2 −16 y2 −4z2 −10x −64 y +24z −48 = 0 ; г) 5x2 +2 y +3z2 −9 = 0 .

Решение. а) Поскольку уравнение не содержит произведений координат, то приведение его к простейшему виду осуществляется посредством параллельного переноса. Вьщелим полные квадраты

4x2 +9x2 +16x +36 y +32z +59 =

=4(x2 −4x +4)+9(y2 + 4 y + 4)+16(z2 + 2z +1)−9 =

=4(x −2)2 +9(y +2)2 +16(z +1)2 −9

x, y, z паралельным переносом начала в точку с координатами a = 2, b = −2, c = −1 данная поверхность имеет простейшее уравнение вида

190