
2582
.pdf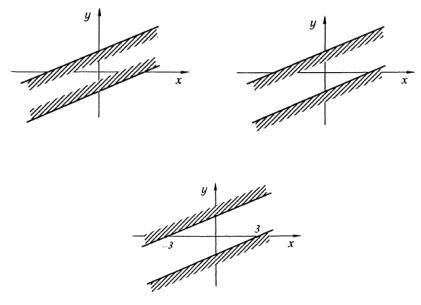
включается в искомую область; б) при одинаковых знаках в системе общая часть совпадает с полуплоскостью, которая не включает другой граничной прямой, то есть геометрическим изображением служит полуплоскость х−2 у−3 > 0 (рис. 3.14);
в) в данном случае полуплоскости не имеют никакого пересечения, то есть общей области вовсе не существует (рис. 3.15).
Рис. 3.13 |
Рис. 3.14 |
Рис.3.15
3.10. Построить область, координаты точек которой
удовлетворяют системе неравенств у > 2x +4, |
х > −5, |
x |
+ |
y |
≤1. |
||
|
3 |
||||||
|
|
|
5 |
|
|
||
Решение. На плоскости Оху строим сначала прямую |
|||||||
y = 2x +4 . Для этого |
полагаем |
х = 0, у = 0, |
находим |
точки |
|||
пересечения прямой |
с осями |
координат |
y = 4, 4 < x = −2 и |
||||
проводим через эти точки прямую (рис. 3.16). Неравенство у > 2x +4 будет представлять область, координаты точек
которой расположены выше построенной прямой, причем сама
101
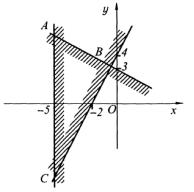
прямая в искомую область не включается. Неравенство x > −5 представляет область расположенную правее прямой x = −5 . Последнее неравенство напоминает уравнение прямой в отрезках на осях.
Рис. 3. 16
Откладывая по осям Ох, Оу точки а = 5 и b = 3 и проводя через них прямую, находим, что область удовлетворяющая этому неравенству расположена ниже прямой. Из построений видно, что искомая область представляет треугольник ABC, где отрезок АВ принадлежит области.
3.11. Найти область, координаты точек которой удовлетворяют системе неравенств:
2x − y +4 > 0, |
3х− у+4 ≥ 0, |
|
|
||
a) |
x < 0; |
б) x + y −2 ≥ 0, |
|
x −2 y −6 > 0. |
|
|
|
|
Решение. а) Поскольку из первого неравенства при х=0, y = 0 4 > 0, то полуплоскость включает начало координат
(рис. 3.17).
102

Рис. 3.17
Неравенству х < 0 соответствуют все точки левой полуплоскости. Решением является общая часть или
пересечение |
этих полуплоскостей, ограниченная прямыми |
2x − y +4 = 0, |
х = 0 пересекающимися под углом α . |
б) При х = 0, у = 0 из первого неравенства следует, что полуплоскость включает начало координат (рис. 3.18); из второго - следует, что полуплоскость не включает начало координат; из третьего, что не включает. Следовательно, имеются лишь три изолированных пересечения двух полуплоскостей, обозначаемых, соответственно, углами α, β,γ между прямыми
3x − y +4 = 0, х+ у−2 = 0 и х−2 у−6 = 0
Рис.3.18
103
3.4. Задачи на прямую линию
1°. Точка пересечения двух прямых. Пусть прямые заданы уравнениями
|
|
Ах+ В у+С = 0; A x + B y +C |
2 |
= 0 . |
|
|
(1) |
|||||||||||||||||
|
|
1 |
1 |
|
1 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
||||
Координаты точки пересечения находятся из решения |
||||||||||||||||||||||||
этой системы |
|
|
C |
B −C B |
|
|
|
A C − AC |
|
|
|
|
|
|
||||||||||
|
|
x = |
|
|
y = |
2 |
|
|
|
|
|
|||||||||||||
|
|
|
2 |
2 |
1 |
2 |
; |
|
2 |
1 |
1 |
|
. |
|
|
(2) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
A B − A B |
|
|
|
A B − A B |
|
|
||||||||||||||
|
|
|
1 |
2 |
2 |
1 |
|
|
|
|
|
1 |
2 |
|
2 |
|
1 |
|
|
|
|
|
||
При этом возможны следующие случаи: |
|
|
||||||||||||||||||||||
a) A B − A B ≠ 0 или |
А1 |
|
≠ |
В1 |
|
- прямые пересекаются в |
||||||||||||||||||
|
|
|
||||||||||||||||||||||
1 |
2 |
2 |
1 |
|
|
А2 |
|
В2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
определенной точке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
А1 |
|
В1 |
≠ С1 |
|
||||||||
б) A B − A B = 0 и С В −С В ≠ 0 или |
= |
- |
||||||||||||||||||||||
|
|
|||||||||||||||||||||||
1 |
2 |
2 |
1 |
|
2 |
1 |
|
|
1 |
2 |
|
|
|
|
А2 В2 |
С2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
прямые параллельны, точек пересечения нет.
в) A B − A B = 0 и С В −С В = 0 или |
А1 |
= |
В1 |
= |
С1 |
- |
|||||||
|
|
|
|||||||||||
1 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
А2 |
|
В2 |
|
С2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
обе прямые сливаются в одну, система уравнений сводится к одному уравнению, точек пересечения бесчисленное множество.
2°. Под углом между двумя прямыми (рис. 3.19)
(L1 ) y = k1x +b1; (L2 ) y = k2 x +b2 , |
(3) |
понимают угол ϕ , отсчитываемый от прямой L1 против часовой стрелки, до прямой L2
tgϕ = |
k2 −k1 |
(4) |
|
|
|||
|
1+k k |
2 |
|
|
1 |
|
|
104
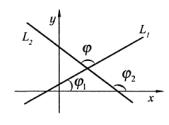
Рис. 3.19
Если прямые заданы общими уравнениями (1), то формула (4) принимает вид
tgϕ = |
A1B2 − A2 B1 |
. |
|
|
(5) |
||||||||||
A A + B B |
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
1 |
2 |
|
1 |
2 |
|
|
|
|
|
|
Условие параллельности прямых |
|
|
|||||||||||||
k |
|
= k |
2 |
или |
|
|
А1 |
|
= |
В1 |
. |
(6) |
|||
|
|
|
|
||||||||||||
1 |
|
|
|
|
|
|
|
А2 |
|
В2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Условие перпендикулярности прямых |
|
||||||||||||||
k = − |
1 |
|
|
или |
A A + B B = 0. |
(7) |
|||||||||
|
|
||||||||||||||
1 |
|
k2 |
|
|
|
|
1 |
2 |
|
1 |
2 |
|
|||
3°. Уравнение |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пучка |
|
прямых. |
Пучком |
прямых, |
|||||||||||
проходящих через данную точку M (x0 , y0 ), называют совокупность всех прямых, проходящих через эту точку
y − y0 = k (x − x0 ). |
(8) |
Точка M (x0 , y0 ) называется центром пучка. Угловой
коэффициент k в уравнении пучка прямых неопределен. Уравнение пучка прямых, проходящих через точку
пересечения двух данных прямых (1), имеет вид
A1x + B1 y +C1 +λ(A2 x + B2 y +C2 )= 0. |
(9) |
Здесь параметр λ неопределен. |
|
4°. Расстояние от данной точки до данной |
прямой. |
Чтобы найти расстояние от точки M1 (x1, y1 ) до прямой, нужно в левую часть нормального уравнения прямой вместо текущих
105
координат подставить координаты точки M1 и взять абсолютную величину получившегося числа
d = |
|
x1 cosα + y1 sinα − p |
|
. |
(10) |
|
|
Если прямая задана общим уравнением, то формула (10) принимает вид
|
|
d = |
Ax1 + By1 +C |
|
. |
|
(11) |
|||||||||
|
|
A2 + B2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
5°. Уравнения биссектрис углов между прямыми (1) |
||||||||||||||||
|
A1x + B1 y +C1 |
= ± |
A2 x + B2 y +C2 |
. |
(12) |
|||||||||||
|
|
|
|
|
|
|||||||||||
|
A2 + B2 |
|
|
|
|
|
A2 |
+ B2 |
|
|||||||
1 |
|
1 |
|
|
|
|
2 |
|
2 |
|
|
|||||
6°. Из уравнения прямой проходящей через две точки |
||||||||||||||||
следует условие |
|
расположения |
трех точек |
M1 (x1, y1 ), |
||||||||||||
M2 (x2 , y2 ), M3 (x3 , y3 ) |
одной прямой |
|
||||||||||||||
|
|
y3 − y1 |
= |
x3 − x1 |
. |
|
|
(13) |
||||||||
|
|
|
|
|
|
|||||||||||
|
|
y |
2 |
− y |
|
|
x |
− x |
|
|
|
|||||
|
|
|
1 |
2 |
1 |
|
|
|
|
|
|
|||||
4.1. Написать уравнения прямых проходящих через
точку А(-3,4) параллельно и перпендикулярно к прямой
2x − y −3 = 0 .
Решение. Воспользуемся уравнением пучка прямых (8) и запишем уравнение пучка прямых с центром пучка в точке А
y −4 = k (x +3).
Приводим уравнение прямой к уравнению прямой с угловым коэффициентом у = 2х−3, отсюда угловой
коэффициент прямой k = 2. Если прямые параллельны, то их угловые коэффициенты равны (6). Выбирая из уравнения пучка прямую с угловым коэффициентом k = 2 находим уравнение прямой параллельной данной
2x − y +10 = 0.
Используя условие перпендикулярности прямых (7), находим угловой коэффициент перпендикулярной прямой
106
k = − 12 . Подставляя этот коэффициент в уравнение пучка,
получим уравнение прямой перпендикулярной данной x +2 y −5 = 0.
4.2. Найти прямую, параллельную прямым 2x + y −2 = 0 и2x + y −5 = 0, расположенную между ними и
делящую расстояние между ними в отношении 1:5.
Решение. Возьмем на первой прямой точку А, абсцисса которой равна, например, нулю. Тогда ордината точки А из уравнения прямой равна 2. Проведем из этой точки перпендикуляр до пересечения со второй прямой в точке В
(рис. 2.20).
Рис .3.20 |
k = −2 , |
|
Угловой коэффициент прямой равен |
||
следовательно, угловой коэффициент перпендикуляра kAB = |
1 . |
|
|
|
2 |
Подставляя его и координаты точки в уравнение пучка прямых
(8), находим уравнение перпендикуляра |
y −2 = |
1 |
(x −0) или |
|
|
2 |
|
x −2 y +4 = 0.
Решая уравнение перпендикуляра совместно с уравнением второй прямой, находим точку их пересечения
6 13
B 5 , 5 .
107
Пусть точка С делит отрезок АВ в отношении λ = 15 ,
тогда ее координаты
x = |
x1 +λx2 |
= |
0 + 15 56 |
= 0, 2; y = |
y1+λy2 |
= |
2 + 15 |
135 |
= 2,1. |
|
|
1 |
1+λ |
|
|
||||||
|
1+λ |
|
|
1 |
|
|||||
|
|
|
1+ 5 |
|
|
|
1+ 5 |
|
||
Так как искомая прямая параллельна данным прямым, |
||||||||||
то ее угловой |
коэффициент |
k = −2 . |
Подставляя его и |
|||||||
координаты точки С в уравнение пучка прямых, находим уравнение искомой прямой y −2,1 = −2(x −0, 2) или
2x + y −2,5 = 0.
4.3. Определить вершины и углы треугольника, стороны которого заданы уравнениями x −3y −3 = 0, 7x − y +19 = 0, 3x + y +1 = 0.
Решение. Координаты вершин треугольника А,В,С являются точками пересечения прямых и находятся из совместного решения систем уравнений
|
|
= 0, |
x −3y −3 = 0, |
|
7x − y +19 = 0, |
||||
x −3y −3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
7x − y +19 |
= 0; |
3x + y +1 |
= 0; |
3x + y +1 = 0; |
|||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
||
Обозначим решение первой системы за координаты точки А(-3;-2), второй – В(0;1) и третьей - С(-2;5). Из построения +ABC (рис. 3.21) видно, что прямой АВ соответствует первое уравнение, прямой АС - второе и прямой ВС - третье.
При определении угла А пользуемся формулой (5), полагая за A1, B1 коэффициенты при переменных в уравнении
прямой АВ, а за A2 , B2 коэффициенты в уравнении прямой АС.
108
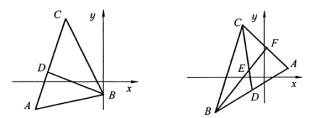
|
Рис. 3.21 |
|
Рис. 3.22 |
|
||||||
|
|
1(−1)−7 (−3) |
|
|
|
|
||||
|
tgA = |
|
|
|
= 2, A = arctg 2. |
|||||
|
1 7 +(−3)(−1) |
|||||||||
При |
определении угла |
В |
за A , B |
формуле (5) |
||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
принимаем коэффициенты в уравнении прямой ВС |
||||||||||
|
|
|
1 1−3(−3) |
|
π |
|
|
|||
|
tgB = |
|
= ∞, |
B = 2 . |
|
|
||||
|
1 3 +(−3) 1 |
|
|
|||||||
Так как сумма углов в треугольнике равна π , то угол |
||||||||||
C = π −arctg2 = arctg |
1 . |
|
|
|
|
|
|
|||
2 |
|
|
|
2 |
|
|
|
|
|
|
4.4. Найти точку пересечения медиан и точку |
||||||||||
пересечения высот треугольника, |
вершины |
которого А(1;4), |
||||||||
B(-9;-8), |
С(-2; 16). |
Написать |
|
уравнение |
биссектрисы |
|||||
внутреннего угла В.
Решение. Медианы пересекаются в одной точке, делящей их в отношении 1:2 от противоположной стороны, которую они делят пополам. Построим треугольник (рис. 3.22) и проведем медиану из точки С. Координаты точки D будут
|
|
|
xD = |
xA + xB |
|
= |
7 −9 |
= −1; yD |
= |
yA + yB |
= 3 −8 |
= −2. |
|
||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
С |
|
2 |
D |
2 |
|
|
|
|
|||||
|
|
|
Зная |
|
координаты точек |
|
|
и |
и |
отношение |
|||||||||||||||||
λ = |
DE |
= 1 |
, |
находим координаты точки пересечения медиан |
|||||||||||||||||||||||
|
EC |
2 |
|
|
−1+ 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
+ 1 |
|
|
|
|||||
|
|
x |
D |
+λx |
|
(−2) |
|
4 |
|
|
|
y |
D |
+λy |
−2 |
(16) |
|
||||||||||
xE = |
|
|
|
|
C |
= |
|
2 |
|
|
= − |
|
; yE |
= |
|
|
|
C |
= |
|
2 |
|
|
= 4. |
|||
|
|
1+λ |
|
|
|
1 |
|
3 |
|
|
1+λ |
|
|
|
1 |
|
|||||||||||
|
|
|
|
|
|
1+ |
|
|
|
|
|
|
|
|
1+ |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
109 |
|
|
|
|
|
|
|
|
|
|
|
|
|

Пользуясь уравнением прямой, проходящей через две
точки, запишем уравнения сторон АВ и ВС |
|
|
|
|
||||||||||||||||||||||
|
y − yA |
= |
|
x − xA |
, |
|
|
y −4 |
= |
|
x −7 |
, |
y = |
3 x − |
5 , |
|||||||||||
|
|
|
|
|
|
|
|
−9 −7 |
||||||||||||||||||
|
yB − yA |
|
xB − xA |
|
|
−8 −4 |
|
|
|
4 |
4 |
|||||||||||||||
|
y − yB |
= |
|
x − xB |
, |
|
|
y +8 |
= |
|
x +9 |
|
, |
y = |
24 x +160 . |
|||||||||||
|
|
|
16 +8 |
−2 +9 |
||||||||||||||||||||||
|
y |
− y |
B |
|
x |
− x |
B |
|
|
|
|
7 |
7 |
|||||||||||||
|
C |
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Угловые коэффициенты перпендикуляров к этим |
||||||||||||||||||||||||||
сторонам находим по формулам (7) |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
kAB = − 4 |
, |
kBC = − |
7 |
. |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
24 |
|
|
|
|
|
|
||||
Подставляя |
найденные |
угловые |
коэффициенты и |
|||||||||||||||||||||||
координаты точек С и А в уравнение пучка прямых (8), находим перпендикуляры к прямой АВ и ВС
y −16 = − |
4 |
(x +2) |
или 4x +3y −40 = 0, |
|
|
|
3 |
|
|
y −4 = − |
|
7 |
(x −7) |
или 7x +24 y −145 = 0. |
|
|
|||
24 |
|
|
||
Решая эти уравнения |
высот совместно, находим |
|||
координаты точки их пересечения (7;4), а это координаты
точки А, т. е. угол А равен |
π и треугольник прямоугольный. |
|||||
|
|
|
|
2 |
|
|
Запишем уравнения сторон АВ и ВС в общем виде: |
||||||
|
|
3x −4 y −5 = 0, 24x −7 y +160 = 0. |
|
|||
Биссектрису BF угла В находим по формуле (12) |
|
|||||
|
3x −4 y −5 = |
24x −7 y +160 , |
9x +13y +185 = 0. |
|||
|
|
9 +16 |
|
576 +49 |
|
|
4.5. Составить уравнение прямой, параллельной |
||||||
прямой 3x +4 y −7 = 0 |
и удаленной от точки А(3;-1) |
на три |
||||
единицы. |
|
|
|
|
|
|
Решение. |
Найдем |
угловой |
коэффициент |
прямой |
||
y = − 3 x + |
7 , |
k = − 3 . |
Воспользовавшись уравнением (8), |
|||
4 |
4 |
4 |
|
|
|
|
проведем через точку А прямую параллельную данной прямой
110
