
2799.Теория механизмов и механика систем машин в задачах и решениях учебно
..pdf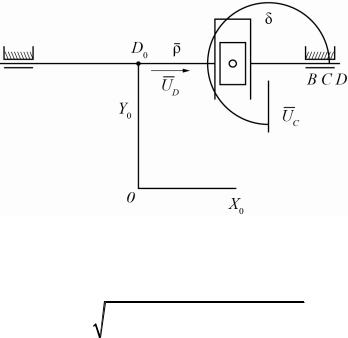
Рис. 3.9. К расчету группы 25
Расчётные формулы:
S = − ( X D |
− X B |
)2 + (YD |
− YB )2 , |
0 |
0 |
0 |
0 |
cos ϕ k= |
( X D |
− X B |
) |
(YD |
− YB |
) |
0 |
0 |
, sin ϕ k= |
0 |
0 . |
||
|
|
S |
|
|
S |
|
3. Кинематика групп 23.
Решение задачи о скоростях. Входы в группу при решении задачи о скоростях:
X B0 1 = X H 1;
YB0 1 = YH 1 (третий и четвертый столбцы таблицы 3.10);
X D0 1 = 0 ; YD0 1 = 0 .
Расчетные формулы:
a11 = cos ϕ |
k ; a12 = −S sin ϕ k ; a21 = sin ϕ k ; |
a22 = S cos ϕ k ; |
|||||
b1 |
= X D |
1 − X B 1; b2 |
= YD |
1 − YB |
1; ∆ = a |
11 a22− а21а12 ; |
|
|
0 |
0 |
0 |
0 |
|
||
|
∆ S1= b a − b a ; ∆ω = a b− a b ; |
||||||
|
|
1 22 |
2 12 |
k |
11 2 |
21 1 |
|
|
|
S1 = |
∆ S1 |
; ω = |
∆ω k . |
|
|
|
|
∆ |
|
|
|||
|
|
|
k |
∆ |
|
||
|
|
|
|
|
|
|
|
71

4. Кинематика группы 23.
Решение задач об ускорениях. Входы в группу при решении задачи об ускорениях:
|
|
|
|
|
|
|
X B 2 = X H 2 ; |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
YB0 2 = YH 2 (пятый и шестой столбцы таблицы 3.10); |
|
|
|
|
|
||||||||||||||
|
|
|
|
X D 2 = 0; YD 2 = 0. |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
Расчетные формулы для |
|
свободных |
членов |
системы |
уравнений |
||||||||||||||
с двумя неизвестными S 2 и ε к : |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
b = X |
D |
2 − X |
B |
2 + 2S1sin ϕ |
k |
ω |
+ |
S cos ϕ |
|
k |
ω |
2 ; |
|
||||||
1 |
|
|
|
|
|
|
k |
|
|
|
k |
|
|||||||
|
|
0 |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b = Y |
2 − Y |
|
2 − 2S1cos ϕ |
k |
ω |
+ |
S sin ϕ |
k |
ω |
2 . |
|
||||||||
2 |
|
D |
B |
|
|
|
|
|
|
k |
|
|
|
k |
|
||||
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты при неизвестных a 11 , a 12 , |
a 21 , |
a 22 останутся те же, |
|||||||||||||||||
что и в задаче о скоростях (табл. 3.9, 3.10). Определитель ∆ |
тоже сохра- |
||||||||||||||||||
нит своё значение. Тогда неизвестные найдём из выражений |
|
||||||||||||||||||
|
∆ S 2= b1a22− b2a12 ; ∆ε k= a11b2− a21b1 ; |
|
|
||||||||||||||||
|
|
|
|
S 2 = |
∆ S 2 |
; ε k = ∆ε k . |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
∆ |
|
|
|
∆ |
|
|
|
|
|
|
|
5. Кинематика группы 25. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Выберем координаты точки D0 (рис. 3.9): |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
X D |
= ... ; YD |
= ... . |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
D вправо, его проекции на оси X0 Y0: |
|
||||||||||||||||
Направим вектор U |
|
||||||||||||||||||
|
|
|
|
UDX |
= 1; UDY |
= 0 . |
|
|
|
|
|
|
|||||||
Угол δ между векторами UD ,UC будет равен 270°, поэтому проекции
вектора UC /UCX = 0 ; UCY = −1.
Уравнение замкнутости контура D0DB в проекциях на оси примет следующий вид:
SD = X B0 ;
SC |
= YD |
− YB . |
(3.80) |
|
0 |
0 |
|
Дифференцируем (3.80) первый раз:
SD1 = X B0 1;
72
SC |
1 = −YB 1. |
(3.81) |
|
0 |
|
Повторное дифференцирование дает
SD |
2 = X B 2 ; |
|
|
0 |
|
SC |
2 = −YB 2. |
(3.82) |
|
0 |
|
Таким образом, решение задач кинематики группы 25 свелось к нахождению координаты точки B0, первых и вторых производных. Эти параметры найдем, применяя вспомогательную задачу первого типа к звену К рассчитанной группы 23 при следующих данных:
a = ...; α = 0 ; X A |
= X D ; YA |
= YD |
; ϕ = ϕ |
k ; |
|
|
0 |
|
0 |
|
|
ω = ω |
k ; ε = ε |
k . |
|
|
|
Расчетные формулы:
где
где
aX = a cos ϕ k ; aY = a sin ϕ k ;
X H = X D0 + aX ; YH = YD0 + aY .
Проекции скоростей точки Н:
X H 1 = aX 1; YH 1 = aY 1;
aX 1= −a sin ϕ k ω |
k ; |
aY 1= a cos ϕ |
k ω |
k . |
|
|||||||
Проекции ускорений точки Н: |
|
|
|
|||||||||
|
|
|
|
|
|
|
X H 2 = aX 2 ; YH 2 = aY 2 , |
|||||
a |
X |
2 = −a |
Y |
1ω − aε |
k |
; a 2 = a |
X |
1ω + a ε |
. |
|||
|
|
k |
Y |
Y |
|
k |
X k |
|
||||
Координаты XH, YH и их первые и вторые производные будут являться входами в группу 25, то есть
X H = X B0 ; YH = YB0 ; X H 1 = X B0 1;
YH 1 = YB0 1; X H 2 = X B0 2 ; YH 2 = YB0 2 .
3.7. Кинематический анализ манипулятора
Прямая задача о положении манипуляторов позволяет определить координаты схвата или его траекторию движения, а также ориентацию схвата вдоль всей траектории. Прямая задача о скоростях состоит в определении абсолютных линейных скоростей точек звеньев манипулятора и угловых скоростей звеньев при заданных законах изменения обобщенных координат. Для кинематического исследования пространственных
73

кинематических цепей существуют различные методы. При исследовании кинематики роботов рациональнее использовать матричный метод.
Рассмотрим манипулятор с тремя степенями свободы. Функцией положения точки D схвата (рис. 3.10) будет зависимость ее радиуса-вектора
ρG(D0) от обобщенных координат и постоянных длин звеньев lВС и lDC. Дан-
ный механизм с незамкнутой кинематической цепью является статически определимым, без избыточных связей (q = 0), поскольку он собирается без натягов. В механизме три одноподвижные пары: две из них вращательные (А, С) и одна поступательная (В). Обобщенных координат три: ϕ 10 – угол поворота звена 1 относительно стойки 4; z21 – линейное перемещение звена 2 относительно звена 1; ϕ 32 – угол поворота звена 3 относительно звена 2. Число степеней свободы W = 3 подтверждается и по формуле Малышева:
5 |
|
= 6 3− 5 3 = 3. |
W = 6n − ∑(6 − i) pi |
− q |
|
i=1 |
|
|
Рис. 3.10. Кинематический анализ манипулятора
74
Система координат O1x(1) связана со звеном 1, вращающимся вокруг оси z(1), система O2x(2) y(2) z(2) – со звеном 2, движущимся прямолинейно относительно звена 1, а система О3х(3) у(3) z3 – со звеном 3, вращающимся вокруг оси z (3). Оси x(1), x(2), x(3) параллельны.
Функция положения в матричной форме имеет такой вид:
ρ (0)= ρ |
(0)ϕ( |
10 |
, z ϕ , |
32 |
), |
|||
D |
D |
|
21 |
|
||||
ρ (0)= |
T |
, T |
|
, |
T ,ρ |
(3) |
, |
|
D |
10 |
21 |
|
32 |
D |
|
|
|
где
|
x(0) |
|
|
|
|
|
|
D(0) |
|
|
|
ρ (0) |
= yD |
; T |
= |
||
D |
z(0) |
|
10 |
||
|
|
|
|||
|
|
D |
|
|
|
|
|
1 |
|
|
|
10
T32 = 0
0
cos ϕ |
10 |
|
|
ϕ |
|
sin |
10 |
|
|
0 |
|
|
0 |
|
|
|
|
0 cos ϕ 32 sin ϕ 32
0
– sinϕ |
10 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
|
|
cosϕ |
10 |
0 |
0 |
|
= |
0 |
1 |
0 |
0 |
|
|
|
|
|
; T |
|
|
|
|
|
; |
||
0 |
|
1 |
0 |
21 |
0 |
0 |
1 |
z |
|
|
|
|
|
|
21 |
||||||||
0 |
|
0 |
|
|
|
|
0 |
0 |
|
|
|
|
1 |
|
|
0 |
1 |
|
|||||
0 |
|
|
0 |
|
|
|
0 |
|
|
– sin |
ϕ |
|
l |
|
|
; ρ (D3)= |
l |
|
|
cosϕ |
|
32 |
|
BC |
|
CD . |
|||
|
32 |
|
0 |
|
|
|
0 |
|
|
0 |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
||||
Последовательным умножением матрицы приводят к равенству
xD(0)
(0)
yD
zD(0)
1
|
–lBC sin ϕ 10− |
lCD sinϕ |
10 cosϕ |
32 |
|
|
|||
|
l |
|
cos ϕ + |
l cosϕ |
|
cosϕ |
|
|
, |
|
= |
BC |
10 |
CD |
10 |
|
32 |
|
|
|
|
|
z21 + lCD sin ϕ |
32 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
следовательно, искомые координаты точки D в неподвижной системе Ох(0) y(0) z(0) будут следующими:
x(0) |
= –l |
BC |
sin |
|
ϕ |
10 |
− l |
|
|
sin |
ϕ |
10 |
cosϕ |
32 |
, |
||||||
D |
|
|
|
|
|
|
CD |
|
|
|
|
||||||||||
y(0) |
= l |
BC |
cos |
ϕ |
10 |
+ l |
|
cos |
ϕ |
10 |
cosϕ |
32 |
, |
||||||||
D |
|
|
|
|
|
|
CD |
|
|
|
|
|
|
|
|||||||
z(0) |
= z |
21 |
+ l |
sin |
|
ϕ |
32 |
. |
|
|
|
|
|
|
|
|
|
||||
D |
|
|
CD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С помощью зависимостей, имея заданный диапазон изменения координат точки D, можно подобрать нужные значения длин звеньев lВС, lCD и диапазоны изменения обобщенных координат ϕ 10, z21 и ϕ 32.
Скорость движения схвата и отдельных звеньев манипулятора определяется не только характером рабочего процесса, но и условиями безопасности для обслуживающего персонала. Если зависимости обобщен-
75

ных координат от времени известны, то скорости можно найти дифференцированием по времени функции положения. Например, для рассмотренного манипулятора с тремя степенями свободы при заданных зависимостях ϕ 10(t), z21(t) и ϕ 32(t) проекции вектора скорости точки D схвата на оси координат получим, дифференцируя выражения
V |
= x(0) |
= –ω |
1 |
cos ϕ |
10 |
(l |
BC |
+ l |
|
|
cos ϕ |
32 |
) + ω |
|
l |
sin ϕ |
10 |
sinϕ |
32 |
, |
|||
Dх |
D |
|
|
|
|
CD |
|
|
|
|
32 CD |
|
|
|
|||||||||
VDy = yD(0) |
= –ω 1 sin ϕ 10 (lBC + lCD cos ϕ 32 ) − ω |
32lCD cos ϕ 10 sinϕ |
32 , |
||||||||||||||||||||
|
|
|
|
VDz = zD(0) |
=V21 + ω 32lCD cosϕ |
32 . |
|
|
|
|
|
||||||||||||
ВеличинуинаправлениевектораскороститочкиD найдемпоформулам |
|||||||||||||||||||||||
|
|
|
V = |
V 2 |
+V 2 |
+V 2 , |
cos α = |
|
VDx |
, |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
D |
|
Dx |
|
Dy |
|
|
Dz |
|
|
|
|
|
VD |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosβ = |
VDy |
|
, cos γ = |
V |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
Dz |
, |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
VD |
|
|
|
|
|
VD |
|
|
|
|
|
|
|
|
где α , β , γ – направляющие углы вектора скорости.
3.8. Графоаналитический метод кинематического исследования рычажных механизмов
Графоаналитический метод, или метод планов, основан на элементах векторной алгебры. При кинематическом исследовании составляются векторные уравнения для скоростей или ускорений механизма в данном положении. Полученные уравнения решаются графически
впорядке присоединения структурных групп к ведущему звену и к стойке. Метод планов применяют тогда, когда имеется схема механизма
вданном положении. Рассмотрим примеры применения графоаналитического метода.
3.8.1. Определение предельных положений механизма (графический метод)
Решение задачи начинают с определения предельных положений механизма, когда рабочий орган механизма занимает крайнее положение. Рассмотрим способы, пользуясь которыми можно в зависимости от типа механизма найти предельные положения.
Для шарнирного четырёхзвенника (рис. 3.11, а, б) предельные положения коромысла 3 будут тогда, когда кривошип 1 и шатун 2 располага-
76

ются на одной прямой. Из точки А в масштабе радиуса кривошипа, а из точки D радиусом коромысла проводим окружности. Затем из А проводим засечки длинами АВ+ВС и ВС–АВ до пересечения с траекторией коромысла в точках С1 и С2. Полученные точки С1 и С2 соединяем с точкой А отрезками, пересекающими окружность кривошипа в точках В1 и В2. Положения механизма, соответствующие схемам AB1C1D и AB2C2D, – предельные (рис. 3.11, б).
Pис. 3.11. Шарнирный четырёхзвенник:
а – кинематическая схема; б – крайние положения
Методика определения крайних положений для кривошипно-пол- зунного механизма (рис. 3.12) аналогична той, которая рассмотрена выше.
77

Для механизма с качающейся кулисой определение предельных положений начинают с построения окружности кривошипа 1 с центром в точке А. Затем проводятся две касательные к этой окружности из точки D – центра качения кулисы 3. Эти прямые и характеризуют схемы AB1D и AB2D механизма, соответствующие двум крайним положениям
(рис. 3.13).
Для более сложных стержневых механизмов крайние положения определяют исходя из конкретной схемы с учётом способов, изложенных выше.
Рис. 3.12. Кривошипно-ползунный механизм: а – кинематическая схема; б – крайние положения
78

3.8.2. Построение плана положений механизма
Построение плана положений механизма проводится в определённом масштабе µl. Масштаб схемы характеризует отношение длины (м) входного звена к отрезку плана положений (мм), соответствующего этому
звену. Например, µl = lОА / (ОА), м/мм.
Рекомендуется масштаб выбирать простым числом, чтобы с ним удобно было проводить вычисления. Выбрав масштаб, определяют длины отрезков схемы, соответствующие остальным звеньям. Например,
ВС = lВС /µl, мм, CD = lCD / µl, мм, и т.д.
После выбора масштаба строятся крайние положения механизма, одно из которых принимается за начальное, соответствующее началу рабочего хода. Таким образом, за нулевое положение (начало отсчёта) принимается положение кривошипа, соответствующее начальному.
Рис. 3.13. Кулисный механизм:
а – кинематическая схема; б – крайние положения звена
79
Построение всех текущих положений механизма ведётся в порядке присоединения структурных групп методом засечек в соответствии с направлением движения ведущего звена. На рис. 3.14 изображена схема кулисного механизма в 12 положениях в масштабе µl.
Под системой координат S = f(t) строим систему координат V = f(t) c тем же расположением положений φ1, φ2 и т.д. На оси φ левее O откладывается отрезок H1 произвольной величины. При этом следует учесть, что чем больше H1, тем больше величины ординат диаграммы V = f (t1). Из точки O1 проводим лучи O1 – 1', O1 – 2', O1 – 3' и т.д., параллельные хордам 1 и т.д. Проведённые лучи отсекают на оси ординат отрезки O – 1', O – 2', O – 3' и т.д., величины которых откладываются по вертикали из середин отрезков 0–1, 1–2, 2–3 и т.д. оси Oφ. Соединив полученные точки плавной кривой, получают график скорости точки (рис. 3.15, б). Масштаб скорости и его аналога:
µV = (µS/H1 · µφ) ω1 = µS/µt · H1;
µVφ = µS / H1· µφ.
Имея график V = f (t), можно найти значение скорости в любом положении кривошипа. Например, для 5-го положения
VE5 = µV (y5).
Аналогичным образом строится график ускорения точки (рис. 3.15, в). В случае прямолинейного движения точки – это полное ускорение, иначе – тангенциальное. Масштаб ускорения мс–2/мм для диаграммы таков:
µa = µV /µt · H2 = (µV /µφ · H2) ω12.
На рис. 3.15 показана диаграмма движения точки Е выходного звена: а) перемещение и путь: S = f (f);
б) скорость точки Е: V = f (t); в) ускорение точки Е: a = f (t).
80
