1505

Потери мощности на трение в обращенном механизме найдем через его коэффициент полезного действия, верхний индекс указывает неподвижное звено, здесь – водило.

Мощность, потерянная на преодоление сил трения в зацеплениях, равна

NT = N1 (1 − η 1(nB ) ).

Мощность на валу ведущего колеса

Коэффициент полезного действия зубчатого механизма, составленного из двух колес, находят по формуле

η = 1− 2, 3 f z2 ± z1 , z1 z2

здесь знак плюс соответствует внешнему зацеплению, знак минус – внутреннему; z – число зубьев. Коэффициент трения в зацеплении f = = 0,05…0,10. Если ведущее колесо – водило, то

η (Bn1)= η 1(n) .

1B

Коэффициенты полезного действия механизмов зависят от многих не учтенных нами параметров, поэтому точное значение их можно установить только экспериментально.

391

Задачи по КПД планетарного механизма

12.1. Определить момент МН, снимаемый с вала водила Н планетарного одноступенчатого редуктора, если к валу его колеса 1 подводится мощность N1 = 750 Вт. Колесо 1 вращается со скоростью n1 = = 700 об/мин. Числа зубьев

колес: z1= z2' = 40, z2 = z3 = 30;

коэффициент полезного действия каждой пары колес η =

=0,9.

12.2.Определить момент

МН, снимаемый с вала водила Н одноступенчатого планетарного редуктора, если к валу его колеса 1 подводится мощность N1 = 750 Вт и колесо

колес: z1 = z2 = 50, z3= 60, ко-

эффициент полезного действия каждой пары колес η = 0,9.

12.3. Определить коэффициент полезного действия планетарного механизма лебедки, если ведущим является вал водила Н, ведомым – вал колеса 1. Числа зубьев колес

равны z1 = 65, z2 = 62, z2' = 63, z3 = 66. Коэффициент полезно-

го действия каждой пары ко-

лес η = 0,98.

392

13. ОСНОВЫ ВИБРОЗАЩИТЫ МАШИН

Повышение быстроходности машин, характерное для развития машиностроения, неизбежно приводит к повышению уровня создаваемых динамических воздействий. Это проявляется в увеличении динамических напряжений в элементах машин, снижении их несущей способности, появлении усталостных напряжений.

Особенно сложны проблемы виброзащиты в современных транспортных средствах (летательные аппараты, колесные и гусеничные машины, морские суда и т.д.). Создатели новых машин могут по-разному подходить к решению проблемы виброзащиты. Так, защищая водителя от вибрационных воздействий, конструктор может пойти по пути снижения колебаний массы со всеми установленными на нем агрегатами или по пути уменьшения колебаний только одного сиденья механика-водителя. Очевидно, что во втором случае эффективность решения достигается более простыми техническими средствами, чем в первом случае.

Виброзащита – это совокупность методов и средств, уменьшающих вредное влияние вибраций. Создание виброзащитных устройств, позволяющих эффективно решать поставленные перед ними задачи при ограниченных массовых и геометрических характеристиках, является сложной технической задачей, решение которой оказывается возможным только при всестороннем учете характера возмущений и особенностей динамики создаваемых систем. Все это привело к возникновению и развитию большого самостоятельного раздела динамики машин – теории виброзащитных систем.

13.1. Основные методы виброзащиты. Виброизоляция

Уменьшение интенсивности колебаний объекта может быть достигнуто разными способами.

1.Уменьшением уровней механических воздействий, возбуждаемых источником (такой способ виброзащиты называется снижением виброактивности источника). Для этого осуществляют уровновешивание рычажных механизмов и балансировку роторов, о чем речь шла выше.

2.Изменением конструкции объекта, при котором заданные механические воздействия будут вызывать менее интенсивные колебания объекта или отдельных его частей (этот метод называется внутренней вибро-

защитой объекта).

393

3.Присоединением к объекту дополнительной динамической системы, изменяющей характер его колебаний. Такая система называется динамическим гасителем колебаний, а метод защиты, основанный на ее при-

менении, – динамическим гашением колебаний.

4.Установкой между объектом и источником колебаний дополнительной системы, изменяющей характер его колебаний. Этот метод виброзащиты называется виброизоляцией, а устройства, устанавливаемые между источником и объектом, – виброизоляторами (виброизолирующими устройствами).

Действие виброизоляции сводится к ослаблению связей между источником и объектом; при этом уменьшаются динамические воздействия, передаваемые объекту.

Рис. 13.1. Схема вибрационной системы

Ослабление связей обычно сопровождается возникновением некоторых нежелательных явлений:

•увеличением статических смещений объекта относительно источника;

•увеличением амплитуд относительных колебаний при низкочастотных воздействиях.

Поэтому применение виброизоляции как метода виброзащиты в большинстве случаев связано с нахождением компромиссного решения, удовлетворяющего всей совокупности требований.

Давайте рассмотрим случай виброизоляции с помощью упругих амортизаторов.

394

13.2. Случай силового возбуждения

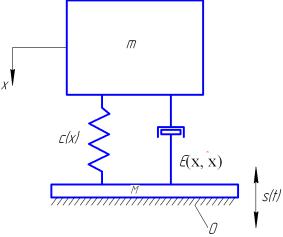
Между основанием и амортизируемым объектом устанавливается упругий амортизатор (или упругие амортизаторы).

К амортизируемому объекту приложена внешняя сила F(t). Ставится задача снизить динамические силы, передаваемые на основание, за счет введения в систему упругих амортизаторов.

Поведение системы описывается следующим дифференциальным уравнением:

F(t) – внешняя сила, приложенная к объекту; R(x, x ) – сила, приложенная к массе со стороны упругого амортизатора.

Простейшим примером таких воздействий может служить гармоническая вынуждающая сила F = F0(sinωt + φ), где F0 – амплитуда колебаний; ω– круговаячастота(рад/с).

Рис. 13.2. Зависимость вынуждающей силы от периода колебаний

В более сложных случаях воздействие на массу т может быть описано конечной (или бесконечной) суммой гармонических компонентов. Тогда

N

F (t) = ∑ Fi (cos ω it+ ϕ 1 ) .

i=1

Такое вибрационное воздействие принято называть полигармоническим. Ограничимся рассмотрением случая, когда на массу т действует гармоническая вынуждающая сила, описываемая уравнением

395

13.3. Этапы решения задач виброзащиты

Решение задач виброзащиты машин и механизмов включает следующие этапы:

•построение модели объекта;

•формирование критериев качества;

•изучение реакции объекта на заданное внешнее воздействие;

•сравнение по заданному критерию результирующих показателей

сдопустимыми величинами.

Простейшие задачи виброизоляции возникают в том случае, когда совокупность сил в реальном упругом амортизаторе может быть с достаточной точностью описана как линейная функция координаты х и скорости x :

Коэффициент с принято называть жесткостью амортизатора, a ε – коэффициент вязкого трения (демпфирования). С учетом (13.3) уравнение (13.1) примет вид

Обозначим c = ω 2 ; ε = 2n и перепишем (13.4) следующим образом:

Ограничимся анализом работы виброзащитной системы в установившемся режиме. В этом случае решение уравнения (13.5) может быть представлено в виде

где А – амплитуда колебаний массы т; γ – сдвиг фаз между колебаниями массы т и внешней силой F(t). При этом амплитуда колебаний

и сдвиг фаз колебаний массы т1 и силы F(t)

Оценку качества виброизоляции целесообразно проводить, сопоставляя амплитудное значение силы R0, развиваемой в амортизаторе и, следовательно, передаваемойнаоснование, самплитуднымзначениемвнешнейсилыFQ.

396

Отношение амплитудного значения силы R0 к амплитудному значению внешней силы F0 называется коэффициентом виброизоляции

KR = R0 . F0

Амплитудное значение силы, развиваемой в упругом амортизаторе, показано на рис. 13.3:

397

13.4. Кинематическое возбуждение объекта

Если перед проектировщиком ставится задача защиты объекта, находящегося на вибрирующем основании (рис. 13.4), то в простейшем случае с учетом сделанных выше предположений данная задача сводится к анализу динамической схемы, представленной на рис. 13.1.

Дифференциальное уравнение, описывающее колебание массы т, может быть записано в виде

mx + ε ( x− s)+ c ( x− s)= 0 .

смысл гармонической возмущаю-

щей силы. Очевидно, что анализ уравнения (13.7) аналогичен анализу уравнения (13.4), проведенному ранее. Совпадают и вытекающие из этого анализа рекомендации.

13.5. Динамическое гашение колебаний

Динамический гаситель, присоединяемый к объекту, формирует дополнительные динамические воздействия, прикладываемые к объекту в точках присоединения гасителя. Динамическое гашение осуществляется при таком выборе параметров гасителя, при котором эти дополнительные воздействия частично уравновешивают (компенсируют) динамические воздействия, возбуждаемыеисточником.

Схема простейшего динамического виброгасителя представлена на рис. 13.5.

На массу m1, упруго соединенную с основанием, действует приложенная сила F(t), которую будем в дальнейшем полагать монохромати-

ческой.

F = F0cosωt.

398

Задача ставится следующим образом: выяснить возможность снижения амплитуды колебаний массы m за счет введения дополнительной массы m2, упруго соединенной с массой m1. С целью упрощения задачи полагаем, что система недиссипативна, т.е. рассеяния энергии в упругих связях не происходит.

Дифференциальные уравнения, описывающие движения масс m1 и m2,

Поскольку система недиссипативна, то колебания отдельных масс либо совпадают по фазе с внешней возмущающей силой, либо находятся с ней в противофазе (сдвиг 180°).

Частное решение системы (13.8) может быть представлено в виде

x1 =Acosωt, x2 = θAcosωt, (13.9)

где θ – коэффициент распределения амплитуд колебаний. Величину θ определяем, подставив соотношение (13.9) во второе уравнение (13.8):

Решение системы линейных дифференциальных уравнений может быть сведено к интегрированию одного линейного дифференциального уравнения второго порядка вида (13.12), в результате которого вычислим амплитуду А:

399

Знаменатель дроби может обращаться в нуль при изменении параметров системы, т.е.

Данное уравнение является частным уравнением системы, у которой два корня с1, и с2, являющиеся частотами собственных колебаний системы. В нуль может обращаться и числитель дроби в правой части соотно-

шения (13.13), т.е.

При выполнении соотношения (13.14) амплитуда А колебаний массы m1 обращается в нуль, и, следовательно, масса m становится неподвижной. Это явление называется антирезонансом, а частота ωA, при которой это происходит, – частотой антирезонанса.

Частота антирезонанса совпадает с частотой собственных колебаний массы т2 при неподвижной массе m1. Неподвижность массы т1 в точке антирезонанса гарантируется только выполнением соотношения (13.14).

Определим амплитуду колебаний массы т2. Из соотношения (13.13) и (13.14) получим

Очевидно, что если масса т2 оказывается малой, то при фиксированной ωA жесткость с2 также мала, большой оказывается амплитуда θА. Чтобы ее уменьшить, приходится увеличивать массу т2.

400