1505

Как известно из курса сопротивления материалов, прогиб вала от действия центробежной силы при известных его модуле упругости материала E и моментеинерцииI поперечногосеченияравенy = Fц/ C = Fцl3/48EI.

Центробежная сила уравновешивается силой упругости звена. Тогда

Из анализа зависимости (9.22) следует, что прогиб вала возрастает при приближении значения ω к значению величины C / m . Следовательно, критическое значение угловой скорости, при которой прогиб теоретически становится равным бесконечности, равно

Связав ось ординат y с вращающимся диском, получим из (9.22)

Из зависимости (9.24) следует, что с увеличением скорости вращения прогиб звена уменьшается и центр масс звена стремится к установке на геометрической оси его вращения.

9.5. Особенности колебаний поступательно движущихся звеньев

Учет упругости поступательно движущихся звеньев позволяет подобрать их размеры и массы таким образом, чтобы устранить возможные погрешности вихзаконахдвижения. Рассмотримвлияниеупругостизвеньевнафункциюперемещения толкателя кулачкового механизма, для условий безударной работы которогооченьважнаточностьреализациизаданногодвижениятолкателя.

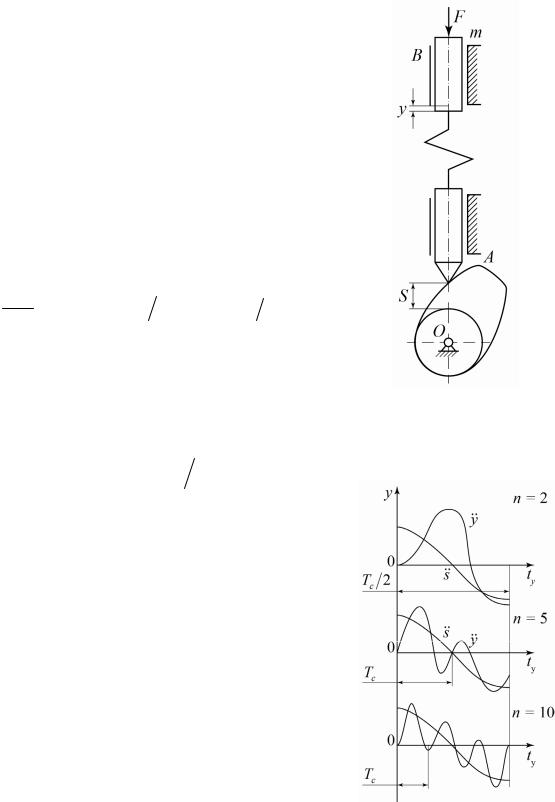
В реальных кулачковых механизмах жесткость кулачков намного больше жесткости толкателей. Для обеспечения замыкания кинематической пары «кулачок – толкатель» в конструкции узла толкателя предусматривают пружину (рис. 9.7). Под действием силы технологического сопротивления, действующей на толкатель, и давлением кулачка толкатель деформируется. С учетом его деформации дифференциальное уравнение движения упругого толкателя будет иметь вид

351

352

На рис. 9.8 приведены графики функции ускорений толкателяy для раз-

ных значений n в сравнении с функцией ускорений S , заданных без учета упругости толкателя. Как видно из графиков, уменьшение периода собственных колебаний Tc по сравнению со временем удаления толкателя ty ведет

ксущественнымискажениямпредставленияозаконедвижениятолкателя.

9.6.Демпфирование свободных колебаний звеньев

Вреальных механизмах относительное движение звеньев всегда сопровождается действием сил сопротивления движению. К ним относят силы трения в кинематических парах, электромагнитного сопротивления в электрических машинах, гидродинамического сопротивления в гидромашинах и т.п. Поэтому колебательные движения звеньев всегда сопровождаются действием сил неупругого сопротивления. Эти силы демпфируют колебания, т.е. способствуют их гашению. При определении параметров колебательного процесса величину силы демпфирования в первом приближении принимают пропорциональной скорости движения. Закон движения будет описываться дифференциальным уравнением

где k – коэффициент пропорциональности.

Обозначив kg / G = 2n, получим дифференциальное уравнение для свободных колебаний звена с демпфированием

Постоянная α определяется из условия, что решение (9.32) удовлетворяет уравнению (9.31). Определяя dx/dt, d2x/dt2 и подставляя их выражения в уравнение (9.31), получим

В решении (9.34) при n < ωc, что соответствует случаю, когда силы демпфирования достаточно малы, получим два комплексных корня α1 = – n + iβ

353

иα2 = – n – iβ (при β = ω 2c− n2 и i = −1 ). Подставляя выражения для них

врешение (9.32), найдем частные решения. Общее решение получим как суммучастныхрешенийввиде

Из анализа полученного выражения следует, что при действии демпфирующей силы период колебаний возрастает. При n << ωc это возрастание незначительно и может не учитываться. Множитель e–nt в зависимости (9.35) убывает с ростом t. Следовательно, колебания при действии демпфирующей силы затухают со временем (9.10). Определяя постоянные в выражении (9.35), получим после преобразования выражение амплитуды колебаний при действии демпфирующей силы

которое не содержит периодических членов. Следовательно, при достаточно больших значениях демпфирующих сил колебаний звена нет.

9.7.Демпфирование вынужденных колебаний звеньев

Вмеханизмах со сложными кинематическими схемами и сложными конструкциями звеньев трудно выделить источник силы, вызывающей вынужденные колебания. Поэтому в конструктивную схему механизма вводят специальные устройства – демпферы (гасители). С учетом демпфирующих сил для вынужденных колебаний звеньев получим

где q sin ω вt – законизменениясилы, вызывающейвынужденныеколебания. Общимрешениемдифференциальногоуравнения(9.37) будетвыражение

Последние два слагаемых в уравнении (9.38) соответствуют частному решению

354

для вынужденных колебаний звеньев. Подставляя значения амплитуды для вынужденных колебаний из (9.39) в выражение (9.37), после преобразований найдем

Динамический коэффициент при действии демпфирования меняется в широких пределах в зависимости от соотношения частот собственных и вынужденных колебаний. Дифференцируя выражения для kд по (ωв / ωс) и приравнивая производную к нулю, получим выражение для максимального значения динамического коэффициента.

355

10. УРАВНОВЕШИВАНИЕ РЫЧАЖНЫХ МЕХАНИЗМОВ

10.1. Общие сведения

Большинство звеньев рычажных механизмов совершает вращательное, поступательное или плоское движение. Звенья, совершающие плоское движение, входят в поступательные и вращательные пары.

К таким звеньям относятся шатуны двигателей внутреннего сгорания. Наиболее тяжёлые их части, кривошипные и поршневые головки, при решении задачи уравновешивания разделяют (одну из них относят

к кривошипу, другую – к поршню) и вместе с ними уравновешивают. Для вала, как для ротора, определяется масса противовеса. Задача

уравновешивания поршня и поршневой головки шатуна сложнее.

Если допустимы большие габариты, можно расположить цилиндры симметрично (рис. 10.1) и силы инерции попарно уравновесятся.

Рис. 10.1. Кинематическая схема компрессора

В высокооборотных двигателях внутреннего сгорания силы инерции поршней уравновешивают противовесами на зубчатых колёсах, вращающимися на валу двигателя (рис. 10.2).

Поршень движется по закону

S = r (l – cosφ + 0,5λsin²φ),

где r – длина кривошипа l; l – длина шатуна 2; λ – его удлинение; λ = l/r. Скорость поршня

V = ds/dt = ωr (sinφ + cos2φ),

ускорение поршня

a = dν/dt = ω2r (cosφ + λcos2φ).

Сила инерции поршня и присоединённой к нему головки шатуна, как и их ускорение, состоит из двух составляющих, называемых силой инер-

ции первого порядка

F1И = −mrω 2 cos ϕ

и силой инерции второго порядка

F2И = −mrω 2 cos 2ϕ .

356

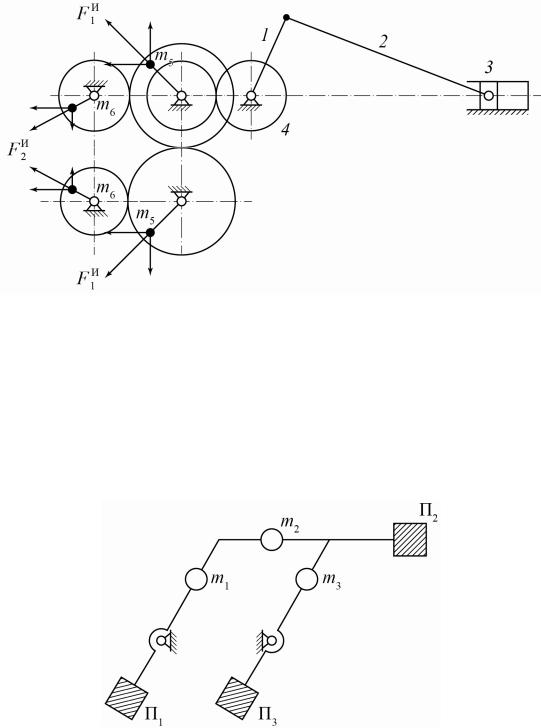
Системапротивовесов, котораяихуравновешивает, показананарис. 10.2.

Рис. 10.2. Система противовесов

Противовесы массой m5 вращаются в разные стороны с угловой скоростью кривошипа, противовесы массой m6 – со скоростью вдвое большей.

Вертикальные их составляющие уравновешивают друг друга, горизонтальные – силы инерции поршня. На реальных двигателях система компактна.

На стационарных машинах силы инерции всех вращающихся звеньев уравновешивают противовесами, их размещение показано на рис. 10.3.

Рис. 10.3. Уравновешивание вращающихся звеньев на стационарных машинах

Центры масс кривошипа и коромысла с противовесами лежат в неподвижных точках О1 и О3. Шатун уравновешен частично.

357

10.2. Статическое уравновешивание рычажных механизмов

Если главный вектор инерции FS = 0, то такой механизм называется статически уравновешенным. Если главный момент сил инерции МS = 0, то механизм называется моментно-уравновешенным.

Рассмотрим случай, когда надо уравновесить механизм статически, т.е. FS = 0 (рис. 10.4, звенья 1–4). Этого можно добиться только тогда, когда aS = 0, так как S → A, FS = –maS, где aS – ускорение центра масс S звена.

Когда центр масс совмещён с A, то он становится неподвижным. Этого добиваются с помощью двух противовесов, один из которых устанавливают на продолжении шатуна, а другой – на продолжении кривошипа.

Для того чтобы рассчитать массы противовесов, применяют метод замещающих масс, суть которого заключается в том, что масса каждого звена условно распределяется по двум точкам (рис. 10.5).

При этом масса выбранного звена разносится по точкам A и B так, чтобы положение центра масс не изменилось.

m = mA + mB,

lAB = lAS + lBS,

mA lAS = mB lBS.

Масса 3-го звена сосредотачивается в точке С (рис. 10.6)

Масса 2-го звена распределятся по шарнирам В и С. Если на продолжении звена 2 поставить противовес массой mп2 на расстоянии от точки В, равном lп2, то центр масс звеньев 2 и 3 переместится в точку В, при этом

358

mп2lп2 = (m2C + m3C) lBC.

В этом случае либо задаются массой противовеса и определяют lп2, либо задаются lп2 и определяют массу противовеса

mп1lп1 = (m1B + mп2 + m2B + m2C + m3C) lAB.

После всех указанных мероприятий центр масс переместится в точку A, однако не всегда конструктивно можно установить противовес на продолжении шатуна, поэтому ограничиваются установкой противовеса на звене l. Тогда центр масс системы смещают на линию AC, и этот центр масс перемещается с постоянным ускорением а = const.

В этом случае механизм – частично статически уравновешенный (рис. 10.7), его нежелательно устанавливать на высоком фундаменте, так как главный вектор сил инерции создаёт опрокидывающий момент, что недопустимо.

В четырёхшарнирном механизме (рис. 10.8) центр масс системы разносится по точкам A и D, а противовесы устанавливаются на продолжении звеньев 1 и 3.

359

Задачи по уравновешиванию рычажных механизмов

10.1. Определить массу противовеса mп, который надо установить на вращающийся вал для уравновешивания сил инерции грузов с массами m1, m2, m3 и m4, лежащих в одной перпендикулярной к оси вала плоскости, если координата центра масс Sп противовеса ρп = 15 мм; массы грузов m1 = 5 кг, m2 = 7 кг, m3 = 8 кг, m4 = 10 кг; расстояния от оси вала до центров масс S1, S2, S3 и S4 грузов: ρ1 =

= 10 мм, ρ2 = 20 мм, ρ3 = 15 мм, ρ4 = 10 мм;

углызакреплениягрузовα12 = α23 = α34 = 90°.

10.2. Определить массы противовесов mпI и mпII, которые надо установить в плоскостях исправления I и II для уравновешивания сил инерции грузов с массами m1, m2, m3 и m4, лежащих в плоскости, содержащей ось вала, если координаты центров масс SпI

и SпII противовесов равны ρпI = 50 мм, ρпII = = 40 мм. Массы грузов: m1 = 2 кг, m2 = 3 кг,

m3 = 2 кг, m4 = = 4 кг; координаты центров

масс S1, S2, S3 и S4 грузов: ρ1 = 10 мм, ρ2 = = 15 мм, ρ3 = 12 мм, ρ4 = 20 мм; расстояние

между грузами l12 = l23 = l34 = 100 мм.

10.3. Определить массы противовесов mпI и mпII и углы их закрепления βI и βII (отсчитываемые от линии OS2 в направлении против движения стрелки часов) для уравновешивания сил инерции грузов m1, m2, если координаты центров масс S1 и S2 противовесов ρпI = ρпII = 10 мм. Массы грузов: m1 = 1,0 кг, m2 = 2,0 кг. Расстояния

360