1505

10.4. Определить реакции RA иRB вподшипниках вала от сил инерции грузов, массы которых равны m1 = 1,0 кг, m2 = = 0,5 кг, m3 = 0,25 кг; центры масс всех грузов расположены в плоскости, содержащей ось вращения вала АВ. Координаты центров

масс S1, S2, и S3 грузов: ρ1 = 100 мм, ρ2 = 100 мм, ρ3 = 200 мм; расстояния грузов от под-

шипника А: lA1 = 100 мм, lA2 = 300 мм, lA3 = = 400 мм; расстояние между опорами А и В

L = 500 мм, угловаяскоростьвалаω= 20 с–1.

10.5. Определить массы противовесов mпI и mпII, которые надо установить в плоскостях исправления I и II для уравновешивания сил инерции грузов m1 и m2, лежащих в плоскости, содержащей ось вращения вала, если координаты центров масс SпI и SпII противовесов равны ρпI = ρпII = 100 мм. Массы грузов: m1 = 20 г, m2 = 10 г, координаты центров масс S1 и S2 грузов от плоскости исправления I: lA1 = 200 мм, lA2 = 400 мм, расстояние между плоскостями исправления

L = 600 мм; ρ1 = ρ2 = 100 мм.

10.6. Определить массы противовесов mп1 и mп2, которые необходимо установить на кривошипе АВ и шатуне ВС для полного уравновешивания главного вектора сил инерции всех звеньев кривошипно-ползун- ного механизма, если координаты центров масс S1 и S2 этих противовесов lAS'1 =

=500 мм, lBS'2 = 200 мм, lAB = 100 мм, lBC =

=300 мм; координаты центров масс S1, S2

и S3 звеньев lAS1 = 75 мм, lBS2 = 200 мм, lCS3 = 100 мм; массы звеньев равны m1 =

= 0,1 кг, m2 = 0,7 кг, m3 = 0,8 кг.

361

10.7. Предполагая, что все силы инерции звеньев приведены к общему центру масс S, определить точку приложения, модуль и направление главного вектора сил инерции подвижных звеньев кривошипно-ползун- ного механизма при φ1=45°, если lAB = = 50 мм, lBC = 150 мм; координаты центров масс S1, S2 и S3 звеньев равны

lAS1 = 20 мм, lBS2 = 75 мм, lCS3 = 0, мас-

сы звеньев m1 = 2,5 кг, m2 = 1 кг, m3 = = 1,5 кг. Угловая скорость кривошипа АВ постоянна и равна ω1 = 100 с–1.

Указание. Предусматривается графическое решение, поэтому предварительно надо построить схему механизма, одна точка которого копирует движение общего центра масс подвижных звеньев.

10.8. Определить модуль и направление главного вектора сил инерции подвижных звеньев криво- шипно-ползунного механизма при

φ1 = 45°, если lAB = 50 мм, lBC =150 мм;

координаты центров масс S1, S2 и S3 звеньев равны lAS1 = 10 мм, lBS2 =

=75 мм, lCS3 = 0, массы звеньев m1 =

=2,5 кг, m2 = 1 кг, m3 = 1,5 кг. Угло-

вая скорость кривошипа АВ постоян-

на и равна ω1 = 100 с–1.

10.9. Масса ползуна 3 кривошип- но-ползунного механизма m3 = 0,4 кг. Подобрать массы m1 и m2 шатуна ВС и кривошипа АВ таким образом, чтобы главный вектор сил инерции всех звеньев механизма был уравновешен. Координаты центров масс S1 и S2 звеньев АВ и ВС равны lAS1 = 100 мм,

lBS2 = 100 мм, если lAB = 100 мм, lBC = 400 мм.

362

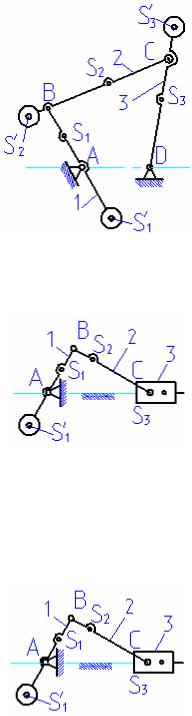
10.10. Определить массы противовесов mп1, mп2, mп3, необходимых для полного уравновешивания главного вектора сил инерции механизма шарнирного четырехзвенника, если lAB = = 120 м, lBC = 400 мм, lCD = 280 мм, координаты

звеньев m1 = 0,1 кг, m2 = 0,8 кг, m3 = 0,4 кг, ко-

ординаты центров масс S'1, S'2, S'3 противовесов

lAS'1 = 100 мм, lBS'2 = 200 мм, lCS'3 = 130 мм. Зада-

чу решить, полагая, что общий центр масс подвижных звеньев механизма должен быть неподвижен и лежать в точке А.

10.11. Определить массу противовеса mп, который необходимо установить на кривошипе АВ кривошипно-ползунного механизма для полного уравновешивания вертикальной составляющей главного вектора сил инерции всех звеньев механизма, если координата центров масс S'1 этого противовеса lAS'1 = 600 мм; размеры звеньев lAB = 100 мм, lBC = 500 мм; координа-

ты центров масс S1, S2 и S3 звеньев lAS1 = 75 мм, lBS2 = 150 мм, lCS3 = 100 мм; массы звеньев рав-

ны m1 = 0,3 кг, m2 = 1,5 кг, m3 =2,0 кг.

10.12. Определить массу mп противовеса, который необходимо установить на кривошипе АВ кривошипно-ползунного механизма для уравновешивания сил инерции массы кривошипа и той части массы шатуна ВС, которая может быть отнесена к точке В после разноса (статического) его массы на две, сосредоточенные в точках В и С, если координата центра масс S'1 противовеса lAS'1 = 600 мм. Размеры звеньев lAB = 100 мм, lBC = 500 мм; координаты

центров масс S1, S2 и S3 звеньев lAS1 = 75 мм, lBS2 =150 мм, lCS3 = 100 мм; массы звеньев рав-

ны m1 = 0,3 кг, m2 = m3 = 1,5 кг.

363

10.13. Определить массу mп противовеса, который необходимо установить на кривошипе АВ кривошипно-ползун- ного механизма для уравновешивания главного вектора сил инерции звеньев механизма, если координата центра масс

S'1 противовеса lAS'1 = 600 мм. Размеры звеньев lAB = 100 мм, lBC = 500 мм; координаты центров масс S1, S2 и S3 звеньев

lAS1 = 75 мм, lBS2 = 200 мм, lCS3 = 100 мм;

массы звеньев равны m1 = 0,3 кг, m2 = = 1,5 кг, m3 = 3,0 кг.

Указание. Предварительно развести статически массу шатуна на две точки, совпадающие с точками В и С. У ползуна уравновешивать только силу инерции первого порядка.

10.14. Определить массы mп1 и mп2 противовесов, которые надо установить на колесах а и б для полного уравновешивания сил инерции первого порядка звеньев кривошипно-ползун- ного механизма, если координаты центров масс SпI и SпII противовесов lASп1 =

= lDSп1 = 50 мм, а радиусы колес одинаковы. Размеры звеньев: lAB = 100 мм,

lBC = 400 мм; координаты центров масс

S1, S2 и S3 звеньев lAS1 = 30 мм, lBS2 = = 100 мм, lCS3 = 0; массы звеньев равны

m1 = 2,5 кг, m2 = 1,0 кг, m3 = 3,0 кг.

Указание. Решить задачу в следующей последовательности:

а) уравновесить силы инерции звеньев механизма в вертикальном направлении;

б) уравновесить силы инерции звеньев в горизонтальном направлении. Принимать во внимание только силы инерции первогопорядка.

364

11.УРАВНОВЕШИВАНИЕ РОТОРОВ

Вмашиностроении и приборостроении любое вращающееся тело называют ротором (шкивы, зубчатые колеса, звездочки цепных передач, соединительные муфты, маховики, диски сцепления, шлифовальные круги, колеса автомобиля, диски турбин и т.п.). Роторы многих приборов вращаются с частотой 75 тыс. об/мин; роторы центрифуг, предназначенных

для получения биологических эмульсий, имеют частоту вращения 500 тыс. об/мин. При конструировании таких роторов необходимо решить задачи динамического синтеза, связанные с распределением масс по условиям уменьшения динамических реакций в опорах ротора.

11.1. Статическая неуравновешенность ротора

Рассмотрим двухопорный ротор, вращающийся относительно оси OZ (рис. 11.1) с угловой скоростью ωG и угловым ускорением ε .

Рис. 11.1. Схема двухопорного ротора

В точках O1, O2 расположены опоры ротора. Выберем систему координат O1XYZ, вращающуюся вместе с ротором. Положение элементарной массы dm в теле ротора определим радиус-вектором r , проведенным из начала координат.

Положение этой массы можно характеризовать и вектором eG, который является кратчайшим расстоянием до оси вращения. Вектор eG называется эксцентриситетом неуравновешенной массы. Произведение массы на ее эксцентриситет называется элементарным дисбалансом: dD = eG dm .

Элементарныйдисбаланснаправленпоэксцентриситету. Через Fo1 x , Fo1 y , Fo2 x , Fo2 y обозначеныпроекциидинамическихреакцийвопорахротора.

Измеханикиизвестновыражениедлясилыинерцииэлементарноймассы:

365

Распишем проекции векторов, входящих в выражение (11.1):

Интегрируя по всему объему, определим проекции силы инерции:

гдеxs, ys – координаты центра масс ротора; m – масса ротора. Далее получаем модуль вектора:

F = F 2 x + F 2 y = m (xs2 + ys2 ) ω 4+ ε 2= mecm ω +4ε 2 . (11.7)

Произведение массы ротораG на эксцентриситетG его центра масс называется дисбалансом ротора D = meGcm . Вектор F называется главным век-

тором сил инерции ротора, он приложен в его центре масс S.

Таким образом, статическая неуравновешенность ротора характеризуется наличием дисбаланса его массы или смещением центра масс с оси вращения. Возникающий при этом вектор F вG общем случае не совпадает по направлению с вектором дисбаланса D . При постоянной частоте вращения направления этих векторов совпадают.

11.2. Моментная неуравновешенность ротора

Момент силы инерции элементарной массы относительно начала координат находим из выражения

− ε (x2 + y2 )dm].

366

Проинтегрировав в проекциях, найдём:

Интегралы в последних выражениях представляют собой центробежные Jxz, Jyz и осевой Jz моменты инерции. Получаем:

Модуль главного момента M сил инерции ротора находится из выражения:

Таким образом, моментная неуравновешенность ротора характеризуется наличием главного момента дисбалансов, направленного перпендикулярно оси вращения.

Величина и направление главного вектора сил инерции F не зависят от центра приведения элементарных сил, а величина и направление главного момента сил инерции M зависят (на рис. 11.1 он приложен в точке O1).

Для выделения проекций массово-геометрических характеристик из проекций силовых (11.4), (11.5) и моментных характеристик (11.12), (11.13) достаточно принять ω = 1 (аналог скорости, безразмерная величина) и ε = 0 (аналог ускорения). При этих условиях получим

Dy = 0 ; MDx = 0 ; MDy = 0 ), то нулю равны главный вектор сил инерции, и главный момент сил инерции ротора.

367

Следовательно, условия, при которых проекции динамических реакций в опорах ротора будут равны нулю, запишутся в виде

реакции не влияет, и его можно не принимать во внимание.

Виды неуравновешенности ротора можно различать по его массогеометрическим характеристикам:

– при статической неуравновешенности ротора

Итак, неуравновешенность – это состояние ротора, отличающееся таким распределением масс, которое во время вращения вызывает переменные нагрузки в опорах ротора. Мерой статической неуравновешенности является дисбаланс ротора D, мерой моментной неуравновешенности – главный вектор дисбаланса MD.

11.3.Приведение неуравновешенности ротора

кдвум плоскостям коррекции

Всякий ротор имеет множество дисбалансов, расположенных в различных плоскостях вращения. Выполняя уравновешивание ротора, можно было бы каждый из этих дисбалансов уменьшить до определённого значения. Для этого надо создавать в теле ротора дополнительные дисбалансы, направленные противоположно исходным дисбалансам, что обеспечивается постановкой дополнительных масс, которые называются корректирующими. Такой путь приводит к значительному увеличению массы ротора, поэтому применим другой метод.

Выберем в роторе три плоскости П, П1, П2 (рис. 11.2), перпендикулярные оси вращения. Подвижную систему координат OXYZ поместим в плоскость П.

368

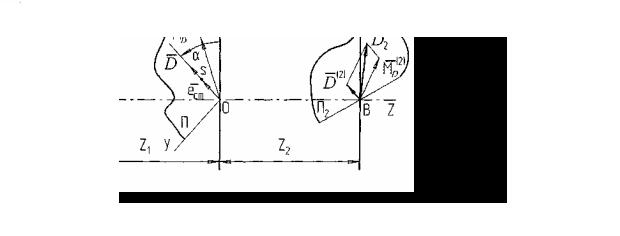
Рис. 11.2. Приведение неуравновешенности к двум плоскостям коррекции

В этой плоскости на линии главного вектора дисбалансов D находится центр масс ротораG , он составляет угол α с осью OX. Главный момент дисбалансов M D расположен в этой же плоскости П, он приложен в центре приведения, т.е. в начале координат, и составляет угол λ

сосью OX.

Сучётом (11.16), (11.17) находим тригонометрические функции углов α и λ :

где Z1, Z2 – аппликаты плоскостей коррекции с учётом их знаков.

В последнем выражении используютсяG G G модули дисбалансов, а не векторы, так как три дисбаланса D, D(1) , D( 2) параллельны.

С учётом (11.24), получаем

369

Знаменатель Z1 − Z2 представляет собой расстояние AB между плос-

смотреть с конца вектора M D , то момент пары должен быть положитель-

ным, т.е. направленным против часовой стрелки. Иначе говоря, вектор

Аналогично для второй плоскости коррекции (рис. 11.2, 11.3):

Рис. 11.3. Эквивалентные дисбалансы и дисбалансы корректирующих масс

370