Векторы этих сил F1 , F2 совпадают по направлению с дисбалансами D1 , D2 лишь при постоянной угловой скорости ротора. Эквивалентные дисбалансы в плоскостях коррекции оказывают на опоры ротора такое же силовое воздействие, что и векторы D, M D исходной неуравнове-
шенности. Геометрическая сумма дисбалансов D1 , D2 |
должна равняться |
вектору исходного дисбаланса D : |
|
D = D1 + D2 . |
(11.30) |
Моменты дисбалансов относительно начала координат системы OXYZ должны давать в сумме главный момент дисбалансов M D
Z1 D1 + Z2 D2 |
= M D |
(11.31) |
или в проекциях: |
|
|
−Z1 D1 y − Z2 D2 y = M Dx , |
(11.32) |
Z1 D1x + Z2 D2 x |
= M Dy . |
(11.33) |
При статической неуравновешенности нет вектора D , нет и векторов
M D(1) и M D(2) .
Остаётся вектор дисбаланса D и эквивалентные ему дисбалансы D1 , D2 в плоскостях коррекции. Эти три дисбаланса параллельны и направлены в одну сторону.
При моментной неуравновешенности нет вектора D и нет векторов D(1) , D( 2) . Остаётся вектор M D и эквивалентные ему пара дисбалансов M D(1) , M D(2) , которые равны по модулю и противоположны по направлению.
При динамической неуравновешенности есть оба вектора: D и M D . Эквивалентные дисбалансы D1 , D2 расположены в плоскостях коррекции произвольно (см. рис. 11.2).
11.4. Уравновешивание ротора
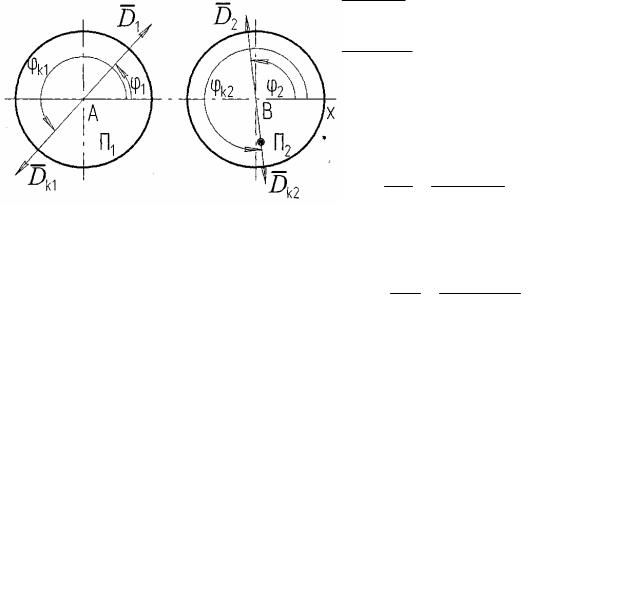
Любой из видов неуравновешенности можно устранить двумя корректирующими массами, расположенными в двух плоскостях коррекции, как показано на рис. 11.3. На этом рисунке изображены те же плоскости коррекции П, П1, П2, но в другой проекции. В плоскости П нет
371
дисбаланса D и момента дисбалансов M D , так как они представлены эквивалентными дисбалансами D1 , D2 в плоскостях коррекции П1, П2. Дисбалансы D1 , D2 составляют углы ϕ 1 ,ϕ 2 с осью OX. На продолжении ли-
ний дисбалансов с противоположной стороны установлены корректирующие массы mk1, mk2. Углы φk1, φk2 называются углами коррекции, они отличаются от углов φ1, φ2 на 180°, т.е.
φk1 = φ1 + 180°, φk2 = φ2 + 180°. |
(11.34) |
Корректирующие массы должны быть такой же величины и установлены на таких же эксцентриситетах, чтобы их дисбалансы по модулю были равны расчётным дисбалансам:
Dk1 = D1 , Dk 2 = D2 . |
(11.35) |
Выполнение условий (11.34), (11.35) позволяет уравновесить ротор динамически двумя корректирующими массами. Уравновешенный таким способом ротор не будет при вращении оказывать динамических воздействий на свои опоры как при постоянной, так и при переменной угловой скорости.
11.5. Балансировка роторов
Следует различать балансировку ротора при известном расположении неуравновешенных масс и случай, кода распределение масс неизвестно.
11.5.1.Балансировка ротора при известном распределении масс
Вкачестве примера рассмотрим балансировку ротора, содержащего пять дисков, на трёх из которых установлены дисбалансы, известные по величине и направлению (рис. 11.4). Расстояние между соседними дисками одинаково и равно a. В исходных данных укажем массы,
их эксцентриситеты и углы, которые составляют дисбалансы с осью Ax′, плоскости коррекции обозначим Пb, Гb.
Исходные данные для балансировки представлены ниже:
m1 |
e1 |
α1 |
m2 |
e2 |
α2 |
m3 |
e3 |
α3 |
|
|
|
|
|
|
|
|
|
50 |
60 |
0 |
50 |
60 |
90 |
50 |
90 |
120 |
|
|
|
|
|
|
|
|
|
Приведём решение двумя способами.
372

Первый способ
Находим проекции главного вектора дисбалансов (гмм):
|
|
|
|
Dx = m e cos α |
+ |
m e cosα |
+ |
m e cosα = |
3 |
|
|
|
|
|
|
1 |
1 |
|
1 |
2 |
2 |
2 |
3 |
3 |
|
|
|
|
|
= 50 60 cos 0° + 50 60 cos 90° + 50 60 cos120° = 1500. |
|
|
|
|
|
Dy = m e sin α |
+ |
m e sinα |
+ |
m e sinα = |
3 |
|
|
|
|
|
|
1 |
1 |
|
1 |
2 |
2 |
2 |
3 |
3 |
|
|
|
|
= 50 60 sin 0° + 50 60 sin 90° + 50 90 sin120° = 5598. |
Находим главный вектор дисбалансов: |
|
|
|
|
|
|
|
|
|
|
|
D = D2 |
+ D2 = |
15002 + 55982 = 5795, 4813. |
|
|
|
|
|
|
|
x |
|
y |
|
|
|
|
|
|
|
|
|
|
|
Тригонометрические функции угла α: |
|
|
|
|
|
|
|
|
|
|
Dx |
1500 |
|
|
|
|
|
|
Dy |
|
5598 |
|
|
cos α = |
|
|
= |
|
|
|
= 0, 2588; |
sinα = |
= |
|
|
|
|
= |
0, 9660 . |
|
|
|
|
|
|
|
|
|
|
D |
5795, 4813 |
|
|
|
|
D |
|
5795, 4813 |
Угол α находится в правой четверти круга, α = 75°. Систему координат X ′AY ′ совместим с первой плоскостью коррекции. Найдем координату Zs центра масс ротора в этой системе:
Zs |
= |
m1 (−a ) + m2 (−2a ) + m3 (−3a ) |
= |
−a (50 + 2 50 + 3 50) |
= −2a . |
m1 + m2 + m3 |
|
|
|
50 + 50 + 50 |
|
Следовательно, плоскость П (см. рис. 11.4) совпадает c плоскостью второго диска.
Рис. 11.4. Схема распределения неуравновешенных масс
Изобразим плоскости П, П1, П2 таким образом, чтобы углы на них откладывались безG искаженияG (рис. 11.5). С учётом (11.25), находим модули векторов D(1) , D(2) (гмм).
G |
(1) |
= −D |
Z2 |
= −5795, 4813 |
−2a |
= 2897,7406 . |
D |
|
|
|
|
Z1 − Z2 |
2a − (−2a ) |
Рис. 11.5. К расчёту эквивалентных дисбалансов
|
|
|
|
G |
( 2) |
= −D |
|
|
Z1 |
= |
5795, 4813 |
2a |
|
|
|
= 2897, 7406 . |
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z1 − Z2 |
2a − (−2a ) |
|
|
|
|
Вычислим центробежные моменты: |
|
|
|
|
|
|
|
|
J |
xy |
= am e cos α |
|
− |
am e cosα |
= |
a (50 |
|
60 cos°0− |
50 |
60 cos120° =) |
4500a. |
|
1 |
1 |
|
|
|
1 |
|
|
3 |
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J yz |
|
= −am3e3 sin α 3= − a 50 |
60 sin120° = − 2598a. |
|
|
|
|
Находим модуль главного момента дисбалансов: |
|
|
|
|
|
|
|
|
M D |
= |
|
J xy2 + J yz2 = a |
45002 + 25982 |
= 5196,1143a . |
|
|
|
|
Тригонометрические функции угла λ : |
|
|
|
|
|
|
|
|
|
|
|
J yz |
|
|
|
|
|
|
|
−2598a |
|
|
|
|
|
|
|
|
|
J xy |
4500a |
|
|
cos λ = − |
|
|
|
= − |
|
|
|
|
|
|
|
|
|
|
|
|
= |
0,500, |
sinλ = − |
|
= − |
|
= |
0,866 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M D |
|
|
|
|
|
5196,1143a |
|
|
|
|
|
|
|
|
|
M D |
5196,1143a |
|
|
|
Угол λ находится в первой четверти круга, λ = 60° . |
|
|
|
|
Моменты дисбалансов в плоскостях коррекции (гмм): |
|
|
|
|
|
|
|
|
|
|
|
|
|
M D(1) |
|
= |
|
M D( 2) |
|
= |
M D |
= |
5196,1143a |
= 1299 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4a |
|
|
4a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Уголλ1 впервойплоскостикоррекции: λ1 = λ+ 270° = 60° + 270° = 330°. Аналогично для второй плоскости: λ2 = λ + 90° = 60° + 90° = 150°. Теперь проектируем найденные дисбалансы на оси координат:
Dx(1) |
= Dx( 2) = D(1) cos α = |
2897, 7406 |
cos 75° = |
750 , |
Dy(1) |
= Dy( 2) = D( 2) sin α = |
2897,7406 |
sin 75° = |
2799 , |
M Dx(1) = −M Dx(2) = M D(1) cos λ 1= 1299 cos 330° = 1125,
M Dy(1) = −M Dy(2) = M D(1) sin λ 1= 1299 sin 330° = − 649,5 .
374
Проекции эквивалентных дисбалансов в плоскостях коррекции:
D |
= D(1) |
|
+ M (1) = 750 +1125 = 1875 , |
|
1x |
x |
|
|
|
Dx |
|
D |
= D(2) |
|
+ M |
( 2) = 750 −1125 = −375 , |
|
2 x |
x |
|
|
|
Dx |
|
D |
= D(1) |
+ M |
(1) |
= 2799 − 649,5 = 2149,5 , |
1 y |
|
y |
|
|
|
Dy |
|
|
D |
= D( 2) |
+ M |
( 2) = 2799 + 649,5 = 3448,5. |
2 y |
|
y |
|
|
|
Dy |
|
|
Модули дисбалансов (гмм): |
|
|
D = |
D2 + D2 |
|
= |
|
18752 + 2149,52 |
= 2852, 363, |
1 |
1x |
1 y |
|
|
|
|
D = D2 |
+ D2 |
|
= |
(−375)2 + 3448,52 |
= 3468,8293 . |
2 |
2 x |
2 y |
|
|
|
|
|
Тригонометрические функции углов отклонения дисбалансов от оси OX:
|
|
|
D |
1875 |
|
|
|
|
D1 y |
2149,5 |
|
|
|
cos ϕ = |
1x |
= |
|
|
= 0, 657, |
sinϕ |
= |
= |
|
|
|
= |
|
0, 750 . |
|
|
|
|
|
|
|
|
|
|
1 |
|
D1 |
2852, 363 |
|
1 |
D1 |
2852, 363 |
|
|
|
|
|
|
|
|
|
Угол ϕ |
1 находится в первой четверти круга, ϕ |
1 = 48°54 ' (рис. 11.6): |
|
|
D |
−375 |
|
|
|
|
|
D2 y |
3448,5 |
|
|
cos ϕ = |
|
|
2 x |
= |
|
|
= − 0,108, |
sinϕ |
= |
|
= |
|
|
|
|
= |
0, 994 . |
|
|
|
|
|
|
|
|
|
2 |
|
D2 3468,8293 |
|
2 |
|
D1 |
3468,8293 |
|
|
|
|
|
|
|
Угол ϕ |
2 |
находится во второй четверти круга, |
ϕ 2 = 96°12 ' . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.6. Эквивалентные дисбалансы и дисбалансы корректирующих масс

Проведём проверку расчёта. Для этого распишем выражение (11.30) в проекциях:
Dx = D1x + D2 x = 1875 − 375 = 1500 ,
Dy = D1 y + D2 y = 2149 − 3448 = 5598 .
Из выражений (11.32), (11.33) получаем
G |
G |
G |
G |
G |
|
−Z1 |
D1 y − Z2 D2 y |
= M Dx = −J zy или −2a 2149,5 − (−2a ) 3448,5 = 2598a . |
|
G |
G |
G |
G |
G |
|
Z1 D1x |
+ Z2 D2 x = M Dy = J xz или 2a 1875 − 2a (−375) = 4500a . |
Обе проверки подтверждают правильность расчёта. Углы коррекции |
ϕ k1 , ϕ |
k 2 |
отличаются от углов ϕ 1 , ϕ 2 на 180°. |
|
|
|
ϕ |
k1 = ϕ |
1 +180° = 48°54 '+180° = 228°54 ' , |
|
|
|
ϕ |
k 2 = ϕ |
2 +180° = 96°12 '+180° = 276°12 ' . |
Далее задаёмся корректирующими массами TK1, TK2 и находим их эксцентриситеты (мм):
e |
= |
DK1 |
= |
2852,363 |
= 71,3, e |
K 2 |
= |
DK 2 |
= |
3468,8293 |
= 57,8 |
|
|
|
|
K1 |
|
mK1 |
40 |
|
|
mK 2 |
60 |
|
|
|
|
|
|
|
Приведём таблицу вариантов для расчётной работы.
№ варианта |
m1 |
e1 |
α1 |
m2 |
e2 |
α2 |
m3 |
e3 |
α3 |
1 |
30 |
60 |
0 |
50 |
60 |
90 |
50 |
60 |
120 |
2 |
60 |
50 |
0 |
50 |
60 |
90 |
40 |
50 |
150 |
3 |
40 |
60 |
0 |
40 |
50 |
120 |
50 |
50 |
210 |
4 |
60 |
40 |
0 |
50 |
40 |
120 |
60 |
50 |
210 |
5 |
50 |
40 |
0 |
60 |
40 |
90 |
40 |
60 |
120 |
6 |
30 |
50 |
0 |
30 |
70 |
240 |
40 |
60 |
120 |
7 |
40 |
60 |
0 |
30 |
50 |
240 |
50 |
60 |
120 |
8 |
60 |
40 |
0 |
50 |
50 |
120 |
40 |
60 |
90 |
9 |
40 |
50 |
0 |
60 |
40 |
90 |
50 |
60 |
120 |
10 |
50 |
60 |
0 |
40 |
50 |
120 |
60 |
40 |
270 |
11 |
30 |
70 |
0 |
40 |
80 |
90 |
60 |
40 |
120 |
12 |
60 |
40 |
0 |
50 |
40 |
120 |
50 |
40 |
270 |
13 |
40 |
50 |
0 |
40 |
60 |
150 |
40 |
50 |
240 |
14 |
60 |
40 |
0 |
50 |
40 |
120 |
40 |
50 |
240 |
15 |
50 |
60 |
0 |
40 |
60 |
150 |
50 |
60 |
210 |
Второй способ
По этому способу разносим дисбалансы неуравновешенных масс в плоскости коррекции, используя формулы (11.25). Дисбаланс (гмм) на первом диске (рис. 11.4):
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
Z2 |
= −50 60 |
|
−3a |
|
|
|
|
m1e1 = −m2e2 |
|
|
|
|
|
|
|
|
|
|
|
|
= 2250 , |
Z1 − Z2 |
|
|
a − (−3a ) |
|
( 2) |
= −m1e1 |
Z1 |
|
|
= 50 60 |
|
|
|
a |
|
= 750 . |
m1e1 |
|
|
|
|
|
|
|
|
|
|
|
|
Z1 − Z2 |
a − (−3a ) |
|
Дисбалансы (гмм) на втором диске: |
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
|
|
|
|
|
|
|
Z2 |
|
|
|
|
|
|
|
|
−2a |
|
|
|
|
m1e2 = −m2e2 |
|
|
|
|
= −50 60 |
|
|
|
|
= 1500 , |
Z1 − Z2 |
2a − (−2a ) |
( 2) |
= −m2e2 |
|
|
|
|
Z1 |
|
= 50 60 |
|
|
|
|
|
2a |
|
= 1500 . |
m1e2 |
|
|
|
|
|
|
|
|
|
|
Z1 − Z2 |
|
2a − (−2a ) |
Дисбалансы (гмм) на третьем диске: |
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
= −m3e3 |
|
|
Z2 |
|
|
= −50 60 |
|
|
−a |
|
|
= 750 , |
m3e3 |
|
|
|
|
|
|
|
Z1 − Z2 |
|
|
3a − (−a ) |
(2) |
|
= −m3e3 |
|
Z1 |
|
|
= 50 60 |
|
|
|
|
3a |
= 2250 . |
m3e3 |
|
|
|
|
|
|
|
|
Z1 − Z2 |
|
|
|
3a − (−a ) |
Находим проекции дисбалансов в плоскостях коррекции (гмм):
D |
= m e(1) |
cos α |
+ |
m e(1) |
cosα |
+ |
m e(1) |
cosα = |
3 |
1x |
1 1 |
|
1 |
2 2 |
|
2 |
3 3 |
|
= 2250 cos 0° +1500 cos 90° + 750 cos120° = 1875,
D |
= m e(1) |
cos α |
+ |
m e(2) cosα |
+ |
m e( 2) cosα = |
3 |
2 x |
1 1 |
|
1 |
2 2 |
2 |
3 3 |
= 750 cos 0° +1500 cos 90° + 2250 cos120° = −375,
D |
= m e(1) |
sin α |
+ |
m e(1) |
sinα |
+ |
m e(1) |
sinα = |
3 |
1 y |
1 1 |
|
1 |
2 2 |
|
2 |
3 3 |
|
= 2250 sin 0° +1500 sin 90° + 750 sin120° = 2149,5,
D |
= m e( |
2) sin α |
+ |
m e( 2) sinα |
+ |
m e( 2) sinα = |
3 |
2 y |
1 1 |
|
1 |
2 2 |
2 |
3 3 |
= 750 sin 0° +1500 sin 90° + 2250 sin120° = 3448,5.

Находим модули дисбалансов в плоскостях коррекции (гмм):
D = |
D2 |
+ D2 |
|
= |
18752 + 2149,52 |
= 2852, 363, |
1 |
|
1x |
1 y |
|
|
|
D = |
D2 |
+ D2 |
= |
(−375)2 + 3448,52 |
= 3468,8293 . |
2 |
2 x |
|
2 y |
|
|
|
|
Тригонометрические функции углов отклонения дисбалансов от оси OX:
|
|
|
|
D |
1875 |
|
|
|
|
D1 y |
2149,5 |
|
|
|
cos ϕ |
= |
|
|
1x |
= |
|
|
= 0, 657, |
sinϕ |
= |
= |
|
= |
|
0, 750 , |
|
|
|
|
|
|
|
|
1 |
|
D1 |
2852, 363 |
|
1 |
D1 |
2852, 363 |
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
−375 |
|
|
|
|
D2 y |
3448,5 |
|
|
cos ϕ = |
|
2 x |
= |
|
|
= − 0,108, |
sinϕ |
= |
= |
|
|
= |
0, 994 . |
|
|
|
|
|
|
2 |
|
D2 |
3468,8293 |
|
|
2 |
D1 |
3468,8293 |
|
|
|
|
|
|
|
Угол ϕ 1 находится в первой четверти круга, ϕ |
1 = 48°54 ' . |
|
|
Угол ϕ |
|
2 находится во второй четверти круга, |
ϕ 2 = 96°12 ' . |
|
Следовательно, по второму способу сразу получены эквивалентные дисбалансы в плоскостях коррекции, совпадающие с дисбалансами, найденными по первому способу.
Однако по второму способу не выявляются раздельно статическая и моментная неуравновешенности, хотя различать их можно из следующих условий:
1.Если эквивалентные дисбалансы параллельны и направлены в одну сторону, это соответствует статической неуравновешенности.
2.Если эквивалентные дисбалансы образуют пару, это соответствует моментной неуравновешенности.
3.Произвольное расположение дисбалансов соответствует динамической неуравновешенности.
11.5.2.Балансировка ротора при неизвестном распределении масс
Неуравновешенность ротора может возникать по разным причинам: из-за неоднородности материала, неточности изготовления и сборки деталей ротора и машины в целом, деформации деталей ротора во время его эксплуатации, износа элементов опорных кинематических пар и т.п. Эти факторы трудно учесть и рассчитать при конструировании ротора, поэтому для устранения неуравновешенности применяют специальное оборудование – балансировочные станки.

Основные сведения о балансировочном станке резонансного типа
Рассмотрим расчётную модель простейших балансировочных станков резонансного типа (рис. 11.7).
Рис. 11.7. Расчётная модель балансировочного станка резонансного типа
Ротор 3 с заранее предусмотренными плоскостями коррекции 1 и 2 установлен в раме 4, которая может поворачиваться относительно шарнира O. На расстоянии λ1 от этой точки O рама опирается на пружину 7, на расстоянии λ2 установлен индикатор часового типа 5. Позициями 5 и 8
|
на модели |
показаны |
элементы |
конструкционного демпфирования |
|
в индикаторе, пружина в опоре O. В станке применяется механическое |
|
разделение дисбаланса двух плоскостей коррекции. |
G |
|
На виде |
А модели |
показаны |
эквивалентные дисбалансы |
|
D1 , D2 |
в плоскостях коррекции и силы F1 , F2 , которые развивают дисбалансы при вращении с постоянной частотой ω. Система O1,2, x0, y0 неподвижна. Угол, который составляет дисбаланс D1 с осью x0, обозначен ωt, где t – параметр времени.
Механическое разделение дисбалансов заключается в том, что один из
G G
них (в данном случае D2 ) установлен так, что линия действия силы F2 про-
ходит через точку качания рамы. Плоскость коррекции 1 называется кон-
G
тролируемой, плоскость 2 – исключаемой. Проекция силы F на вертикаль
G 1
F1x = F1 cos ω t действует на плечо z относительно оси качания рамы. Мо-
мент этой силы F1Z cos ω t вызывает периодическое угловое отклонение ра-

мы, амплитуда которого является |
мерой дисбаланса в контролируемой |
плоскости коррекции. Момент силы |
G |
изменяется по гармоническому за- |
F1 |
кону с частотой ω, равной угловой скорости ротора. По мере убывания угловой скорости ротора заG счёт трения уменьшается и частота изменения возмущающего момента F1Z cos ω t . Когда частота СО станет близка к собственной частоте колебаний K1, возникает состояние резонанса. Из теории колебаний известно, что при резонансе амплитуда вынужденных колебаний может считаться пропорциональной амплитуде возмущающего фактора.
Описание процесса балансировки контролируемой плоскости коррекций
Предложено много методов одноплоскостной балансировки ротора. Рассмотрим метод двух пробных кусков. Придаём ротору быстрое вращение с помощью специального привода. После отключения привода позволяем ротору свободно вращаться в режиме выбега. При достижении частоты ωрез замеряем амплитуду A1, вызванную эквивалентным дисбалансом в контролируемой плоскости коррекции. Амплитуда и дисбаланс связаны между собой масштабным коэффициентом дисбаланса A1 = kω 1D1 . Установим в контролируемой плоскости пробную массу с известным дисбалансом Dn и произведём первый пробный пуск. Замеренная амплитуда A1 будет пропорциональна суммарному дисбалансу (рис. 11.8):
|
A2 = kω 1D2 , |
(11.36) |
|
|
D2 = |
G |
G |
|
|
где |
D1 |
+ Dn . |
(11.37) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 11.8. Метод одноплоскостной балансировки ротора