
472
.pdf2.3.27. Найти значение , при котором прямая |
x 2 |
y 7 |
z 6 |
и плоскость |
||||||||||||
4 |
3 |
|||||||||||||||
x 3y 2z 4 0 параллельны. |
|
|
|
|
|
|
||||||||||
|
x 3 |
|
y 1 |
|
|
|
||||||||||
2.3.28. Найти значение p , при котором прямые |
|
|
z и |
|
||||||||||||
|
2 p |
3p |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x 2 |
|
y 7 |
|
z 5 |
параллельны. |
|
|
|
|
|
|
|
|
|
|
4 |
12 |
|
|
|
|
|
|
|
|
|
|
|||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|||||
2.3.29.Найти значение b , при котором плоскости 7x y bz 3 0 иb 1 x 2y z 4 0 взаимно перпендикулярны.
2.3.30.Найти значение t , при котором плоскости tx (t 2)y z 5 0 и 6x 2y (t 1)z 8 0 параллельны.
49
Оглавление |
|
|
Оглавление............................................................................................ |
1 |
|
3. Кривые второго порядка................................................................ |
2 |
|
3.1 |
Окружность.................................................................................. |
2 |
3.2 |
Эллипс и его свойства................................................................ |
3 |
3.3 |
Гипербола и ее свойства............................................................. |
9 |
3.4 |
Парабола и ее свойства............................................................. |
17 |
3.5 |
Формулы преобразования координат при параллельном |
|
переносе координатных осей......................................................... |
19 |
|
3.6 |
Уравнения кривых второго порядка с осями симметрии, |
|
параллельными координатным осям.......................................... |
20 |
|
3.7 |
Формулы преобразования координат при повороте |
|
координатных осей.......................................................................... |
22 |
|
3.8 |
Общее уравнение кривой второго порядка. Приведение к |
|
каноническому виду ....................................................................... |
22 |
|
3.9 |
Инварианты кривых второго порядка ................................. |
26 |
Задачи для самостоятельного решения....................................... |
27 |
|
1

3.Кривые второго порядка
3.1Окружность
Определение. Окружностью называется геометрическое место точек на плоскости, равноудаленных от некоторой фиксированной точки плоскости, называемой центром окружности.
Расстояние от центра окружности до любой ее точки называется радиусом окружности (рис. 3.1).
Получим уравнение окружности радиуса R с центром в точке М(a;b). Обозначим координаты произвольной точки на окружности N(x;y).
Вычислим расстояние от центра до этой точки как длину соответствующего
вектора MN и приравняем его к значению радиуса R:
 (x - a)2 (y b)2 R .
(x - a)2 (y b)2 R .
Возведем обе части полученного равенства в квадрат, получим: |
|
|||
(x – a)2 + (y – b)2 = R2 - |
y |
|
||
уравнение окружности с |
|
|||
N(x;y) |
|
|||
центром в точке с координатами |
|
|||
|
|
|||
(a; b) радиуса R. |
|
R |
|
|
Пример. |
Найти |
координаты |
M(a;b) |
|
|
|
|||
центра и радиус окружности, |
|
|
||
если ее уравнение задано в виде: |
0 |
x |
||
2x2 + 2y2 – 8x + 5y – 4 = 0. |
||||
Решение. |
Для |
нахождения |
Рис. 3.1 |
|
|
|
|||
координат |
центра |
и радиуса |
|
|
окружности данное уравнение необходимо привести к виду, указанному выше. Для этого выделим полные квадраты:
x2 + y2 – 4x + 2,5y – 2 = 0
x2 – 4x + 4 –4 + y2 + 2,5y + 25/16 – 25/16 – 2 = 0 (x – 2)2 + (y + 5/4)2 – 25/16 – 6 = 0
(x – 2)2 + (y + 5/4)2 = 121/16
Отсюда находим О(2; -5/4); R = 11/4.
Пример. Найти уравнение траектории точки, которая перемещаясь по плоскости xOy, остаётся в два раза дальше от точки A ( 3,0), чем от начала
координат (рис. 3.2 )
2

Решение. Текущую точку на искомой траектории обозначим M (x ,y ). В |
|||||||||||||||||
силу |
условия задачи |
|
|
|
|
|
2 |
|
. |
|
|
|
x i y j; |
||||
|
|
|
A M |
|
O M |
A M (x 3)i y j, O M |
|||||||||||
|
|
|
(x 3)2 y 2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 y 2 , |
значит |
(x 3)2 |
y 2 2 |
x 2 y 2 . |
||||||||||
|
A M |
|
O M |
|
|||||||||||||
Возведя |
в квадрат, |
получим |
|
(x 3)2 |
y 2 4x 2 |
4y 2 , |
откуда |
следует |
|||||||||
x 2 6x 9 y 2 4x 2 4y 2 . Имеем 3x 2 3y 2 6x 9. |
|
|
|||||||||||||||
|
Упрощаем: x 2 y 2 2x 3. |
|
|
|
|
|
|
|
|||||||||
|
Выделяем полный квадрат: x 2 2x 1 y 2 3 1. |
|
|
|
|||||||||||||
Окончательно имеем: (x 1)2 |
y 2 22 . Получили окружность (рис. 3.3 ) |
||||||||||||||||
Рис. 3.2 |
|
Рис. 3.3 |
|
|
|
3.2 Эллипс и его свойства
Определение. Эллипсом называется множество точек на плоскости,
сумма расстояний от которых до двух данных точек, называемых фокусами, есть величина постоянная (равная 2a , a 0), большая, чем
расстояние между фокусами.
(ЭЛЛИПС)
Принимая во внимание определение эллипса, выведем его уравнение. Если определённым образом выбрать систему координат, то можно получить простейшую форму уравнения эллипса, которая называется каноническим уравнением (рис. 3.4). Итак, проведём ось Ox через фокусы от фокуса F1 к
фокусу F2 .

Начало координат возьмём в середине отрезка F1F2 . Если расстояние между фокусами обозначить через 2c (c 0), то очевидно, что фокусы
имеют координаты F1( c ,0), F2(c ,0).
Ось Oy направим так, чтобы система xOy была бы правой. Пусть точка
M (x ,y ) принадлежит эллипсу, векторы r1 |
и r2 называются её фокальными |
|||||||||
радиус-векторами. |
|
|
r1 |
|
|
|
r2 |
|
2a (a 0, a c ). |
|
В силу определения эллипса |
|
|
|
|
|
|||||
|
|
|
|
|||||||
Отсюда следует: |
|
|
|
|
|
|
|
|
|
|
(x c )2 y 2 (x c )2 y 2 2a => |
(x c )2 y 2 2a (x c )2 y 2 |
|||||||||
=> (x c )2 y 2 4a 2 4a |
(x c )2 y 2 (x c )2 y 2 => |
|||||||||
=> x 2 2xc c 2 4a 2 4a |
(x c )2 y 2 x 2 2xc c 2 y 2 => |
|||||||||
=> 4xc 4a 2 4a |
(x c )2 y 2 => xc a 2 a |
(x c )2 y 2 => |
|||
=> x 2c 2 2a 2xc a 4 a 2x 2 2a 2xc a 2c 2 a 2y => |
|||||
=>(a 2 c 2) x 2 a 2y 2 a 2 (a 2 c 2). |
|
|
|
||
Обозначим a 2 c 2 |
b2 , тогда из предыдущего следует: |
||||
|
x 2 |
|
y 2 |
1. |
|
|
a 2 |
b2 |
|
||
|
|
|
|
||
Это уравнение называется каноническим уравнением эллипса. Эллипс пересекает координатные оси в точках A1( a ,0), A2(a ,0), B 2(0,b) и
B 2(0, b), которые называются вершинами эллипса. Отрезки A1A2 и B1B 2 ,
равные 2a и 2b соответственно, называются большой и малой осями эллипса, a и b - большой и малой полуосями. Эллипс симметричен относительно координатных осей и относительно начала координат.
Теорема. Фокусное расстояние и полуоси эллипса связаны соотношением:
a2 = b2 + c2.
Доказательство. В случае, если точка М находится на пересечении эллипса
с вертикальной осью, r1 + r2 = 2 b2 c2 (по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, r1 + r2 = a – c + a + c. Т.к. по определению сумма r1 + r2 – постоянная величина, то, приравнивая, получаем:
b2 c2 (по теореме Пифагора). В случае, если точка М находится на пересечении эллипса с горизонтальной осью, r1 + r2 = a – c + a + c. Т.к. по определению сумма r1 + r2 – постоянная величина, то, приравнивая, получаем:
a2 = b2 + c2 r1 + r2 = 2a.
4

Определение. Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется
эксцентриситетом.
ε = с/a.
Т.к. с < a, то ε < 1.
Определение. Величина k = b/a называется коэффициентом сжатия
эллипса, а величина 1 – k = (a – b)/a называется сжатием эллипса.
Коэффициент сжатия и эксцентриситет связаны соотношением: k2 = 1 – ε2.
Если a = b (c = 0, ε = 0, фокусы сливаются), то эллипс превращается в окружность.
Если |
для точки М(х1, |
у1) выполняется |
условие: |
x2 |
|
y 2 |
1, то |
она |
|||||
1 |
|
1 |
|||||||||||
a2 |
b2 |
||||||||||||
|
|
|
x2 |
|
y 2 |
|
|
|
|
||||
находится |
внутри эллипса, |
а если |
|
1, то точка |
находится |
вне |
|||||||
1 |
|
1 |
|
||||||||||
a2 |
b2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||
эллипса.
Теорема. Для произвольной точки М(х, у), принадлежащей эллипсу верны соотношения r1 = a – ε x, r2 = a + ε x.
Доказательство. Выше было показано, что r1 + r2 = 2a. Кроме того, из геометрических соображений можно записать:
r1  (x c)2 y 2 r2
(x c)2 y 2 r2  (x c)2 y 2
(x c)2 y 2
(x c)2 y 2 (x c)2 y 2 2a
После возведения в квадрат и приведения подобных слагаемых:
(x c)2 y2 4a2 4a (x c)2 y2 (x c)2 y2
4cx 4a2 4a (x c)2 y2
 (x c)2 y a ac x a x.
(x c)2 y a ac x a x.
Аналогично доказывается, что r2 = a + εx. Теорема доказана.
Сэллипсом связаны две прямые, называемые директрисами. Их уравнения:
x= a/ε; x = -a/ε (рис. 3.5).
Теорема. Если r — расстояние от произвольной точки эллипса до какогонибудь фокуса, d — расстояние от этой же точки до соответствующей этому фокусу директрисы, то отношение r/d есть постоянная величина, равная
эксцентриситету эллипсаdr .
5

|
|
|
|
|
Рис. 3.5 |
|
|
|
|
|
|
||||
Если величины полуосей эллипса связаны соотношением |
а < b, то |
||||||
уравнение |
x 2 |
y 2 |
1 |
определяет эллипс, большая ось которого 2b |
лежит на |
||
a 2 |
b2 |
||||||
оси Оу, а малая ось 2a — на оси Ох (рис. 3.6). Фокусы такого эллипса
находятся в точках |
F (0,c) |
и |
F (0, c), где c |
b2 a2 . |
|
1 |
|
2 |
|
Рис. 3.6
Пример. Составить уравнение прямой, проходящей через левый фокус и
нижнюю вершину эллипса, заданного уравнением: x2 y 2 1. 25 16
Решение.
1)Координаты нижней вершины: x = 0; y2 = 16; y = -4.
2)Координаты левого фокуса: c2 = a2 – b2 = 25 – 16 = 9; c = 3; F2(-3; 0).
3)Уравнение прямой, проходящей через две точки:
x 0 |
|
y |
4 |
; |
x |
|
y 4 |
; |
4x 3y 12; |
4x 3y 12 0. |
|
3 0 |
0 |
4 |
3 |
4 |
|||||||
|
|
|
|
|
|
Пример. Составить уравнение эллипса, если его фокусы F1(0; 0), F2(1; 1), большая ось равна 2.
6

Решение. Уравнение |
эллипса имеет вид: |
x2 |
|
y2 |
1. Расстояние между |
|||||||||||||
a2 |
b2 |
|||||||||||||||||
фокусами: |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2c = |
|
(1 0)2 (1 0)2 |
|
2 , таким образом, a2 – b2 = c2 = ½ |
y |
|||||||||||||
по условию 2а = 2, следовательно а = 1, b = |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|||||||||||||
|
a2 c2 1 1/2 2 /2. |
|
|
|
|
|
|
|
||||||||||
Таким образом, уравнение эллипса имеет вид |
|
|
|
|
|
|
||||||||||||
|
x2 |
|
|
y 2 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пример. Найти сторону квадрата, вписанного |
|
|
|
|
|
|
|
|||||||||||
в данный эллипс |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
x 2 |
|
y 2 |
1. (рис. 3.7 ) |
|
|
|
|
|
Рис. 3.7 |
|
|||
|
|
|
4 |
2 |
|
2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||
Решение. В силу симметрии эллипса вершины квадрата, вписанного в эллипс, имеют координаты:M 1(m ,m ),M 2( m ,m ),M 3( m ,m ), M 4(m , m ), (m 0). Искомая длина стороны квадрата d 2m . Координаты
точки M 1 удовлетворяют уравнению эллипса, потому имеем
m422 m322 1 => 32m 2 42m 2 32 92 => m 2,4.
Итак, длина стороны квадрата d 4,8.
Замечание 1. Форму эллипса можно охарактеризовать с помощью
эксцентриситета ac (0 1). Чем больше эксцентриситет, тем более вытянутую форму вдоль оси Ox имеет кривая.
7

Замечание 2. Определение эллипса как кривой, описываемой точкой М так, что сумма расстояний этой точки до двух неподвижных точек F1 и F2 остается неизменной, может быть использовано при построении эллипса при отсутствии специальных чертежных инструментов. Возьмем нить, концы ее привяжем к двум булавкам и воткнем эти булавки в
лист бумаги, оставляя сначала нить ненатянутой. Если оттянуть теперь нить с помощью вертикально поставленного карандаша и затем передвигать карандаш, слегка придавливая его к бумаге и следя за тем, чтобы нить была натянутой (рис. 3.8), то острие М карандаша опишет кривую, являющуюся эллипсом. Чтобы получить полный эллипс, придется перекинуть нить на другую сторону от булавок, после того как будет описана одна половина эллипса. Очевидно, что сумма расстояний от острия М карандаша до фокусов (булавочных проколов) F1 и F2 остаётся неизменной во все время движения; эта сумма равна длине нити.
(ЭЛЛИПС)
Замечание 3. Слово “фокус” в переводе с латинского означает «очаг», «огонь»; оно оправдывается следующим замечательным свойством эллипса. Если изогнуть узкую полоску хорошо отполированного металла по дуге
|
эллипса и поместить точечный |
|
источник света («огонь») в одном |
|
фокусе, то лучи света, отразившись от |
|
полоски, соберутся в другом фокусе; |
|
поэтому и во втором фокусе будет |
|
также виден «огонь» - изображение |
Рис. 3.9 |
первого (рис. 3.9). |
|
Замечание 4. И. Кеплер (1571-1630), предложивший новую модель мира, доказал, что каждая планета Солнечной системы движется по траектории эллипса, в одном из фокусов которого находится Солнце (рис. 3.10).
8
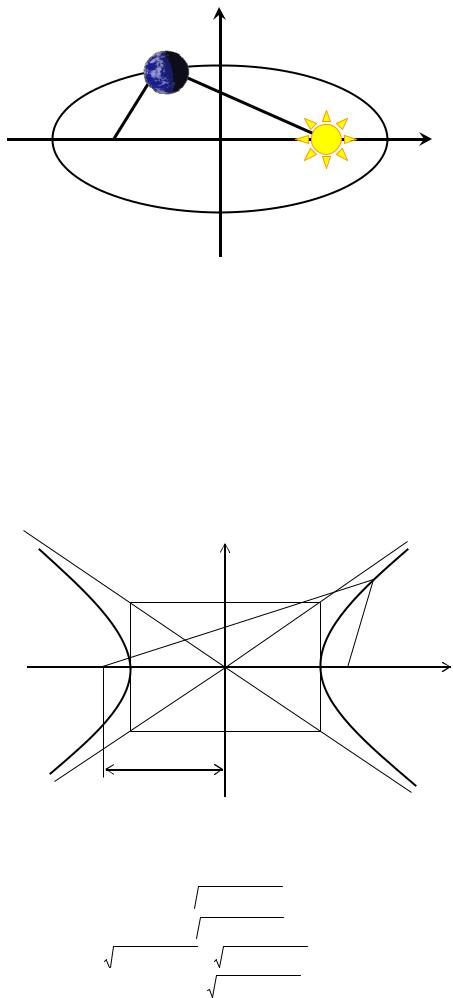
y
F1 |
F2 |
x |
Рис. 3.10
3.3 Гипербола и ее свойства
Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная (равная 2a, a>0), меньшая расстояния между фокусами.
(ГИПЕРБОЛА) y
M(x, y)
|
(0;b) |
|
r1 |
|
r2 |
|
x |
(-a;0) |
(a;0) |
F1 |
F2 |
|
(0;-b) |
c
Рис. 3.11
По определению r1 – r2 = 2a. F1, F2 – фокусы гиперболы. F1F2 = 2c. Выберем на гиперболе произвольную точку М(х, у) (рис.3.11). Тогда:
r1  (x c)2 y 2 r2
(x c)2 y 2 r2  (x c)2 y 2
(x c)2 y 2
(x c)2 y2 (x c)2 y2 2a
(x c)2 y 2 4a2 4a (x c)2 y 2 (x c)2 y 2
9
