472

C

N

Записать уравнение плоскости – значит связать некоторым равенством координаты произвольной точки плоскости. Поэтому возьмем произвольную точку M x; y;z на искомой плоскости:

C M

N

Определим вектор CM :

C M

N

Найдем координаты вектора CM :

CM x 2;y 3;z ( 5) x 2; y 3;z 5 .

Векторы CM и N перпендикулярны, следовательно, их скалярное произведение равно 0:

3 x 2 2 y 5 z 5 0.

После преобразований получаем:

19

p

D

l

Записать уравнение плоскости – значит связать некоторым равенством координаты произвольной точки плоскости. Поэтому возьмем произвольную точку M x; y;z на искомой плоскости:

p

D

l

M

Определим вектор DM :

p

D

l

M

21

Найдем координаты вектора DM :

DM x 2; y ( 4);z 3 x 2; y 4;z 3 .

Векторы DM и p перпендикулярны, следовательно, их скалярное произведение равно 0:

5 x 2 2 y 4 0 z 3 0 или 5x 2y 2 0.

Последнее уравнение является общим уравнением искомой плоскости.

§2.8. Нормальное уравнение плоскости

(уравнение плоскости, находящейся на расстоянии p от начала координат, нормаль к которой составляет углы , β и γ с

положительными направлениями осей координат соответственно)

Сделаем рисунок. Расстояние от начала координат до плоскости определяется длиной перпендикуляра OP , проведенного из начала координат к плоскости. Нормаль к плоскости – это перпендикуляр к плоскости.

z

P

e

x

Записать уравнение плоскости – значит связать некоторым равенством координаты произвольной точки плоскости. Поэтому возьмем произвольную точку M x; y;z на искомой плоскости:

22

z

x

Определим векторы OM и единичный вектор e , сонаправленный вектору OP :

z

x

Найдем координаты этих векторов:

часть, окончательно получим:

x cos y cos z cos p 0.

23

ВАЖНО:

1)Полученное уравнение называется нормальным уравнением плоскости.

2)В нормальном уравнении плоскости свободный член всегда неположителен. Модуль свободного члена в нормальном уравнении плоскости определят расстояние от плоскости до начала координат.

3)В нормальном уравнении плоскости коэффициенты при x , y и z определяют координаты единичного нормального вектора плоскости. Сумма квадратов этих коэффициентов равна 1.

§2.9. Приведение общего уравнения плоскости к нормальному виду

Нормальное уравнение плоскости – это частный случай общего уравнения плоскости. Если для коэффициентов общего уравнения плоскости выполняются условия 2), 3) из предыдущего параграфа, то уравнение является нормальным.

Пример. Выбрать из предложенных уравнений нормальные:

а) 3x 2y 5z 3 0;

Решение. В нормальном уравнении плоскости свободный член должен быть неположителен, поэтому уравнение б) не является нормальным, уравнение б) – общее уравнение плоскости.

Сумма квадратов коэффициентов при переменных в нормальном уравнении плоскости равна единице.

является нормальным. Уравнение а) – общее уравнение плоскости.

следовательно, уравнение является нормальным.

Как свести общее уравнение плоскости к нормальному? Мы можем преобразовать уравнение, умножив его на некоторое число так, чтобы новое уравнение удовлетворяло условиям нормальности. Пусть дано общее уравнение плоскости:

Ax By Cz D 0.

Умножим его на некоторое число T :

ATx BTy CTz DT 0.

24

Полученное уравнение будет нормальным, если DT 0, т.е. знак числа T

знаком, противоположным знаку свободного члена.

Пример. Привести уравнение плоскости 3x 2y 3z 1 0 к нормальному

виду.

Решение. Дано общее уравнение плоскости. Чтобы привести его к нормальному виду, необходимо обе его части разделить на корень квадратный из суммы квадратов коэффициентов при переменных, взятый со знаком «–» (противоположным знаку свободного члена +1).

Полученное уравнение является нормальным уравнением плоскости.

§2.10. Расстояние от точки до плоскости

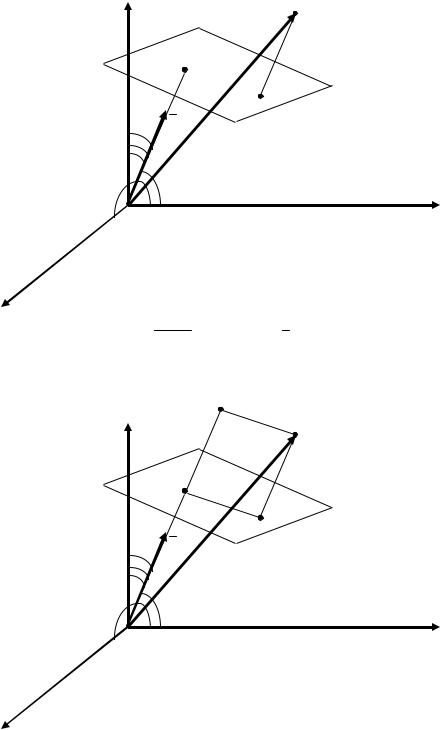
Расстояние от точки до плоскости

Пусть дана точка M 0 x0;y0;z0 и плоскость , заданная нормальным уравнением: x cos y cos z cos p 0. Найдем расстояние от точки M 0 до плоскости . Обозначим искомое расстояние через M 0, . Сделаем рисунок.

Из нормального уравнения плоскости известны расстояние от начала координат до плоскости (OP ), равное p и координаты единичного нормального вектора

e cos ;cos ;cos (ссылка).

25

P

x

Расстояние от точки до плоскости – это расстояние от точки до ее проекции на

x

Определим вектор OM 0

26

x

и найдем проекцию вектора OM 0 на вектор e , которую обозначим OK .

x

27

M 0,l x0 cos y0 sin p .

Сравнив полученное выражение с левой частью нормального уравнения плоскости, получим правило.

ПРАВИЛО 1. Для того чтобы найти расстояние от точки до плоскости, необходимо координаты точки подставить в левую части нормального уравнения плоскости и взять полученное число по модулю.

ПРАВИЛО 2. Если при подстановке координат данной точки в левую часть нормального уравнения плоскости получается положительное число, то данная точка и начало лежат по разные стороны от плоскости, если получается число отрицательное, то данная точка и начало координат лежат по одну сторону от плоскости.

ПРАВИЛО 3. Если при подстановке координат двух заданных точек в левую часть нормального уравнения плоскости, получаются числа одного знака, то точки лежат по одну сторону от плоскости, если получаются числа разных знаков, то точки лежат по разные стороны от плоскости.

Пример. Найти расстояние от точки A(4; 1;3) до плоскости :

3x y 2z 5 0.

Решение. Для решения задачи воспользуемся правилом 1. Приведем общее уравнение плоскости к нормальному виду.

В левую часть полученного нормального уравнения подставим координаты точки A и возьмем полученное число по модулю.

Пример. Найти расстояние между плоскостями : 2x y z 4 0 и :

4x 2y 2z 7 0.

Решение. Понятие расстояния между плоскостями имеет смысл, если плоскости параллельны. Проверим, параллельны ли плоскости и . Плоскости заданы общими уравнениями. Общее уравнение плоскости определяет нормальный вектор плоскости. Следовательно, мы можем указать

28