
472
.pdf
Рис. 3.24 |
|
Рис. 3.25 |
|
|
|
Пример. Выполнив параллельный перенос координатных осей, привести уравнение кривой y x 2 2x 2 к каноническому виду. Сделать рисунок кривой в исходной системе координат.
Решение. Выполним параллельный перенос координатных осей, положив
x X a , y Y b , где (a ,b) - координаты нового начала системы координат O1X Y . Параметры a и b определим, потребовав, чтобы после
параллельного переноса уравнение |
кривой |
стало бы |
простейшим |
(каноническим). |
|
|
|
Имеем:Y b (X a )2 2(X a ) 2=> |
Y X 2 |
2aX a 2 2X 2a 2 b |
|
=>Y X 2 (2a 2)X a 2 2a b 2. |
|
|
и свободный |
Приравняем в этом уравнении к нулю коэффициент при X |
|||
член, получим координаты точки O1: |
|
|
|
2a 2 0
=> a 1, b 1. a 2 2a b 2 0
Окончательно имеем каноническое уравнение кривой X 2 Y . Очевидно, что это парабола (рис. 3.25).
3.6 Уравнения кривых второго порядка с осями симметрии, параллельными координатным осям
Найдем уравнение эллипса с центром в точке O1 (x0;y0), оси симметрии которого
параллельны координатным осям Ох и Оу и полуоси соответственно равны a и b. Поместим в центре эллипса O1 начало новой системы координат O1x y , оси
которой O1x и O1 y параллельны соответ-
20
Рис. 3.26

ствующим осям Ох и Оу и одинаково с ними направлены (рис. 3.26 ).
В этой системе координат уравнение эллипса имеет вид |
x 2 |
|
y 2 |
1. |
||||||||||||||||
a2 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
|||
Так как x x x0, |
|
x y y0 |
|
(формулы параллельного переноса), то в старой |
||||||||||||||||
системе координат уравнение эллипса запи- |
|
|
|
|
||||||||||||||||
шется в виде |
x x |
0 |
2 |
|
y y |
0 |
2 |
1. |
|
|
|
|
||||||||
|
a |
2 |
|
|
b2 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Аналогично |
|
|
рассуждая, |
получим |
|
|
|
|
||||||||||||
уравнение гиперболы |
с |
|
центром в |
|
|
|
|
|||||||||||||
точке O1 (x0;y0)и полуосями a и b (рис. |
|
|
|
|
||||||||||||||||
3.27): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x |
|
2 |
|
y y |
|
2 |
|
|
|
Рис. 3.27 |
|
||||||||
|
0 |
|
0 |
1 |
|
|
|
|
|
|
||||||||||
|
|
a2 |
|
|
|
b2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
И, наконец, параболы, изображенные на рис. 3.28, имеют соответствующие уравнения.
Рис. 3.28
21

3.7 Формулы преобразования координат при повороте координатных осей
Повернём исходную систему координат Oxy на угол , и пусть она займёт положение O x1y1 (рис. 3.29). Обозначим через r радиус-вектор точки
M .
Очевидны соотношения:
x r cos( ) r cos cos r sin sin x1 cos y1 sin , y r sin( ) r sin cos r sin cos x1 sin y1 cos .
Окончательно:
xx1 cos y1 sin
yx1 sin y1 cos
Эти формулы являются формулами преобразования координат при повороте координатных осей на угол .
(ПАРАЛЛЛЕЬНЫЙ ПЕРЕНОС И ПОВОРОТ ОСЕЙ)
Рис. 3.29
3.8 Общее уравнение кривой второго порядка. Приведение к каноническому виду
Рассмотренные выше кривые 2-го порядка имеют канонические уравнения только относительно системы координат, специальным образом связанной с этой кривой. Относительно произвольно расположенной
22
системы координат каждой из этих кривых соответствует некоторое уравнение второго порядка вида
Ax2 2Bxy Cy 2 2Dx 2Ey F 0,
которое называется общим уравнением кривой второго порядка (A,B,C не равны 0 одновременно). Существует система координат (не обязательно декартова прямоугольная), в которой при каждом конкретном наборе коэффициентов данное уравнение может быть представлено в одном из видов, приведенных ниже. Общее уравнение кривой второго порядка может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую линию второго порядка. В зависимости от значений коэффициентов общего уравнения оно может быть преобразовано с помощью параллельного переноса начала и поворота системы координат на некоторый угол к
одному из 9 приведённых ниже канонических видов, каждому из которых соответствует определённый класс линий.
1) |
x2 |
|
|
y2 |
1 |
- уравнение эллипса; |
|||
a2 |
|
b2 |
|||||||
|
|
|
|
|
|
||||
2) |
x2 |
|
y2 |
1 - уравнение мнимого эллипса; |
|||||
a2 |
b2 |
||||||||
|
|
|
|
|
|
||||
3) |
x2 |
|
y2 |
|
1 |
- уравнение гиперболы; |
|||
a2 |
|
||||||||
|
|
|
|
b2 |
|
|
|||
4)a2x2 – c2y2 = 0 – уравнение двух пересекающихся прямых;
5)a2x2 + c2y2 = 0 – уравнение двух мнимых пересекающихся прямых (точка);
6)y2 = 2px – уравнение параболы;
7)y2 – a2 = 0 (x2 – a2 = 0) – уравнение двух параллельных прямых;
8)y2 + a2 = 0 (x2 + a2 = 0)– уравнение двух мнимых параллельных прямых;
9)y2 = 0 (x2 = 0) – пара совпадающих прямых.
Правило 1. Для приведения общего уравнения кривой второго порядка к каноническому виду первым действием необходимо путем поворота координатных осей на угол преобразовать это уравнение так, чтобы в
нем отсутствовал член с произведением координат.
Используя формулы поворота осей, имеем:
xx1 cos y1 sin
yx1 sin y1 cos
23

Выразим старые координаты через новые:
A(x1 cos y1sin )2 2B(x1 cos y1sin )(x1sin y1 cos ) C(x1sin y1 cos )22D(x1 cos y1sin ) 2E(x1sin y1 cos ) F 0.
Выберем угол так, чтобы коэффициент при произведении переменных х1·у1 обратился в нуль, т. е. чтобы выполнялось равенство
- 2Acos sin 2B(cos2 -sin2 ) 2Ccos sin 0,
т.е. (C A)sin2 2B cos2 0,
т.е. 2B cos2 (A C)sin2 .
Отсюда tg2 A2BC .
Таким образом, при повороте осей на угол α, удовлетворяющий условию tg2 A2BC , общее уравнение кривой второго порядка не содержит
слагаемое с произведением координат.
Замечание 1. Если А = С, то уравнение tg2 |
2B |
теряет смысл. В этом |
|
A C |
|||
|
|
случае cos2α = 0, тогда 2α = 90°, т. е. α = 45°. Итак, при А = С систему координат следует повернуть на 45°.
Замечание 2. Поворот на положительный угол α осуществляется против часовой стрелки и наоборот.
Замечание 3. Часто при осуществлении поворота системы координат используют иное символическое обозначение новой системы координат: Ox`y` , в силу чего и формулы, описывающие поворот осей принимают вид:
Правило 2. Для окончательного приведения общего уравнения кривой второго порядка к каноническому виду необходимо путем параллельного переноса координатных осей преобразовать это уравнение в одно
из указанных |
выше |
уравнений |
1)-9). Для |
осуществления |
этого |
в уравнении, |
описывающем |
24

кривую второго порядка используется техника выделения полных квадратов.
Параллельный перенос координатных осей (перенос начала координат в точку (x0;y0)), как действие, вторичное после поворота осей, осуществляется по следующим формулам:
X x x |
0, (или, согласно замечанию 3, |
x x x |
0, ). |
|||
|
1 |
|
||||
Y y1 y0 |
|
|
y y y0 |
|||
Пример. |
Дано |
уравнение |
кривой |
|
второго |
порядка |
5x 2 4xy 8y 2 52x |
64y 164 0. |
Выполнив |
поворот и |
параллельный |
||
перенос координатных осей, получить каноническое уравнение кривой и построить ее в исходной системе координат.
Решение. Выполняем поворот осей по формулам x x1cos y1sin ;
y x1sin y1cos .
Определим угол поворота системы координат.
tg2 |
|
2B |
4 |
, |
|
|
|
|
|
|
A C |
|
|
|
|
|
|||||
|
3 |
|
|
|
|
|
|
|
||
откуда следует, что (tg )1 2;(tg )2 |
1/2. Зная tg , |
можно найти sin и |
||||||||
cos по формулам тригонометрии: |
sin |
|
tg |
|
;cos |
1 |
|
. |
||
|
1 tg |
2 |
1 tg |
2 |
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
Если угол поворота условиться считать острым, |
то в этих формулах надо |
|||||||
брать знак плюс, и для |
tg надо взять также положительное |
решение. |
||||||
Выберем, |
например, |
угол |
поворота |
:tg 2, |
найдем |
|||
cos |
1 |
;sin |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|||
5 |
5 |
|
|
|
|
|
||
Подставим выражения для x и y |
в исходное : |
|
|
|||||
5(x12cos2 2x1y1cos sin y12sin2 ) 4(x 21cos sin (cos2 sin2 )x1y1y12sin cos ) 8(x12sin2 2x1y1sin cos y12cos2 )
52(x1cos y1sin ) 64(x1sin y1cos ) 164 0.
подставим их в (1). После вычисления коэффициентов получим уравнение:
9x12 4y12 36 |
5x1 8 |
5y1 164 0. |
В полученном уравнении выделим полные квадраты двучленов x1 x0 и y1 y 0:
9(x1 2 5)2 4(y1 5)2 36 0. |
Y |
y |
x1 |
X |
|
|
|
Выполнив параллельный перенос
25

по формулам x1 2 5 X |
,y1 |
5 Y , |
|
|
||||
получим в системе X O /Y |
уравнение кривой |
y1 |
O / |
|||||
x |
2 |
y |
2 |
1: это эллипс с полуосями |
|
x |
||
|
|
|
O |
|||||
4 |
9 |
|
|
|
|
|||
2 и 3 соответственно (рис. 3.30). |
|
|
Рис. 3.30 |
|||||
3.9 Инварианты кривых второго порядка
Исследование вида линий второго порядка может быть проведено без приведения общего уравнения к каноническому виду. Это достигается совместным рассмотрением значений так называемых основных
инвариантов линий второго порядка — выражений, составленных из коэффициентов общего уравнения кривых второго порядка, значения которых не меняются при параллельном переносе и повороте системы координат.
К инвариантам кривых второго порядка относят инварианты
относительно переноса начала координат и поворота осей:
|
A B |
|
|
A |
B |
D |
|
|
|
||||||
S A C , |
|
, |
B C |
E |
. |
||
|
B C |
|
|
D |
E |
F |
|
|
|
|
|
|
|||
Полуинвариант уравнения (инвариант относительно поворота осей):
|
|
C |
E |
|
A |
D |
|
A |
|
E |
F |
|
D |
F |
. |
В зависимости от значений величин S, , , A общее уравнение кривой второго порядка определяет одну из следующих линий:
эллипс мнимый эллипс
пара мнимых пересекающихся прямых
гипербола
пара пересекающихся прямых
26

парабола
/пара мнимых параллельных прямых
пара параллельных прямых
/
/пара совпадающих прямых
Пример. Определить тип кривой второго порядка при помощи вычисления инвариантов.
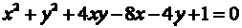 .
.
Решение. Определим тип крипой с помощью инвариантов преобразований.
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
|
|
|
1 |
2 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Очевидно, S 1 1 2, |
|
3, |
|
2 |
1 |
2 |
17, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
4 |
2 |
1 |
|
|
|
|
1 |
4 |
|
|
|
1 |
2 |
|
18 |
|
|
|
|
|
||||
|
|
|
|
|
|
, поэтому имеем гиперболу. |
||||||||||||||
|
|
|
|
|||||||||||||||||
A |
|
4 |
1 |
|
|
2 |
1 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Задачи для самостоятельного решения
Задача 1.
1.1 Написать уравнение эллипса, проходящего через точку пересечения гиперболы x 2 y 2 2 с прямой x y 2 0, если известно, что фокусы эллипса совпадают с фокусами гиперболы.
1.2. Составить уравнение гиперболы, имеющей общие фокусы с
эллипсом x 2 y 2 1 при условии, что ее эксцентриситет 1,25. 49 24
1.3. Написать уравнение такой окружности, чтобы ее диаметром оказался отрезок прямой x y 4, заключенный между осями координат.
1.4. Большая ось эллипса втрое больше его малой оси. Составить каноническое уравнение этого эллипса, если он проходит через точку
M 3, 3 .
27

1.5. Дана гипербола x 2 y 2 8. Составить уравнение эллипса, проходящего через точку M (4,6) и имеющего фокусы, которые совпадают с фокусами данной гиперболы.
1.6. Найти точки пересечения параболы y 2 8x с эллипсом, у которого правый фокус совпадает с фокусом этой параболы, большая полуось равна 4
ифокусы лежат на оси 0x .
1.7.Фокусы гиперболы лежат в точках F1( 7,0) и F2( 7,0).
Гипербола проходит через точку A 2,0 . Найти уравнения ее асимптот.
1.8. Найти параметр |
p параболы y 2 2px , если известно, что эта |
|
парабола проходит через точки пересечения прямой y x |
с окружностью |
|
x 2 y 2 6x 0. |
|
|
1.9. Найти точки пересечения параболы y 2 4x с прямой, проходящей |
||
через фокус этой параболы параллельно ее директрисе. |
|
|
1.10. Через правый |
фокус гиперболы 4x 2 5y 2 |
20 проведены |
прямые, параллельные ее асимптотам. Определить точки пересечения этих прямых с гиперболой.
1.11. Написать уравнение окружности, проходящей через начало координат, центр которой совпадает с фокусом параболы y 2 8x .
1.12. Оси гиперболы совпадают с осями координат. Гипербола проходит через точки пересечения параболы x 2 2y с прямой x 2y 6 0. Составить уравнение этой гиперболы.
1.13.Эллипс проходит через точку пересечения прямой 3x 2y 7 0
спараболой y 2 4x (взять точку с меньшей абсциссой). Оси эллипса
совпадают с осями координат. Составить уравнение этого эллипса, если его эксцентриситет равен 0,6.
1.14. Эксцентриситет гиперболы в 2 раза больше углового коэффициента ее асимптоты. Гипербола проходит через точку M (3, 1), и ее
действительная ось лежит на оси 0x , а центр - в начале координат. Найти точки пересечения этой гиперболы с окружностью x 2 y 2 10.
1.15. Написать уравнение параболы, вершина которой находится в начале координат, а осью симметрии является ось 0x , если известно, что
расстояние от ее фокуса до центра окружности x 2 y 2 10x 8y 25 0
равно 5.
1.16. Составить каноническое уравнение эллипса, правая вершина
которого |
совпадает с |
правым фокусом гиперболы 8x 2 y 2 |
8. Эллипс |
||||
проходит |
через точки |
пересечения параболы y 2 12x |
с |
гиперболой |
|||
8x 2 y 2 8. |
|
|
|
|
|
||
1.17. Вычислить расстояние от фокуса гиперболы |
x 2 |
|
y 2 |
1 до ее |
|||
5 |
4 |
||||||
|
|
|
|
|
|||
асимптоты. Найти эксцентриситет этой гиперболы.
28

1.18. Найти точки пересечения параболы y 2 x с окружностью,
которая проходит через начало координат, имеет центр на оси 0x и радиус, равный 5.
1.19.Составить уравнение эллипса, если его фокусы совпадают с
фокусами гиперболы x 2 y 2 1, а эксцентриситет эллипса равен 3/5. 5 4
|
|
1.20. Окружность имеет центр в левой вершине гиперболы |
x 2 |
|
y 2 |
1 |
|||||||||||
|
|
16 |
4 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и радиус, |
равный вещественной |
полуоси |
этой гиперболы. Найти |
точки |
|||||||||||||
пересечения этой окружности с асимптотами гиперболы |
x 2 |
|
y 2 |
1. |
|
|
|
||||||||||
16 |
4 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1.21. |
Написать |
уравнение |
гиперболы, |
имеющей |
|
эксцентриситет |
|||||||||
3/2, |
если известно, что |
ее фокусы совпадают с |
фокусами |
эллипса |
|||||||||||||
x 2 |
|
y 2 |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1.22. Составить уравнение окружности, диаметром которой служит |
|||||||||||||||
отрезок прямой x y 4, вырезанной параболой y 2 2x . |
1x 2 |
|
|
|
|
|
|||||||||||
|
|
1.23. |
Найти расстояние от |
фокуса |
параболы y |
|
до |
прямой |
|||||||||
3x 4y 2 0. |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1.24. |
Написать |
уравнение |
окружности, |
проходящей |
через |
точки |
|||||||||
M (3,0) |
и |
N ( 1,2), |
если |
известно, что |
ее |
центр |
лежит |
|
на |
прямой |
|||||||
x y 2 0.
1.25. Вычислить расстояние от центра окружности x 2 y 2 10x до
асимптот гиперболы |
x 2 |
|
y 2 |
1. |
|
|
|
20 |
5 |
|
|
||||
|
|
|
|
|
|
||
1.26. Составить каноническое уравнение эллипса, сумма полуосей |
|||||||
которого равна 8, а расстояние между фокусами равно 8. |
|||||||
1.27. В эллипс |
|
x 2 |
|
y 2 |
1 вписан прямоугольник, две |
||
|
49 |
24 |
|||||
|
|
|
|
|
|
||
противоположные стороны которого проходят через фокусы. Вычислить площадь этого прямоугольника.
1.28. Составить уравнение окружности, проходящей через точки A (5,0) и B 1,4 , если центр ее лежит на прямой x y 3.
1.29.Написать каноническое уравнение эллипса, у которого эксцентриситет равен 0,8, а большая полуось больше малой полуоси на две единицы.
1.30.Найти каноническое уравнение гиперболы, проходящей через
точку M |
40,2 и имеющей асимптоты y |
1x . |
|
|
3 |
29
