Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

472

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2110 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

4a (x c)2 y 2 4a2 4xc

a2 (x c)2 a2 y 2 a4 2a2 xc x2c2

a2 x2 2a2 xc a2c2 a2 y 2 a4 2a2 xc x2c2 a2 x2 a2c2 a2 y 2 a4 x2c2 0

x2 (c2 a2 ) a2 (c2 a2 ) a2 y2 0 x2 (c2 a2 ) a2 y 2 a2 (c2 a2 ).

Введем обозначение с2 – а2 = b2 (геометрически эта величина - меньшая полуось), тогда:

a2b2 b2 x2 a2 y 2 ,

откуда следует, что
	x2	y2	1
	a2	b2

Полученное уравнение - каноническое уравнение гиперболы.

Исследование формы гиперболы по ее уравнению

Установим форму гиперболы, пользуясь ее каконическим уравнением.

1. Уравнение	x2	y2	1	содержит переменные x и у только в четных
	a2	b2

степенях. Следовательно, гипербола симметрична относительно осей Ox и Oy, а также относительно точки O(0;0), которую называют центром

гиперболы.

2. Найдем точки пересечения гиперболы с осями координат. Положив y=0 в каноническом уравнении, находим две точки пересечения гиперболы с осью Ox: (a;0) и (-a;0). Положив x=0 , получаем y2=-b, чего быть не может. Следовательно, гипербола ось Оу не пересекает.

Точки (a;0) и (-a;0)	называются вершинами гиперболы, а отрезок [-
a;a] действительной	осью, число a — действительной полуосью
гиперболы.

Отрезок, соединяющий точки (0;b) и (0;-b) называется мнимой осью, число b - мнимой полуосью. Прямоугольник со сторонами 2a и 2b называется

основным прямоугольником гиперболы.

3. Из канонического уравнения следует, что уменьшаемое	x2	1, или, что то
	a2

же самое, x a . Это означает, что точки гиперболы расположены справа от

прямой x=a (правая ветвь гиперболы) и слева от прямой x=-a (левая ветвь гиперболы).

4. Из канонического уравнения гиперболы видно, что когда

возрастает, то

возрастает. Это следует из того, что разность

сохраняет

постоянное значение, равное единице.

Из сказанного следует, что гипербола имеет форму, изображенную на рис. 3.11 (кривая, состоящая из двух неограниченных ветвей).

Асимптоты гиперболы

Определение. Прямая L называется асимптотой неограниченной кривой K, если расстояние d от точки M кривой K до этой прямой стремится к нулю при неограниченном удалении точки M вдоль кривой K от начала координат.

Покажем, что гипербола

имеет две асимптоты:

и y

x .

Так как прямые

x ,

гипербола

симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти.

Возьмем			на	прямой	Рис. 3.12

y	b	x точку	N,	имеющую ту


	a

же абсциссу х, что и точка M(x;y) на гиперболе y ba x2 a2 (рис. 3.12), и

найдем разность ΜΝ между ординатами прямой и ветви гиперболы:

(x x2

a2 )

x2 a2 )(x

x2 a2 )

x2 a2

Как видно, по мере возрастания х знаменатель дроби увеличивается; числитель — есть постоянная величина. Стало быть, длина отрезка ΜΝ стремится к нулю. Так как ΜΝ больше расстояния d от точки Μ до прямой, то d и подавно стремится к нулю.

Итак,			прямые		y	b	x	и

	b					a
y		x являются					асимптотами

	a
гиперболы.
	При			построении				гиперболы
целесообразно сначала построить ос-
новной			прямоугольник					гиперболы
(рис. 3.13), провести прямые,
проходящие через противоположные
вершины этого прямоугольника, —									Рис. 3.13
асимптоты				гиперболы			и	отметить

вершины гиперболы.

Уравнение равносторонней гиперболы

y=x

Определение. Гипербола (11.9) называется равносторонней (равнобочной), если ее полуоси равны (a=b).

Каноническое	уравнение		равносторонней
гиперболы	x2 y 2 a2 .				Асимптоты
равносторонней гиперболы		имеют			уравнения
y=x и y=-x и, следовательно,					являются
биссектрисами координатных углов (рис. 3.14).							y=-x

			c			Рис. 3.14
Определение.	Отношение			1	называется


			a

эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с2 – а2 = b2:

2	c2		a2 b2	b2
	a2		a2	a2
	a2		a2	a2
		b	2 1
		a	2 1
		a

Эксцентриситет характеризует форму гиперболы. Действительно, в

силу того, что

с2

2 1

1, то есть

Отсюда следует, что чем меньше эксцентриситет гиперболы, тем меньше отношение — ее полуосей, а значит, тем более вытянут ее основной прямоугольник.

Эксцентриситет равносторонней гиперболы равен 2.. Действительно,

c	a2 a2	2.
a	a

Фокальные радиусы r	(x c)2	y2	и r	(x c)2 y2	для точек правой
1			1
ветви гиперболы имеют	вид	r1 x a и		r2 x a ,	а для левой —
r1 ( x a) и r2 ( x a) .

Определение. Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/ε от него, называются директрисами гиперболы.

Уравнения директрис:

x a .

С понятием директрис гиперболы связана следующая теорема.

Теорема. Если r – расстояние от произвольной точки М гиперболы до какоголибо фокуса, d – расстояние от той же точки до соответствующей этому фокусу директрисы, то отношение r/d – величина постоянная, равная эксцентриситету.

Доказательство. Изобразим схематично гиперболу (одну из ее ветвей).

y
y
a/ε			d
			M(x, y)
			r1
	О
0		a	F1(с;0)	x

Рис. 3.15

Из очевидных

геометрических

соотношений

(рис.3.15) можно

записать:

a/ε + d = x, следовательно d = x – a/ε.

(x – c)2 + y2 = r2

x2b2

Из канонического уравнения: y

, с учетом b2 = c2 – a2:

r 2 x2 2xc c2

x2b2

2xc c

c2 x2

x a

r ac x a

Тогда т.к. с/a = ε, то r = εx – a.

Таким образом,	r	x a		.
	d	x	a

Для левой ветви гиперболы доказательство аналогично. Теорема доказана.

Кривая, определяемая

уравнением	x2	y2	1	также	есть
	a2	b2

гипербола, действительная ось 2b которой расположена на оси Оу, а мнимая ось 2a — на оси Ох. На рис. 3.16 она изображена пунктиром.

Очевидно,

что

гиперболы

Рис. 3.16

имеют

общие асимптоты. Такие гиперболы называются сопряженными.

Пример. Найти уравнение гиперболы, вершины и фокусы которой находятся
в соответствующих фокусах и вершинах эллипса	x2	y2	1.
		5
8
Решение. По условию задачи с(элл.)=a(гип.) и наоборот, а(элл.)=с(гип.)
Для эллипса имеем: c2 = a2 – b2 , таким образом,		c2 (элл.) =8-5=3. Для
гиперболы: c2 = a2 + b2, следовательно, 8=3+ b2		(рис.3.17, 3.18). Таким
образом, b2 (гип.)=5.

y	y	3
5		x
x		x
3		8
8		8
8
Рис. 3.17		Рис. 3.18
		Рис. 3.18

Уравнение гиперболы: x2 y2 1.

3 5

Пример. Составить уравнение гиперболы, если ее эксцентриситет равен 2, а

фокусы совпадают с фокусами эллипса с уравнением

Решение. Находим фокусное расстояние c2 = 25 – 9 = 16.

Для гиперболы: c2 = a2 + b2 = 16,

ε = c/a = 2;

c = 2a;

c2 = 4a2;

a2 = 4; b2 = 16 – 4 = 12. Таким

образом,

искомое

уравнение

гиперболы.

Пример. Фокусы эллипса совпадают

с фокусами

гиперболы

x 2 y 2 1.

Эллипс проходит через точку M ( 2;1,5). Составить уравнение этого эллипса.

Решение. Обозначим через a1

и b1полуоси данной гиперболы, через a

и b -

полуоси искомого эллипса. Имеем a

2 9,b 2

4, откуда c 2

a 2 b 2 13. Так

как фокусы эллипса совпадают с фокусами данной гиперболы, то и для

эллипса c 2 c12	13. Уравнение эллипса ищем в виде x 2				y 2 1. Так как
				a 2	b2
точка M ( 2;1,5)	принадлежит эллипсу, то ее
координаты удовлетворяют уравнению эллипса и, кроме того, выполнено
соотношение a 2 b2		13. Таким образом, для определения a и b имеем
систему:					y
( 2)2			(1,5)2	1;

	a 2		b2
	a 2		b2
a 2 b2 13.

				15	x
				15

Обозначив b2 t (t 0) и a 2						13 t ,
4		9		1,a 2
получим					13		t .
	13 t		4t
Решая, находим t b2 3,a 2						16 ( рис. 3.19).			Рис. 3.19
Итак, уравнение эллипса					x 2		y 2	1.

					16		3

Пример. Найти уравнение траектории точки, которая, перемещаясь по плоскости xOy, остаётся в два раза дальше от точки A (4,0), чем от прямой

x 1. (рис. 3.20)

(x 1)i. Должно

Решение. Рассмотрим векторы A M (x 4)i y j и

B M

быть

, т.е.

(x 4)2 y 2 2

x 1

. Возводя в квадрат, получим

A M

B M

(x 4)2 y

2 4(x 1)2 . После упрощения имеем гиперболу

x 2

y 2

4 2

(рис. 3.20).

Рис. 3.20

3.4 Парабола и еесвойства

Определение. Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

		(ПАРАБОЛА)
Расположим начало координат посередине между фокусом и
директрисой (рис.3.21). y		M(x;y)
A

0	F	x
p/2	p/2

Рис. 3.21

Величина р (расстояние от фокуса до директрисы) называется

параметром параболы.

Выведем каноническое уравнение параболы. Из геометрических соотношений:

AM = MF; AM = x + p/2;

MF2 = y2 + (x – p/2)2 (x + p/2)2 = y2 + (x – p/2)2

x2 +xp + p2/4 = y2 + x2 – xp + p2/4

y2 = 2px.

Полученное уравнение называется каноническим уравнением параболы.

Уравнение директрисы:

x = -p/2.

Исследование форм параболы по ее уравнению

1.В каноническом уравнении параболы переменная у входит в четной степени, значит, парабола симметрична относительно оси Ох; ось Ох является осью симметрии параболы.

2.Так как ρ > 0, то из канонического уравнения параболы следует, что x 0 . Следовательно, парабола расположена справа от оси Оу.

3.При x 0 имеем у = 0. Следовательно, парабола проходит через начало координат.

4.При неограниченном возрастании x модуль у также неограниченно

возрастает. Парабола y2 = 2px имеет вид (форму), изображенный на рис. 3.21. Точка О(0; 0) называется вершиной параболы, отрезок FM = r называется фокальным радиусом точки М.

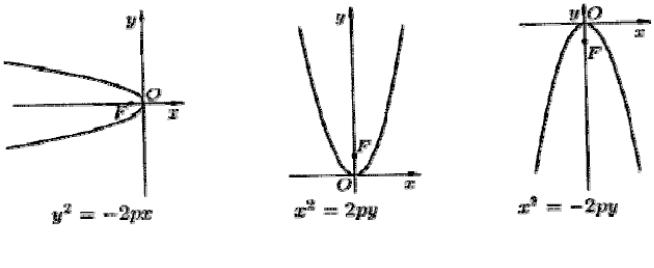
Уравнения y2 = -2px, x2 = 2py, x2 = -2py (p>0) также определяют параболы, они изображены на рис. 3.22.

Нетрудно показать, что график квадратного трехчлена

, где A≠0, B и С любые действительные числа, представляет собой параболу в смысле приведенного выше ее определения.

Рис. 3.22

Пример. На параболе у2 = 8х найти точку, расстояние которой от директрисы равно 4.

Решение. Из уравнения параболы получаем, что р = 4.

r = x + p/2 = 4,

следовательно x = 2; y2 = 16; y = 4. Искомые точки: M1(2; 4), M2(2; -4).

Пример. Найти уравнение траектории точки, которая, перемещаясь по плоскости xOy, равноудалена от точки A (2,1) и от оси ординат.

Решение.			Рассмотрим		векторы
	(x	2)i (y 1)j				и
A M	(x	2)i (y 1)j				и
	x i.
B M	x i.
По условию задачи				A M	B M	,

значит

(x 2)2 (y 1)2 x => (x 2)2 (y 1)2 x 2 => y 2 2y 1 4x 4 =>

y 2 2y 1 4x 4 =>
(y 1)2 4(x 1).
Обозначим x 1 X , y 1 Y ,
тогда относительно системы
координат X O1Y имеем параболу
.Y 2 4X (рис. 3.23 )	Рис. 3.23
	Рис. 3.23

3.5 Формулы преобразования координат при параллельном переносе координатных осей

Пусть оси O1X и O1Y координатной системы O1X Y параллельны осям

O x и O y	исходной системы координат Oxy. Допустим, что точка M в
исходной	системе координат	имеет координаты x и y , т.е.	M (x ,y );
относительно же системы O1X Y		та же точка имеет координаты X	и Y , т.е.

M (x ,y ) и M (X ,Y ). Установим связь между старыми координатами (x ,y )

точки M и её новыми координатами (X ,Y ). Согласно рис. 3.24 получим, что

r O O1 R. Если O1(a ,b) - относительно системы Oxy, то y Y b ; x X a .

Эти формулы являются формулами преобразования координат при параллельном переносе координатных осей.

(ПАРАЛЛЛЕЬНЫЙ ПЕРЕНОС И ПОВОРОТ ОСЕЙ)

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 2110 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.8 Mб8453.pdf
#
15.11.20221.83 Mб0457.pdf
#
15.11.2022277.89 Кб046.pdf
#
15.11.20221.86 Mб1462.pdf
#
15.11.2022278.22 Кб047.pdf
#
15.11.20221.92 Mб0472.pdf
#
15.11.20221.94 Mб1476.pdf
#
15.11.20221.94 Mб2477.pdf
#
15.11.20221.94 Mб4479.pdf
#
15.11.2022278.23 Кб048.pdf
#
15.11.20221.94 Mб3481.pdf