Автоматический газовый хроматографический анализ

yi yi M yi ,

где М[yi] — математическое ожидание базисного сигнала

M yi M y0 M υ i t ,

M[y0], M[υ] — математическое ожидание базисного сигнала в начале участка и скорости линейного дрейфа), получим для ошибки фильтра в стационарном режиме (пренебрегая начальным переходным процессом):

оценке yб.с фильтром. Оценим σ2б.с (т.к. ошибки независимы, оценку их значений можно провести по отдельности):

i i

σб2.с lim γ2 1 γ q 1 γ j B j q ,

i j 0 q 0

где B(j — q)— корреляционная функция случайных ошибок измерения. Считая соседние отсчеты yi некоррелированными, получим для σ2б. с:

т.к. в большинстве случаев γ << 1.

Определим динамическую погрешность ф.дин в установившемся режиме. Для этого найдем предельное значение при t —> ∞ члена, стоящего в круглых скобках выражения (117). Выразив М[yi] через М[y0] и М[υ], получим:

где

ζ γ i 1 γ j 1 1 γ i 1;

j 0

γ i j 1 γ j .

j 0

141

Оценим точность измерения дрейфа базисного сигнала на выходе фильтра. Будем считать дрейф равным первой разности значений базисного сигнала:

(при наличии помех вместо σш в выражения оценок погрешностей фильтра подставляются σп).

При линейном дрейфе систематическая погрешность в измерении скорости дрейфа υ на выходе фильтра будет отсутствовать, однако при скачках (разрывах) скорости или нелинейном дрейфе появится систематическая составляющая, оцениваемая аналогично (119) или (120),

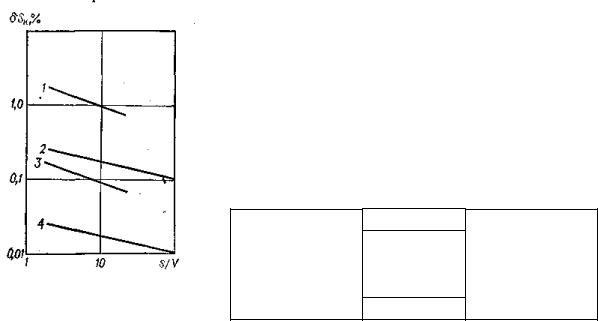
рис. 56.

Рис. 56. Зависимость δSK = f(s/υ) при различных значениях параметра µυ/A и ошибки измерения скорости дрейфа Δυ/υ (s — порог чувствительности селектора по производной):

В случае обнаружения

142

пика алгоритмами, работа которых не зависит от текущего значения базисного сигнала, динамическая погрешность измерения базисного сигнала на выходе фильтра может быть скомпенсирована, если в уравнение фильтра ввести слагаемое, пропорциональное дрейфу базисного сигнала. При этом измерение дрейфа можно провести на выходе аналогичного фильтра, но с большим сглаживанием, т.е. с β << γ. Это вполне реально осуществить, т.к. υ меняется медленнее и ее относительное значение меньше, чем скорость изменения сигнала у', поэтому степень сглаживания υ может быть сделана значительно большей, чем у', без внесения существенных искажений. Тогда выражение (95) примет вид:

где φ — весовой коэффициент. Примем φ равным коэффициенту при М[υ]Δt в (120). Тогда выражение для динамической погрешности фильтра будет иметь вид:

начале хроматограммы, там, где пики отсутствуют. При скачках базисной линии погрешность достаточно быстро возвращается к малым значениям. Аналогично определяется σ2б. с:

Сравнивая (123), (124) с (118) и (120), можно заметить, что введение компенсации систематической части погрешности фильтра ф увеличивает

значения σ2б. с при некоторых значениях γ и β. Интересно отметить, что при γ = β фильтр перестает работать.

Для уменьшения затрат времени на вычисления, что особенно важно при реализации алгоритма обработки в СВУ, величины γ, β целесообразно

143

принимать равными 2–n, что позволяет заменить операцию умножения операцией сдвига.

Приведем значения (σ2б.с /σш)2 при некоторых γ и β:

При оценивании параметров базисного сигнала по скользящей выборке методами максимального правдоподобия инерционность достигается расширением выборки по сравнению с выборками, по которым принимается решение о пике.

В предположении линейного дрейфа (аппроксимация базисного сигнала полиномом первой степени) система уравнений для получения оценок максимального правдоподобия (см. подразд. 6.3) примет вид:

Nб yi k M y0 M υ k t 0;

k 1

Nб yi k M y0 M υ k t k t 0,

k 1

где Nб — объем выборки для оценки базисного сигнала.

144

Дисперсия σ2б.с (в предположении белого шума):

6.3. Автоматическое обнаружение пиков и их характерных точек в хроматографическом сигнале

6.3.1. Обнаружение пика по текущим значениям хроматографического сигнала.

Задача обнаружения пика в сигнале, поступающем в обработку, может быть сведена к проверке гипотезы Н1 о принадлежности некоторой выборки Y текущих значений сигнала пику против альтернативной гипотезы Н0 образования выборки Y шумом. Правило выбора решения строится так, чтобы мимизировать некоторый функционал — средний риск (байесовские решения). Это выполняется при

где L(Yi) — отношение правдоподобия в i-й точке; W(Yi|Hi) и W(Yi|H0)— функции правдоподобия — условные плотности вероятности выборки Y; при наличии (Hi) и отсутствии (H0) сигнала; Ш — порог, превышение L(Yi) которого соответствует принятию гипотезы Hi о наличии пика в сигнале.

Величина порога Ш выбирается из условия обеспечения заданной вероятности а ложного обнаружения (критерий Неймана — Пирсона):

lnШ

где F(ln Ш) — значение интегральной функции распределения отношения правдоподобия при гипотезе Н0 и значении аргумента ln Ш.

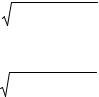
Функция правдоподобия выборки из N зависимых случайных величин при условии справедливости гипотез H0 и Hi имеет вид:

145

,

где (Yi—M[Y])—вектор-столбец центрированных значений сигнала; (Y — M[Y])T — транспонированный вектор (вектор-строка); В — ковариационная матрица размера N×N с элементами В = σkσqRkq и детерминантом det Bkm.

Тогда логарифм отношения правдоподобия будет равен:

Обозначая M[Yi]TB-1km = Ui, можно ln L(Yi) представить в виде разности скалярных произведений:

Математическое ожидание сигнала включает в общем случае значение базисного сигнала:

M yk Fk M yб.с .

Для простоты выкладок здесь и далее предполагается, что операции обнаружения предшествовала операция коррекции базисного сигнала либо значения его известны. Тогда, заменяя M[yk] на значения Fk модели ожидаемого сигнала, получаем критерий (128) в виде

146

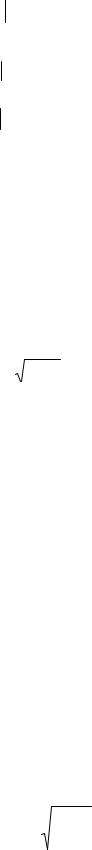
математическим ожиданием и дисперсией:

M l H1 M Yi Т Bkm1 Fk Fk ТBkm1 Fk N uk Fk 2

k 1

M l H0 0

D l H0 M l M l 2 M Fk ТBkm1 Yk Yk ТBkm1 Fk Fk ТBkm1 M Yk Yk Т Bkm1 Fk

Можно показать, что D[l|H1] = D[l|H0] = D[l] и для вероятности ложного обнаружения получим (см. (127)):

Откуда оценка порога Гг будет:

где ха — процентная точка нормального распределения. Вероятность правильного обнаружения:

Pп.о 0,5 xa .

В случае некоррелированности отсчетов в выборке алгоритм для процедуры обнаружения упрощается. Тогда B-1km = 0 (k ≠ q) и B-1km =σш (k = q). Критерий обнаружения (129) будет

Значение порога Гг определится из (130) (при наличии помех вместо σш подставляется σп):

Учитывая, что при изменении а в реальных пределах от 0,001 до 0,02

147

величина ха меняется от 3,09 до 2,05, получим:

Величина σl может быть вычислена либо непосредственно из измерений l(Yi) на начальном участке хроматограммы, либо по значению σш, определенному также в начале анализа на участках без пиков, или по величинам невязок при аппроксимации пика его моделью.

Таким образом, процедура обнаружения состоит в вычислении суммы взвешенных значений сигнала (133) на i-й выборке и сравнении полученной суммы с порогом Гг (132). Если неравенство (133) не выполняется, то выборка сдвигается на шаг t и процедура повторяется. Абсцисса начальной точки tн = q t q-й выборки, на которой произошло обнаружение (выполнение критерия (133)), принимается за начало пика. Алгоритм (128) или (133) является асимптотически оптимальным и представляет в пределе реализацию согласованного фильтра. При отсутствии шумов выход согласованного фильтра l нарастает на участке 0 ≤ t ≤ Tc, достигает при t = Тс максимума l(Yi)= Ес (Ес — энергия, численно равная энергии сигнала) и затем спадает до 0.

В простейшем случае при наличии только шума с постоянной спектральной плотностью G(ω), некоррелированного на интервале t, вероятность обнаружения пика на q-й выборке Рп. оq будет:

Здесь ωQ(l)—плотность вероятности значений решающих функций (128) или (133), соответствующая многомерному нормальному закону распределения

Корреляционные моменты в ковариационной матрице Вkl на интервале, равном длине выборки, не равны 0 даже при некоррелированности между собой отсчетов в выбойке:

Rkl M N N M ya M yb ya yb , a 1 b 1

где yа , yb — центрированные значения сигнала в точках а и b выборок k и l.

Поскольку при а ≠ b отсчеты некоррелированны, то

148

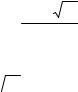
Rkl N M ya M ya q M ya 2 ш N M ya M ya q .

Тогда для оценки момента обнаружения получим (М[tн] отсчитано от первого отсчета первой выборки)

q 1

Отклонение модели от реального сигнала приводит к снижению энергии функции l, а значит, ухудшению условий обнаружения. Однако на практике иногда идут на это с целью упрощения реализации алгоритма обнаружения. Например, используют более простые описания сигнала (треугольником, параболой и т. п.). Крайним проявлением такого рода упрощений является использование модели прямоугольной формы. Тогда алгоритм (133) будет состоять в сравнении выборочных средних (или просто суммы (интеграла) выборочных значений сигнала) с порогом:

k 1

(по-прежнему yi+k представляют собой скорректированные на базисный значения обрабатываемого сигнала).

Порог Гс на основании критерия Неймана — Пирсона выбирается, исходя из заданной вероятности Рл.о.

Pл.о 0,5 Φ ГсNσшN a ,

откуда

Гс xa σш N .

Аналитическое исследование влияния параметров алгоритмов на качество получаемых оценок (136) затруднено из-за большого объема вычислений, трудности учета в (128) и (133) ошибки от квантования по времени и, как следствие, случайного характера смещения пика относительно узлов квантования.

При различных реализациях. Поэтому эти исследования были проведены методом математического моделирования, их результаты приведены далее.

Значительное упрощение реализации алгоритма (133) достигается при использовании выборки из одного отсчета. Критерий обнаружения в этом случае примет вид

При обнаружении теряются начальная и конечная части пика, которые

149

при отсутствии шума и гауссовой модели пика можно оценить:

где δSон — отношение потерянной за счет запаздывания в обнаружении пика площади к общей площади пика;

следует, что величина δSон практически независима от ширины пика μ и его асимметрии, а определяется отношением yτ/A (рис. 57). При μ → ∞ реализуется аналоговое обнаружение.

Рис. 57. Составляющие погрешности оценки площади δSобн от запаздывания в обнаружении по алгоритму (128) начала (δSон) и конца (δSок) пика при различных значениях μ* (по оси абсцисс в скобках указаны примерные пределы интегрирования Т гауссова пика (в ед. μ), соответствующие данным величинам уτ/A)

Вероятность правильного обнаружения будет зависеть от значения ожидаемого сигнала:

Если отношение сигнал/шум в зоне обнаружения М[yi]/σш будет равно хα,, то Рп.о = 0,5 (рис. 58). Из рис. 58 следует, что при изменении (увеличении) допустимой величины вероятности ложных обнаружений α на порядок кривые Рп.о смещаются несколько влево, но значения Рп.о такие, что Рпр = 1 — Рпо = α, достигаются при М[yi]/σш = 3 … 6.

150