
Автоматический газовый хроматографический анализ
..pdf
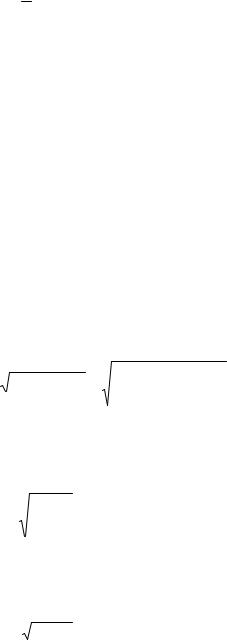
Рис. 39. Зависимость А*/А = f(u) при различных значениях φ:
1 – 0,344; 2 – 0,531; 3 – 0,688; 4 – 0,938; 5 – 1,375
Оценим влияние фильтра на шум. Если на вход линейного аналогового фильтра с передаточной функцией Н(jω) подать стационарный шум с энергетическим спектром G(ω), то энергетический спектр и корреляционная функция шума на выходе фильтра будут:
G ω * H ω 2 G ω ,
B τ * H ω 2 G ω cosωτdτ .
0
В случае подачи на вход этого фильтра шума первого порядка, образовавшегося вследствие прохождения белого шума через инерционное звено с постоянной времени Т (детектор, усилитель и т. п.), шум на выходе фильтра будет иметь G(ω)* и В(ω)*, определяемые выражениями:
G ω * |
σш |
|
|
1 |
|
|
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 ω2T 2 1 ω2T 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
ω |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ф |
|
|
τ |
|
|
|
τ |
|
|
|||||
|
|
σш |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
* |
|
|
|
|
|
σ ш |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
B ω |
|
ω |
0 |
|
|
4ω |
0 |
T 2 |
T 2 |
T exp |
T |
Tф exp |
T |
|
, |
|||||||||||
|
|
|
|
|
|
|
|
|
ф |
|
|
|
|
|
|
|
|
|
|
|
ф |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где ω0 — граничная частота шума; Tф — постоянная времени фильтра.
Среднеквадратичное отклонение выходного шума:
* |
|
|
1 |
|
. |
σш σш |
|
|
|
|
|
4ω |
0 |
T T |
|
||
|
|
ф |
|
|
Характеристики шума, прошедшего цифровой фильтр, можно получить аналогично, представив входной шум как решетчатый стационарный случайный процесс с корреляционной функцией:
121
B l t 1 q n k t n k l t . q k 1
Тогда
G ω t * B l t exp jωm T ,
m
m m
B l t * h q t h r t B l q r t ,
q m r m
где h(q t)—импульсная характеристика фильтра. Для фильтра по (93) имеем:
|
2m |
m |
|
|
|
B l t * B l q |
t Fk Fk q . |
|
|
||
|
q 2m |
k m |
|
|
|
Для среднеквадратичного значения шума получим: |
|
||||
|
B 0 B |
2m |
m |
|
|
σ*ш |
B q t Fk |
2 . |
(100) |
||
|
|
q 2m |
k m |
|
|
При действии на входе фильтра белого шума выражение (100) упростится
|
m |
|
|
σ*ш σш |
Fk2 . |
(101) |
|
|
k m |
|
|
Например, в случае фильтра скользящего среднего |
|
||
σ*ш σш |
1 |
. |
(102) |
|
|||
|
2m 1 |
|
|
Таким образом, ослабление шума пропорционально корню квадратному из числа точек в «окне» фильтра ωф, при этом даже в случае белого шума на входе фильтра шум на его выходе будет скоррелирован.
На рис. 40 приведены кривые подавления шума полиномиальными фильтрами с n = 1, n = 2 и n = 4. Наиболее эффективно подавляет шум фильтр скользящего среднего: подавление в этом случае при т = 2 такое же, как и фильтром п = 2 и т = 5 или п = 4 и т = 8. При больших т изменение п и типа фильтра на его эффективность влияет меньше. Полоса пропускания фильтра с увеличением т уменьшается, например при п = 2 это уменьшение составляет примерно 50 Гц: с 20 Гц при т = 8 до 70 Гц при т = 2. Качество сглаживания при повторной фильтрации зависит от числа повторов и в несколько меньшей степени (рис. 41).
122
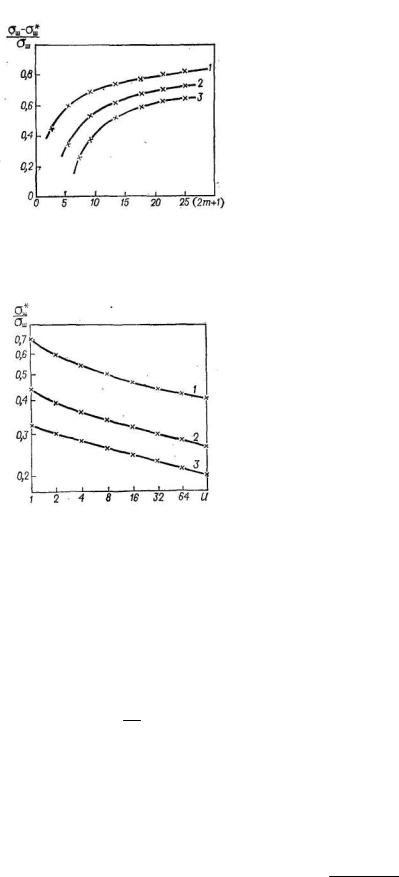
Рис. 40. Эффект ослабления нормального шума полиномиальными фильтрами: значения п: 1 – 2; 2 – 2; 3 – 4
Рис. 41. Снижение шумов при многократной фильтрации данных фильтрами с n = 2: значения т: 1 — 2; 2— 5; 3 — 12
Ввиду того, что подавление шумов значительно более эффективно, чем уменьшение амплитуды сигнала вследствие фильтрации, выходной сигнал фильтра должен иметь большее отношение сигнал/шум. Однако изучение увеличения отношения сигнал/шум показало, что кривые сигнал/шум в зависимости от параметров фильтра имеют максимум. Например, на рис. 42
представлена кривая qmax* f (μ* ), где μ* μt , для фильтра с п = 2, т = 2.
Увеличение μ* приводит к возрастанию возможного предельного отношения сигнал/шум примерно пропорциональному (μ* )0,6, однако абсолютное значение увеличения отношения сигнал/шум мало (около 4 раз при частоте опросов μ* = 14, при этом искажения амплитуды пика достигают 12%, а площади ~1 %). На рис. 43 приведена зависимость отношения сигнал/шум в
долях от максимально возможного при изменении отношения (2m 1) t :
максимум достигается при φ = 2.
123
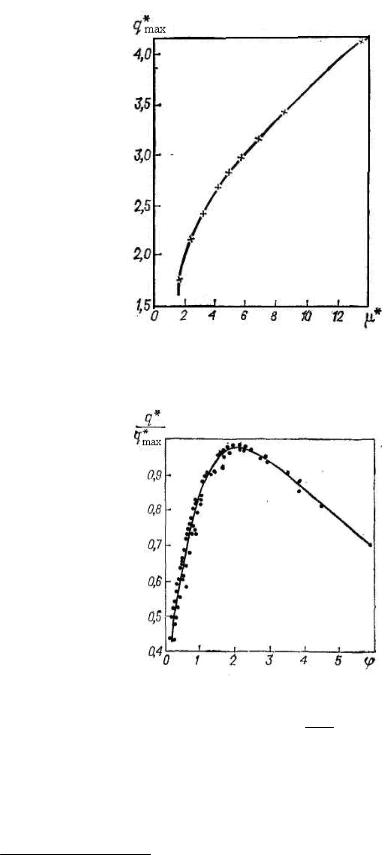
Рис. 42. Зависимость qmax* f (μ* ) для фильтра m = 2, n = 2
Рис. 43. Зависимость q** f ( )
qmax
Оценим число (2m+1) точек в выборке для оптимальной фильтрации. При п = 2 коэффициенты Fk свертки (93) будут равны:
3 3m2 3m 1 5k 2 .
Fk 2m 1 2m 1 2m 3
Учитывая только положительные значения функции F, для отношения φ получим:
124

|
|
2m 1 |
|
|
|
|
. |
2 |
3m2 3m 1 /10 |
||
Отсюда φопт = 2 обеспечивается при т между 1 и 2. При т выше 8 величина φ практически не меняется и равна 1,83. Таким образом, фильтрация с п = 2 достаточно эффективна и, согласно рис. 43, обеспечивает увеличение отношения сигнал/шум не менее 0,9 от максимально возможного. Аналогичные оценки могут быть получены и при п > 2.
Поскольку в хроматографии µ переменны, оптимизировать фильтры можно только используя адаптивную поднастройку ωф к ожидаемой µ, которая может быть найдена из регрессионного анализа (обработка ведется во вторичном времени). При обнаружении группы пиков по предварительно установленному значению т его уточненное значение находится линейной регрессией через эти точки в координатах µ — t0. Однако если среди обнаруженных попадутся очень широкие пики, это может привести к установке больших т и возможному значительному расширению будущих пиков при фильтрации. Чтобы этого не было, необходимо установить верхний предел для т, например по доверительному интервалу на разброс вокруг линии регрессии.
В заключение рассмотрим оптимизацию некоторых неполиномиальных дифференцирующих фильтров. В качестве функции F использована вторая производная гауссова сигнала. Фильтр, фактически сглаживая вторую производную сигнала, устраняет влияние базисного сигнала на обнаружение.
Ряд коэффициентов F"k определяется из уравнения второй производной гауссова пика и обрывается значением Fm+i < 0,01 F0:
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
t |
|
|
|
1 |
|
|
|
|
|
|
|||
F"k |
|
exp |
|
|
k t |
k t |
|
|
, |
(103) |
|||||
3 |
2π |
|
2 |
|
μф |
|
|
|
|
1 |
|||||
|
μф |
|
|
|
|
μф |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где μф —ширина фильтра.
Оценка µ ожидаемого пика производится при предварительном анализе хроматограммы. При работе в реальном времени µ может быть определено на основании предварительных оценок или по первым пикам хроматограммы. Для квантованных сигналов
y" *k |
m |
|
F"k yi k . |
(104) |
k m
Величина т ограничивается пределами ±m = ±4µф/Δt, за которыми F''k ≈ 0. Сумма квадратов весов, необходимая для оценки σ*y" , может быть
вычислена следующим образом:
125
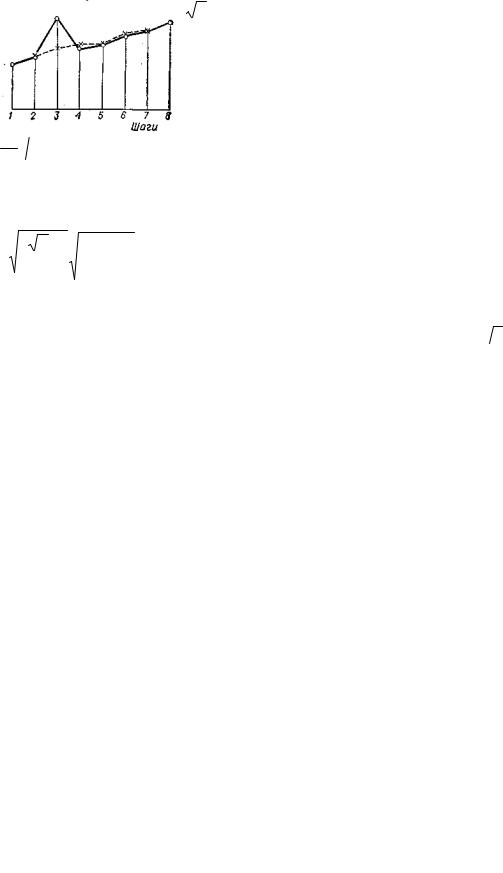
m |
|
|
3 |
t |
|
|
|
F"k 2 t |
f " τ 2dτ |
. |
|||
5 |
|
|||||
k m |
|
8μф |
π |
|||
Пусть сигнал – гауссовый пик шириной µ. Тогда, подставляя в (104) его значения yi+k и значения F''k из (103), можно видеть, что фильтрованный сигнал – действительно вторая производная пика, но с шириной
μ* 1t  μ2 μф2 .
μ2 μф2 .
Для отношения сигнал/шум на выходе получим:
q |
* |
q |
8 π |
μ |
* |
5 |
|
3 |
|
1 2 3 |
где φ определяется по (99). В этом выражении лишь последний сомножитель может быть оптимизирован. Его максимум достигается при  5 . Т.к.
5 . Т.к.
оптимум не острый, целесообразно применить меньшие значения φ: например, при φ = 1,4 снижение отношения сигнал/шум составит всего 10 %, условия разрешения пиков будут лучше.
6.1.2. Фильтрация хроматографического сигнала от импульсных помех.
Снизить ошибки от кратковременных выбросов можно, используя мажоритарные преобразования. Простейшим алгоритмом, обеспечивающим устойчивую фильтрацию при наличии выбросов, является алгоритм скользящей медианы — аналог алгоритма скользящего среднего. Под медианой med[yi t] = med[y1, y2,…, yl], где i = 1, 2, ..., l, понимается значение среднего члена y(m + 1)(l = 2m+1) или значение полусуммы средних членов ½[y(m) + y(m+1)] (l = 2m)) вариационного ряда Y, т.е. упорядоченной выборки, расположенной в порядке возрастания членов у1 ≤ у2 ≤ ... ≤уl.
Алгоритм может быть представлен в двух модификациях. Для реализации в реальном времени он имеет вид:
y*jм med yi k ; |
k 0,1, , 2m . |
(105) |
Рис. 44. Иллюстрация работы алгоритма скользящей медианы
(2m + 1 = 3)
126
Значение медианы выборки Y объема (2m+1) приписывается последнему отсчету выборки (при поступлении (2m + 1)-го отсчета первый отбрасывается).
В случае фильтрации во вторичном времени или по задержанному сигналу алгоритм (105) несколько видоизменяется
y*jм med yi k ; |
k m, m 1 , , 0, , m |
(106) |
и значение медианы приписывается среднему отсчету выборки. Пример работы алгоритма (106) при т = 1 представлен на рис. 44. При монотонном изменении сигнала медиана передает сигнал без искажения (алгоритм (106) вызывает запаздывание на шаг). При одиночном выбросе ошибка фильтрации имеет порядок приращения сигнала за шаг и не зависит от величины выброса.
При наличии протяженных выбросов (сосредоточенных помех), длящихся более чем один шаг (их можно рассматривать как групповые импульсные выбросы, далее — просто выбросы), необходимо увеличивать т: отказ фильтра не наступает, если число выбросов не превышает т. Увеличение т повышает надежность фильтра при той же вероятности α появления выбросов, но в случае фильтра, реализующего алгоритм (106), увеличивается запаздывание.
Устраняя влияние выбросов, фильтр также искажает сигнал, срезая его вершину. Максимальная ошибка при этом для гауссова пика будет
|
|
m 1 |
2 |
|
|
||
|
Ent |
|
|
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
, |
|
δAм 1 exp |
|
|
|
|
|
|
|
|
2 μ* 2 |
|
|||||
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где µ* = µ/ t.
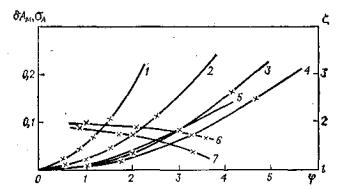
На рис. 45 показано изменение δАм в функции φ по (99) при различных значениях т. Сравнивая рис. 45, 37 и 39,
Рис. 45. Погрешности δАм вызываемые фильтрацией скользящей медианой (1—4), среднеквадратичная погрешность σА искажения амплитуды
гауссового пика (5) и величина ξ в зависимости от отношения φ:
значения т: 1 — 1; 2, 6 — 2; 3 — 3; 4, 7— 4
127

можно видеть, что искажения, вносимые алгоритмом (106) (а если не учитывать запаздывание, то и алгоритмом (105)), меньше, чем в случае фильтрации скользящим средним. Эти искажения примерно такие же, как у полиномиального фильтра с п = 2.
Кроме того, следует учесть, что ошибка δАм бывает только при попадании максимума пика в узел квантования. Усредняя δА, получим для среднеквадратичной ожидаемой погрешности искажения гауссова пика:
|
|
|
1 |
|
|
|
|
|
1 |
|
2 |
|
, |
|
σA |
|
|
|
βexp |
|
2 |
β |
|
|
|||||
12 |
|
|||||||||||||
где |
|
|
|
|
|
|
|
|
|
|
||||
|
|
m 1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
|
|
Ent |
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|||||
β |
|
|
|
|
|
. |
|
|
|
|
|
|||
|
|
μ* |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Пример изменения σА = f(φ) показан на рис. 45.
Оценим подавление шума на выходе фильтра. При фильтрации скользящей медианой нормального шума (при отсутствии полезного сигнала) среднеквадратичное значение шума на выходе:
σ*ш |
π |
σш . |
(107) |
|
4m π |
||||
|
|
|
||
Из (107) следует, что ш* |
существенно зависит от т. Для сравнения с |
|||
дисперсией шума на выходе фильтра скользящего среднего введем отношение γ:
γ |
σ*ш м |
|
π 2ь 1 |
. |
(108) |
||
σ*ш с |
4m π |
|
|||||
|
|
|
|
||||
Из (108) следует, что γ > 1 для всех m > 1, т.е. при нормальном шуме фильтр скользящей медианы уступает фильтру скользящего среднего, и тем больше, чем больше т:
(2m + 1) |
3 |
5 |
9 |
13 |
17 |
γ |
1.149 |
1.189 |
1.215 |
1.227 |
1.253 |
Увеличение отношения сигнал/шум на выходе фильтра также невелико:
ζ q* 1 σA . q σ*ш
Кривые ζ = f(φ) приведены на рис. 45: ζ < 2 и возрастает при уменьшении т. Однако при наличии выбросов с вероятностью появления α положение изменяется. В этом случае значение выходного сигнала фильтра:
128

σ*ш м |
|
σш2 αm 1kσв2 , |
|
4m |
|||
|
|
где k —некоторый коэффициент порядка (2m + l)–1; σв2 — дисперсия выбросов
(σв2 σш2 ). Для m = 1
σ*ш м 0,45σш2 0,55α2σв2
Сравнивая со значением сигнала на выходе фильтра скользящего среднего
σ*ш(с)  [(1 α)σ*ш ασв2 ] 2m1 1,
[(1 α)σ*ш ασв2 ] 2m1 1,
можно видеть, что при (σш2 ασв2 ) значение γ < 1 (см. также подразд. 6.3). Если на вход фильтра поступит острый пик, так что
y' t σш ,
то значения шума практически не будут изменять взаимного расположения членов вариационного ряда Y, т.е. независимо от т величина σ*ш(м) σш : при
малых шумах увеличивать выборку не имеет смысла.
Таким образом, использование фильтра скользящей медианы для фильтрации выбросов оказывается достаточно эффективным. Более качественную фильтрацию можно осуществить, применяя другие алгоритмы мажоритарного преобразования.
Эмпирические методы подавления импульсных помех, как и методы фильтрации, разделяются на две группы: реализуемые во вторичном и реальном времени. Все они включают две операции: обнаружение выброса и его коррекцию. Обнаружение выброса производится по его величине или длительности, которая меньше ожидаемой (например, из регрессионного анализа) ширины пика. После обнаружения границ выброса его устраняют, аппроксимируя участок выброса кривой, подобранной по точкам сигнала до и после пика.
При работе во вторичном времени для обнаружения и устранения выбросов можно ввести параболическую фильтрацию данных, аппроксимируя участок выброса параболой:
f i k a bk t ck 2 t 2 |
k m, m |
(109) |
((2m + 1) — число точек аппроксимации). Выброс определяют, контролируя невязку в центральной точке i-й параболы (k = 0):
129

i |
yi f i k |
. |
(110) |
|
|||
|
σш |
|
|
При этом на практике достаточно принять m = 2. Тогда
a 16 yi 2 4yi 1 4yi 1 yi 2 ,
b 101 2yi 2 yi 1 yi 1 2yi 2 ,
c 16 yi 2 yi 1 yi 1 yi 2 .
Поскольку |
i — случайная |
величина с |
нулевым |
математическим |
|||||||
ожиданием и σ |
≈ 1,4σш (на |
вход |
устройства |
обработки |
поступает чисто |
||||||
шумовой сигнал типа белого шума), то, если |
i ≥ γ1 = 5, можно предполагать |
||||||||||
выброс. |
Большое значение i |
наблюдается и при плохой аппроксимации |
|||||||||
параболой исходной кривой, поэтому |
i |
дополнительно |
сравнивается с |
||||||||
локальной кривизной в i-й точке: большая величина отношения |
i /ci > γ2 еще |
||||||||||
не свидетельствует о выбросе (сi |
имеет нулевое математическое ожидание), |
||||||||||
однако превышение величинами |
i и |
i/ci |
порогов γ1 и γ2 указывает на наличие |
||||||||
выброса. |
|
|
|
|
|
|
|
|
|
|
|
Величину порога γ2 можно оценить, исходя из следующих соображений: |
|||||||||||
1) предположив узкий пик в виде yi–2 = уi+2 = 0; yi–1 = yi+1 |
= p, yi = 4p |
||||||||||
(p — произвольное значение), получим |
i = 8/3р и сi = р/3, откуда условие |
||||||||||
выброса |
i/сi > γ2 = 8; |
|
|
|
|
|
|
|
|
|
|
2) для предотвращения |
принятия yi |
за выброс, если yi+1 |
является |
||||||||
выбросом (т. е. в случае, когда все yi+k |
равны 0, кроме yi+1 = |
р), |
условие |
||||||||
фиксации выброса |
i/сi > γ2 = 4; |
|
|
|
|
|
|
|
|
|
|
3)сглаженные колебательные наводки могут быть представлены как уi-2
=уi–1 = уi+2 0; yi = р; уi+1 = βp, тогда γ2 = (4 –– 6)/β и может быть использовано для устранения yi при –1 < β < 0 при всех γ2 ≥ 10.
Комбинируя эти результаты, получим условия обнаружения выброса в виде |Δi| > γ1 = 5 и i/сi > γ2 = 10. Проверка с гауссовыми пиками в шуме показала, что пики с µ более 0,4 t не выбрасываются.
Выброс можно обнаружить по его минимальной длительности τв в единицах t: τ*в = τв/ t (обычно от 1 до 4 точек), а также минимальной амплитуде Ав, задаваемых априорно.
Для выявления выброса в i-й точке фиксируется τ*в + 1 последовательных первых разностей для точек yi, уi=1, .... y τ*в+1, и определяется, есть ли среди них две большие Ав (разных знаков); кроме того, для исключения возможности фиксирования смены знака разностей на разных склонах пика определяются вторые разности, и если они имеют противоположные
130
