Суперфинишные станки для автомобильной промышленности

сравнению со шлифованием объясняются тем, что оптимальный вариант наладки находится вне исследуемого диапазона угла α = 15…45°. При наличии ограничений на максимальное значение угла α уменьшение МОиСКОсоставит примерно50 %.

Графики плотности вероятности f соответственно для трех рассчитанных вариантов наладки изображены на рис. 6.10.

Рис. 6.10. Плотность вероятности критерия K в зависимости от наладки станка: сплошная линия – α = 15°; штриховая – α = 30°;

штрихпунктирная – α = 45°

Сравнение оценок математического ожидания для критерия базирования с величиной отклонения от круглости показало, что оптимальные варианты наладки шлифовального и суперфинишного станков способствуют активному исправлению профиля поперечного сечения. Кроме того, наименьшему математическому ожиданию также соответствует наименьшее среднеквадратическое отклонение (имеют единый минимум).

201

Для оценок математического ожидания и среднеквадратического отклонения целесообразно вычислить доверительные интервалы. В случае нормально или асимптотически нормально распределенных величин при больших выборках и неизвестных параметрах распределения (определяемых по эмпирическим данным) используют, согласно работе [68], следующие формулы. Доверительный интервал для математического ожидания m, отвечающий доверительной вероятности р = 1 – q/100:

где tq – критерий Стьюдента (при р = 0,95 имеем tq = 1,960). Доверительный интервал для математического ожидания m,

отвечающий доверительной вероятности р = 1 – q/100 при нормальном распределении:

при асимптотически нормальном распределении

Результаты расчета доверительных интервалов по формулам (6.33)–(6.35) для данных из табл. 6.3 приведены в табл. 6.4.

Таблица 6 . 4

Доверительные интервалы для распределения критерия K в партии заготовок

202

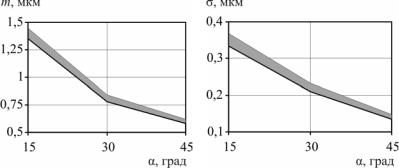
Графическая интерпретация доверительных интервалов результатов моделирования при бесцентровом суперфинишировании представлена на рис. 6.11 – для математического ожидания, на рис. 6.12 – для среднеквадратического отклонения.

Анализ табл. 6.4 показал, что с уменьшением точечных оценок математического ожидания и среднеквадратического отклонения уменьшается и величина доверительных интервалов для этих параметров.

6.3.Результаты экспериментальных исследований

ипрактической реализации наладки станков

Отклонения формы заготовок в партии носят стохастический характер. При статистическом моделировании методом Монте-Карло требуется знание законов и параметров распределений составляющих погрешностей, а также наличия корреляционных связей между ними. Подробные справочные данные по законам распределения погрешностей формы деталей при различных методах обработки в известной литературе отсутствуют. Проведены экспериментальные исследования в условиях ОАО «Саратовский подшипниковый завод». В качестве объектов бы-

203

ли взяты по две партии из 50 заготовок колец подшипников при шлифовании на неподвижных опорах и 50 валиков (поршневых пальцев) при бесцентровом шлифовании и суперфинишировании с продольной подачей.

Задача идентификации распределений решалась на основе положений теории вероятностей и математической статистики. Идентификацию эмпирической плотности распределения можно реализовать с помощью различных программных продуктов для статистического анализа данных [69]. Однако основной недостаток известных пакетов программ связан с ограниченным набором аналитических распределений (обычно 7–15 для непрерывных распределений). Поэтому разработана программа для идентификации гистограмм случайных величин. Составленная база теоретических законов распределений включает 30 известных классов непрерывных одномодальных распределений, получивших наибольшее распространение в технике: распределения Вейбулла, Стьюдента, Фишера, Парето, Пирсона, Джонсона, логистическое, логарифмически нормальное, бета-, гамма-, z-распределения и др.

Идентификация распределения проводилась в следующей последовательности:

1)по выборке данных строились гистограммы отклонения от круглости, профиля продольного сечения, амплитуд и начальных фаз гармоник поперечного сечения заготовок;

2)вычислялись оценки главных моментов распределений, коэффициенты асимметрии, эксцесса;

3)на основе анализа формы гистограмм, значений момен-

тов и графика в координатах β1 и β2 выдвигались первоначальные гипотезы о теоретической функции распределения;

4)для выбранных распределений и классов распределений рассчитывались оценки параметров распределения методами моментов и максимального правдоподобия;

5)проверялись сложные статистические гипотезы по критерию согласия на отсутствие различия между теоретическим и эмпирическим распределениями;

204

6)для распределений, удовлетворяющих критерию согласия, уточнялись параметры по методу наименьших квадратов (если первоначально они рассчитывались по методу моментов);

7)выбирался наилучший закон распределения по наименьшему значению целевойфункциивметоденаименьшихквадратов.

Гистограммы отклонения от круглости и профиля продольного сечения после бесцентрового шлифования и суперфиниширования с продольной подачей представлены на рис. 6.13.

а

б

Рис. 6.13. Отклонения от круглости (а) и профиля продольного сечения (б) после бесцентрового шлифования (а, в) и суперфиниширования с продольной подачей (б, г)

205

• начальные фазы гармоник поперечного профиля соответствуют равномерному распределению.

Для проверки склонности методов бесцентровой абразивной обработки к геометрическому наследованию отклонений формы проведены экспериментальные исследования и выполнен корреляционный анализ.

Рассчитанный коэффициент корреляции при бесцентровом суперфинишировании составил для отклонения от круглости 0,878; для отклонения продольного профиля 0,857. На основе полученных результатов о надежности корреляционных связей, а также нормальности распределения отклонения от круглости и профиля продольного сечения можно выполнить регрессионный анализ. Полученные регрессионные уравнения имеют вид:

= 0,519δ1 + 0,469.

Для статистического моделирования необходимы сведения о корреляционных связях между отдельными составляющими погрешности. Поскольку начальные фазы распределены по закону равной вероятности, корреляционный анализ требуется только для амплитуд гармоник. Коэффициент корреляции представляет собой состоятельную оценку независимо от закона распределения случайных величин.

Рассчитан коэффициент корреляции для парных сочетаний амплитуд гармоник со 2 по 9-ю, так как они имеют наибольшие абсолютные значения. Результаты приведены на рис. 6.14 для шлифования с продольной подачей, предшествующей операции суперфиниширования.

Таким образом, при статистическом моделировании необходимо учитывать корреляцию между 2-й и 5-й гармониками при шлифовании с продольной подачей и между 2-й и 3-й, 2-й и 4-й, 2-й и 8-й, 3-й и 4-й, 3-й и 5-й, 3-й и 8-й, 3-й и 9-й, 4-й и 8-й, 4-й

207

и 9-й, 7-й и 9-й гармониками при шлифовании с поперечной подачей. Анализ показал, что значимую корреляцию имеют в основном четные гармоники, например 2-я и 4-я, 2-я и 8-я, а также нечетные 3-я и 5-я, 3-я и 9-я, 7-я и 9-я. Из этого следует вывод о наличии в технологической системе периодически действующих факторов. Одним из таких факторов может быть переменная жесткость самой детали, имеющей три асимметричных отверстия. Гармоники 2, 3, 4 и 8 образуют группу взаимосвязанных коррелированных параметров, коэффициент корреляции для их сочетаний изменяется от 0,549 до 0,68. Поэтому при статистическом анализе целесообразно принять единый коэффициент корреляции в виде среднеарифметического значения 0,588.

Для проверки рекомендаций по оптимальной наладке бесцентрового суперфинишного станка модели SZZ-3 по углу перекрещивания 2λ и межосевому расстоянию 2v валков выполнены исследования на основе экстремального эксперимента. Целью являлся поиск оптимальной наладки станка, удовлетворяющей технологическим возможностям оборудования, при которой отклонения от круглости и профиля продольного сечения заготовок будут минимальны. В качестве метода исследования применен метод движения к экстремуму Бокса-Уилсона. Функция отклика задана в виде отношения исходных погрешностей геометрической формы к полученным после суперфиниширования. Указанные отклонения рассматривались отдельно.

Метод Бокса-Уилсона состоит из следующих этапов:

•постановка задачи, выбор откликов и факторов, выбор области эксперимента;

•выбор подобласти линейного приближения;

•выбор модели и плана эксперимента;

•обработка результатов эксперимента;

•интерпретация уравнения регрессии;

•принятие решений после исследования регрессии;

•определение градиента и проведение опытов вдоль этого направления;

•принятие решений после движения по градиенту.

209

Методом Бокса-Уилсона можно оптимизировать только один отклик, остальные отклики будут рассматриваться как ограничения. В процессе движения по градиенту дополнительные отклики играют роль контролирующих параметров. Движение прекращается при выходе любого из откликов за область допустимых значений илипридостиженииэкстремумаглавногоотклика.

За нулевой уровень приняты стандартные наладки станка, приведенные в руководстве по эксплуатации суперфинишного станка для обработки роликов 16: λ = 1,87° и v = 73,28 мм. При стандартных наладках достигнуты следующие значения: отклонение от круглости у = 1,1 и отклонение профиля продольного сечения уδ = 0,8.

Исходя из теоретических предпосылок, считаем, что поверхность отклика близка к линейной. Точность фиксирования параметров – средняя, поэтому выбирается средний интервал варьирования по всем параметрам – 10 %. Однако по параметру v эти значения выходят за допустимые пределы и не реализуются на станке для данного диаметра заготовки, поэтому диапазон варьирования по межосевому расстоянию уменьшен.

Стратегия метода предполагает, что в выбранной подобласти неизвестную поверхность отклика можно приблизить уравнением регрессии первой степени:

МУ(Х1, Х2) = β0 + β1Х1 + β2Х2 + β3Х1Х2,

где Х1 – межосевое расстояние валков; Х2 – угол перекрещивания осей валков.

Для уравнений первого порядка разработаны точные факторные планы. В них все факторы меняются на двух уровнях – верхнем и нижнем. Планы представляют собой перебор всех комбинаций уровней факторов. В данном случае – ПФЭ 22 обладает свойствами ортогональности и рототабельности. План эксперимента и результаты представлены в табл. 6.5, 6.6.

Для оценки значимости каждого коэффициента вычислим оценку его дисперсии:

S 2

Sbi2 = Nвоспрn .

210