
Моделирование систем
..pdf
3. ЭЛЕМЕНТЫ ТЕОРИИ ПОДОБИЯ
3.1. Понятие подобия
Особое место среди математических моделей занимают подобные. Если при аналогии двух объектов распространение свойств одного объекта на другой носит характер предположения и нуждается в проверке, то при подобии знание свойств одного объекта значит знание свойств другого объекта.
Подобие – это полная математическая аналогия при наличии пропорциональности между сходственными переменными, которая неизменно сохраняет при всех возможных значениях этих переменных, удовлетворяющих сходственным уравнениям.
Впервые понятие «подобие» появилось в геометрии. Геометрическое подобие – подобность геометрических фигур по сходственным характеристикам. Многоугольник с определенным количеством сторон n подобен другому многоугольнику с таким же количеством сторон n, если соответствующие углы многоугольников равны, а соответствующие стороны пропорциональны. Определение геометрического подобия многоугольников, на примере треугольников, состоит в следующем: треугольники подобны (рис. 3.1), если у них сходственные стороны пропорциональны, а сходственные углы равны, т.е. выполняются следующие равенства:
Рис. 3.1. Подобие треугольников
61
|
L1A |
|
L2 A |
|
|
L3 A |
m |
, |
||||
|
L |
L |
||||||||||
|
|
L |
|
|
L |
|
||||||
|
|
1B |
|
2B |
|
|
3B |
|
(3.1) |
|||
|
αA |
βA |
γA |
|
|
|||||||
|
mμ 1, |
|||||||||||
|
||||||||||||
|
αB |
βB |
γB |
|
|
|||||||
|
|
|
||||||||||
где mL и m – масштабные коэффициенты (масштабы) величин сторон и углов, характеризующие пропорциональность сходственных параметров. (Если mL и m называются масштабными коэффициентами, то величины обратные им, т.е. 1/mL и 1/m будут называться масштабами и обозначаться, соответственно, ML и M или наоборот, или вообще не делается различия между терминами «масштаб» и «масштабный коэффициент».)
На практике при геометрическом подобии используются не характеристики длин сторон многоугольника, а их координаты.
Если ввести систему прямоугольных координат x, y, то при геометрическом подобии все координаты xiA, yiA первого многоугольника пропорциональны соответствующим координатам xiB, yiB второго многоугольника, т.е. выполняются соотношения
xiA |
mx ; |
yiA |
my ; mx = my, |
(3.2) |
|
|
|||
xiB |
yiB |
|
||
где xi и yi – координаты любой точки, находящейся на отрезках прямых, определяющих контуры соответствующего многоугольника; mx и my – масштабные коэффициенты.
Данный вид подобия может существовать и в пространстве большей размерности, например трехмерном.
Дальнейшее развитие понятия подобия – аффинное подобие, при котором допускается неравенство масштабов по отдельным координатным осям. В этом случае геометрические фигуры или пространственные объекты как бы деформируются: круг превращается в эллипс, параллелепипед с неравномерными ребрами – в куб и т.п. (рис. 3.2).
62
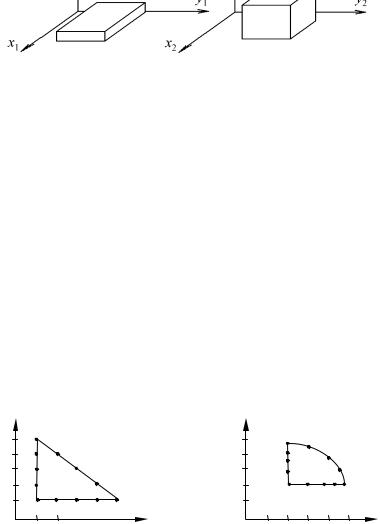
Рис. 3.2. Превращение параллелепипеда в куб
При аффинном подобии для сходственных точек в трехмерном координатном пространстве будут справедливы следующие соотношения:
xiA |
mx ; |
yiA |
my ; |
ziA |
mz ; mx my mz. (3.3) |
|
|
|
|||
xiB |
yiB |
ziB |
|||
При этом требуется введения специальных преобразующих функций, осуществляющих взаимосвязь между координатами моделей и объекта, часто – нелинейных.
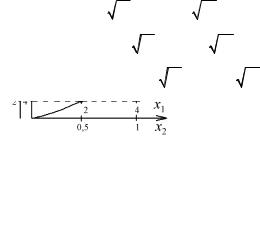
Пример 1. Установить условия аффинного подобия на рис. 3.3, отрезки линий e1 – i1 являются нелинейно сходственными линиями e2 – i2, точки e1, f1, g1, h1, i1 соответствуют точкам e2, f2, g2, h2, i2.
y1 |
e1 |
А |
|
5 |
f1 |
||
d1 |
|||
4 |
|||
|
|
||
3 |
c1 |
g1 |
|
2 |
b1 |
h1 |
|
1 |
a1 |
i1 |
y1 |
|
В |
|
5 |
e2 |
||
f2 |
|||
4 |
d2 |
||
3 |
c2 |
g2 |
|
b2 |
h2 |
||
2 |
|||
a2 |
i2 |
||
1 |
|
|
0 1 |
2 3 |
|
4 |
|
5 |
|
х1 |
0 1 |
2 3 4 5 x1 |
Рис. 3.3. Нелинейное преобразование
Уравнения для контуров e1 – i1 и e2 – i2 имеют вид x1 + y1 = 6; x22 + y22 = 24.
63
Вводятся масштабные коэффициенты Fx = x1/X1 и Fy = = y1/Y1, вид которых пока неизвестен, для уравнения первого контура можно записать:
X1Fx + Y1Fy = 6,
где X1 и Y1 – преобразованные в область B значения x1 и y1 из области A. После тождественных преобразований уравнение примет вид
|
2X |
|
|
2 |
|
2Y |
|
2 |
|
|
1 |
Fx |
|
|
1 |
Fy |
24 , |
|
y1 |
|||||||
|
õ1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
таким образом, Fx = |
|
x1 /2; Fy = |
y1 /2 и, следовательно, |
|||||
|
x2 = 2 õ1 и y2 = 2 ó1 . |
|||||||
В приведенном примере функции преобразования Fx и Fy имеют одинаковый вид, но нелинейный характер.
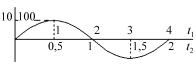
Пример 2. Даны две сходственные функции (рис. 3.4):
y1 x12 ; y2 8x22 , если масшта-
бы my = y1/y2; mx = x1/x2, соот-
Рис. 3.4. Подобные функции ветственно, равны 2 и 4, то функции подобны. В этом
примере переменные имеют различные масштабные коэффициенты по координатным осям.
Пример 3. Имеются два генератора переменного тока. Их описывает функция зависимости напряжения от времени
(рис. 3.5): |
u1 |
t |
1 |
|
и |
u2 |
t |
2 |
|
. Выраже- |
||
100sin 2 |
|
|
10sin 2 |
|
|
|||||||
|
|
|
4 |
|
|
|
|
2 |
|
|
||
ния для масштабов имеют вид mu = u1/u2, mt = t1/t2. Время, входящее в одну формулу, и время, входящее в другую формулу, имеют вполне определенный физический смысл, так как t1 и t2 имеют различные значения одной и той же величи-
64
ны t, при которых фиксируются значения различных зависимых переменных u1(t)
и u2(t).
Физическое и временное подобие имеет место
при mu = 10 и mt = 2. Масштаб mu показывает отно-
шение амплитуд напряжений u1 и u2, масштаб mt – отношение периодов T1 = 4 c и T2 = 2 c.
В общем случае временного подобия безразмерный масштаб времени представляет отношение сходственных временных интервалов, которым соответствует неизменное отношение значений или приращений подобных временных функций. Этими параметрами могут быть периоды колебаний (как в примере), постоянные времени, длительности переходных процессов, временные задержки и т.д.
Если, например, имеются две подобные САУ, то, уста-
новив время переходного процесса одной из них 1 и зная временной масштаб mt, можно найти время переходного про-
цесса другой системы: 2 = 1/mt.
3.2. Подобие физических процессов (объектов)
Любой конкретный физический процесс 0 характеризуется функциональной зависимостью f между параметрами P1, P2, ..., Pj, …, Pn. Эту функциональную зависимость Д0 = f(P1, P2, ..., Pj, …, Pn) можно графически отобразить в соответствующем n-мерном координатном пространстве x1, ..., xj, ..., xn. В этом координатном пространстве каждый параметр соотнесен с определенной координатной осью.
Аналогично в том же координатном пространстве может быть отображен другой процесс Ф0 = f(R1, ..., Rj, …, Rn), который характеризуется сходными с Д0 параметрами. Два физических процесса будут подобны, если сходственные парамет-
ры пропорциональны, т.е. если |
P1 |
m |
,..., |
Pn |
m |
n |
, а функ- |
|
|
||||||
|
1 |
|
Rn |
|
|||
|
R1 |
|
|
|
|||
65 |
|
|
|
|
|
|
|
циональные зависимости идентичны. В этом случае Д0 и Ф0 подобны.
Не все масштабные коэффициенты m1, ..., mj, ..., mn могут принимать независимые значения, вследствие того, что зависимы параметры, которые характеризуют процесс. Это делает возможным введение обобщенных характеристик подобных процессов – критериев подобия. Критерии подобия – это функции групп зависимых и независимых параметров. Если масштабные коэффициенты, в общем случае численно различны, то критерии подобия принимают одинаковые значения в сходственных точках обобщенного пространства пара-
метров x1, ..., xj, ..., xn.
Пропорциональность параметров – частный случай подобия физических процессов.
Подобие – это взаимооднозначное соответствие между объектами (процессами), при котором функции или правила перехода от параметров, характеризующих один из объектов, к параметрам, в том же смысле характеризующих другой объект, известны, а математические описания допускают их преобразования к тождественному виду.
3.3. Виды подобия
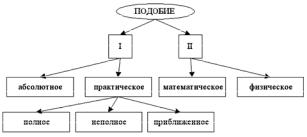
Виды подобия (рис. 3.6) различаются по двум основным признакам:
I – степень соответствия параметров оригинала и модели (абсолютное и неабсолютное или практическое подобие, которое может быть полным, неполным и приближенным);
Рис. 3.6. Виды подобия
66
II – адекватность физической природы подобных явлений (математическое подобие и физическое подобие, которое может быть механическим, тепловым, электрическим и т.п.).
Два объекта абсолютно подобны друг другу, если в сходственные моменты времени в сходственных точках пространства параметры одного объекта Pi находятся в некотором соответствии с параметрами другого объекта Ri:
Pi/Ri = mi, i = 1, 2, …, n. |
(3.4) |
Если mi = const, подобие – геометрическое, mi = var, то подобие – аффинное или физическое.
Абсолютное подобие в значительной мере носит абстрактный характер. Реализуется только в геометрических построениях и в отдельных видах математического подобия.
Практическое подобие отличается от абсолютного тем, что рассматриваются не все процессы в сравниваемых объектах. В зависимости от того, какие процессы рассматриваются, различаются полное, неполное и приближенное подобие.
Полное практическое (слово «практическое» далее опускается) подобие – подобие протекания во времени и в пространстве только тех процессов, которые существенны для данного исследования. (Если, например, электромеханические явления в синхронных генераторах полностью подобны, то все процессы изменения во времени токов, напряжений, вращающих моментов и изменение во времени и в пространстве распределения магнитных и электрических полей отличаются только масштабами. При этом тепловые явления могут быть неподобными, так как они не влияют на подобие исследуемых электромеханических процессов).
Неполное подобие – подобие протекания процессов только во времени или только в пространстве. Например, есть подобие электромеханических процессов во времени, но нет подобия распространения полей.
Приближенное подобие – характеризуется наличием допущений, приводящих к допустимым искажениям одного из процессов. Приближенное подобие бывает также полным
67
инеполным. Например, подобие генераторов, устанавливаемое по упрощенным уравнениям, которые не учитывают апериодическую составляющую тока статора и периодическую составляющую тока ротора.
По второму признаку различают математическое и физическое подобие.
Физическое подобие – когда одинакова физическая природа подобных явлений. Бывает полное, неполное и приближенное подобие. Например: механически подобным процессам ставятся в соответствие – механические, электрическим – электрические, тепловым – тепловые и т.д., т.е. модель функционирует на тех же физических законах, что и сам объект.
Математическое подобие – когда сходственные пара-
метры сравниваемых процессов различной физической природы соответствуют друг другу. Бывает полное, неполное
иприближенное.
Примеры математического подобия:
1. Уравнение переходного процесса в электрической цепи (последовательное соединение резистора R, индуктивности L и конденсатора C), включенной на переменное напряжение u, изменяющееся во времени t по синусоидальному закону с угловой скоростью :
L |
d 2q |
R |
dq |
|
q |
u sin t , |
(3.5) |
||
dt |
2 |
dt |
C |
||||||
|
|
|
|
|
|||||
где q – заряд на пластинах конденсатора С.
2. Уравнение процесса вынужденных механических колебаний в вязкой среде груза массы M на пружине жесткостью с, под действием возмущающей силы F sin t и пропорциональной скорости v движения груза силы сопротивления вязкой среды.
F = –kl, |
(3.6) |
где l – расстояние, на которое перемещается груз; k – коэффициент вязкости среды, в которой перемещается маятник.
68
M |
d 2l |
k |
dl |
cl F sin ωt . |
(3.7) |
|
dt2 |
dt |
|||||
|
|
|
|
Сходственными параметрами в данном случае будут M и L, k и R, c и C, u и F, а электрический колебательный контур может служить аналоговой моделью объекта – оригинала (колеблющегося на пружине груза), наблюдаемый процесс в колебательном контуре будет одновременно решением дифференциального уравнения, описывающего движение груза.
Таким образом, теория подобия позволяет установить наличие подобия между двумя процессами или разработать способы получения этого подобия.
Основными составляющими теории подобия являются:
1)теория размерности;
2)три теоремы подобия.
3.4.Теория размерности
3.4.1.Основные положения теории размерности
Измерить некоторую величину Р – это значит сопоставить ее с другой величиной Q той же физической природы и определить, во сколько раз Р больше или меньше Q. При этом величина Q называется единицей измерения.
Системой единиц измерения называют совокупность ус-
тановленных единиц измерения, которые подразделяются на основные и производные.
Основные физические величины – размеры единиц, кото-
рых выбираются произвольно. Единицы измерения основных физических величин также называются основными.
В системе СИ основные физические величины: длина, масса, время, сила электрического тока, температура, сила света, количество вещества (табл. 3.1). Основные единицы этой системы – метр (м), килограмм (кг), секунда (с), ампер (А), кельвин (К), моль (моль), кандела (Кд).
69
|
|
|
Таблица 3.1 |
Основные физические величины |
|
||
|
|
|
|
Наименование |
Обозначение |
Размерность |
Единица |
измерения |
|||
Длина |
l |
L |
м |
Масса |
m |
M |
кг |
Время |
t |
T |
с |
Сила тока |
i |
I |
А |
Термодинамическая |
T |
Q |
К |
температура |
|
|
|
Количество |
|
N |
моль |
вещества |
|
|
|
Сила света |
J |
J |
Кд |
Производные единицы измерения – единицы измерения остальных физических величин, которые выражаются через основные в соответствии с физическими законами, т.е. величины исходного объекта измеряются в единицах измерения величин, которые приняты в качестве основных. Например, сила, как известно, определяется по формуле
F = am. |
(3.8) |
Измеряется сила в ньютонах – производных единицах измерения, или в соответствии с (3.8) в м · кг/с2:
[F] = [L][T–2][M]. |
(3.9) |
Система единиц измерения – совокупность основных и производных единиц.
Таким образом, для установления производных единиц измерения пригодны только физические формулы в виде степенных комплексов с постоянным коэффициентом, равным единице.
Определяющее уравнение – степенной комплекс, вы-
бранный для установления производной единицы измерения.
70
