
Моделирование систем
..pdfто в условиях, когда заранее ничего, кроме области D, неизвестно, мы вынуждены выбирать х в множестве
G G q |
(4.46) |
q D
Здесь G обозначает пересечение – общую часть всех
q D
множеств G q .
Конечно, такой подход сильно ограничивает наши возможности и может привести к получению не очень хорошего проекта изделия, хотя и абсолютно надежного в том смысле, что при любых мыслимых условиях будут выполняться все заданные требования.
Для того чтобы сделать условия менее жесткими и не учитывать заведомо малореальные возможности, следует сузить множество D. Но для этого надо получить и использовать какую-нибудь дополнительную информацию о неконтролируемых факторах q. Здесь возможны различные пути. Во-первых, можно воспользоваться мнением экспертов, которые либо на основании своего опыта выдадут конкретный
набор значений q q1,..., qk , либо укажут более узкое, чем
первоначальное, множество D возможных значений q, а возможно, укажут вероятности, с которыми тот или иной набор q D может реализоваться. В последнем случае информа-
ция, получаемая от эксперта, может быть, хотя бы частично, подкреплена статистическим анализом.
В этих случаях в качестве множества G можно выби-
рать множества |
в пространстве Еп, задаваемые условиями |
||
qi x,q 0 , i = |
1, 2, …, т, т.е. G q |
, |
q или P x G |
|
|
|
|
q D
, соответственно.
Последнее условие означает, что допускается нарушение ограничений (4.45), но вероятность такого нарушения не
должна превосходить некоторого критического значения . Теперь обратимся к критерию. Если критерий зависит от
неконтролируемых факторов, то выбор параметров x = (х1,
181
…, хп) не определяет однозначно величины Ф (х1, …, хп; q1,…, qk) и два разных проекта x и x могут при разных реализациях q и q оцениваться по-разному.
Избавиться от такой неопределенности можно разными путями. Можно, например, стать на позицию крайнего пессимизма и считать, что какой бы проект х мы ни выбрали, все неконтролируемые факторы будут нам неблагоприятствовать. В этом случае качество проекта оценивается величиной
Ôn x ,..., x |
n |
min Ô x ,..., x ;q ,...,q |
k |
. |
(4.47) |
|||
1 |
q D |
1 |
n |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
Можно, наоборот, считать, что условия полностью благоприятны, и оценка качества в этом случае будет оптимистической:
Ô0 x ,..., x |
max Ô x ,..., x ;q ,...,q |
k |
. |
(4.48) |
||||
1 |
n |
q D |
1 |
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
В действительности истинная оценка будет находиться где-то между величинами Фn и Ф0. Например, если неконтролируемые факторы подчинены некоторому распределению вероятностей, то в качестве оценки можно взять среднее значение – математическое ожидание
Ôñð x1,..., xn Ì |
Ô x1,..., xn ;q1,...,qk . |
(4.49) |
В приведенных выше способах избавления от неконтролируемых факторов в математической модели наиболее сложными являются преобразования системы ограничений.
Часто используется следующий прием, позволяющий перенести неопределенность из ограничений в критерий. В качестве множества допустимых значений конструктивных
параметров берется объединение G q ; т.е. рассматрива-
q D
ют все значения, которые допустимы хотя бы при одной реализации (q). Затем устанавливается штраф за нарушение
ограничения qi x,q 0 , он пропорционален величине qi x,q , если она оказалась положительной, т.е. штраф вида
182
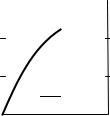
c |
ä |
x,q ,åñëè |
ä |
x,q 0, |
|
|
1 i |
|
i |
|
(4.50) |
i x,q |
|
|
0. |
||
0,åñëè äi x,q |
|
||||
|
|
|
|
|
|
Соотношение коэффициентов с1, с2, ..., сm отражает степень «важности» того или иного ограничения в системе (4.45).
Тогда критерием качества будет служить функция
Ô õ,q 1 x,q ... m x,q . |
(4.51) |
Рассмотрим теперь ситуацию, когда оценка качества проекта производится по нескольким показателям, т.е. имеется N критериев Ф1, ..., ФN.
Если для двух каких-то проектов x и x выполняются неравенства Ôk x Ôk x для всех k = 1, ..., N, то естест-
венно, что проект x предпочтительнее, чем x . Поэтому можно сразу ограничиться рассмотрением только таких величин х = (х1, ..., хп), что для любого другого набора значений
х' = (х'1, ..., х'п) из неравенства Ô k x Ô k x при некотором номере k следует, что при каком-то другом номере j справедливо Ô j x Ô j x . Такие решения называются
оптимальными по Парето. |
|
|
|
|
|
|
|
|
|
|
|
|
||
В |
качестве примера |
|
|
|
|
|
|
|
|
|
|
|
Кумулятивный |
|
приведем |
построение диа- |
100 |
|
|
|
|
|
|
|
|
|
|
процент |
|
|
|
|
|
|
|
|
|
|
|
100 |
||||
граммы Парето (рис. 4.2). |
80 |
|
|
|
|
|
|
|
|
|
|
80 |
||
На оси абсцисс отмечается |
|
|
|
|
|
|
|
|
|
|
||||
вид брака, на оси ординат – |
60 |
|
|
|
|
|
|
|
|
|
|
60 |
||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
число случаев брака в про- |
40 |
|
|
|
|
|
|
|
|
|
|
40 |
||
|
|
|
|
|
|
|
|
|
||||||
центах и числовом выра- |
20 |
|
|
1 |
2 |
3 |
|
4 5 |
|
|
20 |
|||
|
|
|
|
|
||||||||||
жении |
и |
вычерчивается |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
столбиковая диаграмма, за- |
Рис. 4.2. Диаграмма Парето по ви- |
|||||||||||||
тем – кумулятивная кривая. |
||||||||||||||
Брак материалов и разме- |
дам брака: 1 – брак материалов; 2 – |
|||||||||||||
ров составляет 70 %, а вме- |
брак в размерах; 3 – брак в форме; |
|||||||||||||
сте с браком формы это со- |
4 – брак в отделке; 5 – |
прочие ви- |
||||||||||||
ставит 90 % всего брака. |
|
|
|
|
|
ды брака |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
183 |
|
|
|
|
|
|
|
|
|
|
|
Оптимальные по Парето решения – это такие наборы значений конструктивных параметров, изменение которых не может привести к одновременному улучшению всех показателей (увеличению значений всех критериев). К сожалению, оптимальное по Парето решение, как правило, не единственно и возникает задача выбора одного из них. При этом если по каким-то показателям одно паретовское решение лучше другого, то непременно есть показатели, по которым первое решение хуже (иначе это другое решение не является паретовским).
Только лишь в рамках формальной математической модели вопрос о предпочтении того или иного оптимального по Парето решения разрешен быть не может. Многокритериальную задачу нужно свести к однокритериальной, т.е. система показателей Ф1, ..., ФN должна быть заменена одним критерием Ф. Такая замена называется сверткой критериев и может быть осуществлена многими различными способами. Рассмотрим некоторые из них, заметив предварительно, что замена Ф1, ..., ФN → Ф должна удовлетворять следующему свойству. Если для двух разных значений х и х' некоторые из показателей Ф1, ...,ФN не изменяются, а остальные улучшаются, т.е. соответствующие значения для х, например, больше, чем для х', то Ф(x) должно быть больше Ф(х'). Иначе говоря, если представить критерий Ф(x) в виде Ф (Ф1(x), ..., ФN (x)), то функция Ф (Ф1, ..., ФN) как функция N аргументов должна быть монотонно возрастающей по каждому аргументу.
1. Приписывая каждому показателю Фk «вес» λk, характеризующий его важность в системе показателей, получим такой критерий:
Ф (Ф1, ..., ФN) = 1Ô1 ... N Ô N . |
(4.52) |
2. Задавая некий минимальный уровень аk каждого критерия и ставя задачу как можно больше превзойти этот минимальный уровень по самому худшему показателю, получим еще один вид критерия:
184
Ô Ô1, ...,Ô N |
min Ô k ak , |
(4.53) |
k 1, ..., N. |
|
|
|
|
3. В следующем критерии, в основе которого лежат предыдущие, с помощью весов λk вводится предпочтение в системе показателей:
Ô Ô1,...,Ô N |
min k Ôk ak , k 1, ..., N . (4.54) |
4. Критерий Ф(Ф1, ..., ФN) = u1(Ф1) + ... + uN(ФN), где uk, k = 1, ..., N – монотонно возрастающие функции (обобщает
критерий 1) и дает возможность рассматривать нелинейные зависимости Ф от Фk. (Если, например, взять uk (Фk) = 1n Фk, то полученная свертка будет эквивалентна критерию Ф =
= (Ф1, Ф2, ..., ФN).
Можно привести и другие формы свертки критериев, все они призваны свести многокритериальную математическую модель к однокритериальной.
Следует отметить, что выбор свертки – задача не менее трудная, чем выбор искомого проекта среди паретовских – это всего лишь перенос неопределенности из пространства конструктивных параметров в пространство критериев. Как уже отмечалось, решение этой задачи не может быть эффективно осуществлено только математическими методами, но подразумевает активное участие специалиста в той области, к которой относится проектируемое изделие.
Фактически формирование свертки происходит в процессе отбраковки вариантов, если специалист владеет соответствующим механизмом отбраковки. Таким образом, происходит декомпозиция задачи многокритериальной оптимизации проекта. На ее первом этапе строится множество паретовских проектов – это вполне математическая задача, решение которой приводит к сужению пространства выбора конструктивных параметров. На втором этапе производится отбраковка вариантов на паретовском множестве с помощью некоторого специального механизма, позволяющего из двух паретовских решений выбрать один, предпочтительный по
185
некоторым соображениям. Эти соображения могут носить неформальный характер, но в благоприятном случае их удается выразить в форме стремления максимизировать некоторый функционал, заданный на паретовском множестве. В этом и заключается формирование свертки исходных критериев.
Таким образом, мы видим, что и при наличии неконтролируемых факторов, и в случае многих показателей качества можно построить модель простейшего типа, которая, по крайней мере, в первом приближении, будет служить описанием исследуемой задачи проектирования.
4.2. Идентификация
Оптимизация конструкций оборудования и технологических режимов является важнейшим направлением совершенствования промышленного производства. Эффективность решения этой проблемы требует применения математических методов, ориентированных на использование ЭВМ. Решающую роль в решении оптимизационных задач играет качест-
во математических моделей процесса. Повышение их адек-
ватности достигается с помощью различных методов идентификации при использовании результатов натурных опытов, поэтому цепочка эксперимент – модель – идентификация – оптимизация характеризуется наличием внутренних обратных связей, что приводит к необходимости ее целостного системного анализа.
Повышению уровню сходимости результатов расчета и эксперимента при усложнении и детализации математического описания реальных процессов препятствует внесение в модель неопределенностей в виде неточных коэффициентов, недостаточно обоснованных допущений в постановке задачи и т.д. Вопросы стыковки теории и эксперимента и изучает такая отрасль науки, как теория идентификации.
Цель идентификации – уменьшение расхождений между результатами испытаний изделия и расчета по модели без изменения ее структуры, а только за счет уточнения значений ряда параметров.
186
Можно выделить три основных направления в изучении технологических и физических процессов:
1)создание теоретических основ методов математического моделирования (ММ) и их реализация на ЭВМ;
2)развитие методик идентификации математических моделей;
3)чисто экспериментальное изучение процессов и яв-
лений.
Важнейшим вопросом повышения эффективности применения методов ММ и экспериментальных методов изучения сложных процессов является системное и согласованное использование теоретических и экспериментальных средств исследования процессов и методов идентификации. Разумного соотношения точности расчета и экспериментальных данных можно добиться путем организации опытных исследований и поиска моделей, удовлетворительно описывающих имеющиеся данные измерений.
Первое из направлений предполагает специальную организацию и планирование эксперимента, что существенно повышает эффективность анализа моделей и самого процесса.
Второе направление поисков разумного соотношения погрешностей моделирования и качества эксперимента связано с анализом качества расчетных моделей и выбором их оптимальной сложности.
Целью функционирования подсистемы идентификации является получение оптимальных значений параметров моделей и оценок точности этих значений. Можно выделить две основные проблемы идентификации:
1)оценивание параметров;
2)интерпретация полученных результатов.
Первая сводится к задаче математического программирования, т.е. к минимизации заданного критерия идентификации, вычисляемого на основе разности расчетных значений модели и экспериментальных данных.
Вторая задача идентификации – интерпретация полученных результатов. Оптимальные значения параметров модели, при которых обеспечивается наилучшее ее приближе-
187

ние к конкретным экспериментам, чаще всего не могут быть использованы в дальнейших расчетах без исследования их зависимости от параметров, взятых для оценивания данных. Такую информацию обычно получают с помощью методов математической статистики.
4.2.1. Методы идентификации
Рис. 4.3. Задача идентификации
Идентификацией называется оптимальная в некотором смысле модель (рис. 4.3), построенная по результатам наблюдений над входными и выходными переменными объекта.
Am f (U ,Y ) . |
(4.55) |
Задачи идентификации делятся на два типа:
1)структурные (или идентификация в широком смысле
слова);
2)параметрические (или идентификация в узком смысле
слова).
4.2.2. Структурная идентификация
Подразумевает построение модели типа «черный ящик», т.е. отсутствует априорная информация об объекте: неизвестна структура объекта, класс объекта, размерность и т.д. Главная задача структурной идентификации – определение структуры модели. Задача структурной идентификации в общем виде не решается.
Рекомендуется решать задачи структурной идентификации в следующей последовательности:
1. Определить тип (класс) моделей:
а) начинать построение модели с физической модели (по известным законам физики, не забывая о цели построения модели);
б) начинать с самых простых моделей (линейная, непрерывная, одномерная и т.д.);
188
в) постараться преобразовать модель к виду линейной регрессии:
yi a0 a1u1 ... anun . |
(4.56) |
2.Определить размер или порядок модели (определить количество внутренних переменных модели). Определить ковариационные (зависимость от шумовых характеристик)
икорреляционные (взаимосвязь между определенными двумя внутренними переменными) матрицы.
На сегодняшний день существует несколько методов исследования ковариационных и корреляционных матриц, которые позволяют определить недостаточность или избыточность модели.
3.Выполнить параметрическую идентификацию (способ параметризации модели).
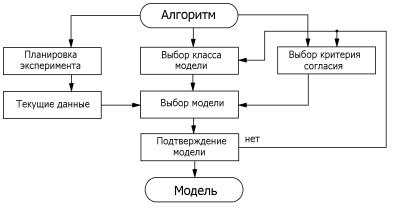
Рис. 4.4. Общая схема идентификации модели
Из рис. 4.4 видно, что основные составляющие задачи идентификации – это исходные (текущие) данные, выбор критерия согласия, выбор модели и метода идентификации. Рассмотрим каждую составляющую подробно.
189
4.2.2.1. Текущие данные
Текущие данные могут быть получены в результате пассивного или активного эксперимента. Пассивный эксперимент – когда исследователь не влияет на процедуру регистрации (изменения) данных. Активный эксперимент – когда исследователь формирует программу эксперимента.
Методами формирования эксперимента занимается специальная наука, называемая теорией планирования эксперимента. Основные подходы и планы экспериментов были рассмотрены выше. В результате активного эксперимента упрощается процедура идентификации.
4.2.2.2. Выбор класса модели
Тип модели задается в виде |
|
F (L, N, M , D) , |
(4.57) |
где L, N, M , D – булевые переменные, т.е. переменные, при-
нимающие значение либо 0 (нет), либо 1 (да); L характеризует объект как линейный, N – как непрерывный, M – как многомерный, D – как детерминированный.
Обычно идентификация начинается с расчета самой простой модели, а именно объект представляется в виде линейной, непрерывной, одномерной и детерминированной мо-
дели: |
|
F (1,1, 0,1). |
(4.58) |
4.2.2.3. Выбор критерия согласия
Модель объекта всегда неточна. Неточность модели по
отношению к объекту определяется функцией невязки: |
|
f ymi yi , |
(4.59) |
где ymi – значение i-й выходной переменной модели; |
yi – |
значение i-й выходной переменной объекта. |
|
190 |
|
