
Моделирование систем
..pdfx1 = 1, |
x2 = 0, x3 = 0, x4 = 0; |
||
y1 = –1, |
y2 = 2, |
y3 = 1, |
y4 = –1; |
z1 = 0, |
z2 = 1, |
z3 = 1, |
z4 = –1. |
После определения значений степеней при независимых параметрах выражения критериев подобия записываются в окончательном виде.
Для рассматриваемого примера окончательные выражения для критериев подобия в форме записи, соответствующей независимым переменным u, R, C, будут иметь вид
|
i |
; |
|
|
|
|
L |
|
; |
|
|
|
t |
|
; |
|
|
|
|
ω |
; |
|
|
|
uR 1 |
|
|
R2C |
|
|
|
|
|
|
R 1C 1 |
||||||||||||||
1 |
|
2 |
|
|
|
3 |
|
|
RC |
|
|
4 |
|
|
|
|
|
|||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
u |
|
|
2 2 |
|
1 |
|
|
L |
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
; |
|
3 |
|
|
; |
|
|
|
|
|
||||||||
|
|
iR |
|
Rt |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
RC |
|
4 3 4 ωt. |
|
|
|
|
|
|||||||||||||
|
3 3 |
|
|
|
t |
|
; |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
В примере возможна еще 21 форма записи (F = 22) кри- |
||||||||||||||||||||||||
териев подобия. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VI. Представляем |
|
описание |
|
исследуемого процесса |
||||||||||||||||||||
в виде критериального уравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Критериальное уравнение представляет собой описание |
||||||||||||||||||||||||
зависимого критерия. Для данного примера это 1 = = |
|
i |
||||||||||||||||||||||
|
|
. |
||||||||||||||||||||||
|
uR 1 |
|||||||||||||||||||||||
3.12. Применение третьей теоремы подобия для установления условий подобия
Третья теорема подобия (иначе называемая обратной теоремой подобия) определяет необходимые и достаточные условия для создания подобия. Наиболее распространена следующая ее формулировка: необходимыми и достаточными условиями для создания подобия систем являются про-
121
порциональность сходственных параметров, входящих в условия однозначности, и равенство критериев подобия сопоставляемых явлений. Третья теорема подобия именуется также обратной теоремой подобия или теоремой Кирпичева– Гухмана.
С п р а в к а. Дифференциальное уравнение в общем виде описывает бесконечное множество процессов, относящихся к данному классу. Условия, определяющие индивидуальные условия процесса или явления, называются условиями однозначности. К ним относятся следующие, не зависящие от механизма самого явления, факторы и условия:
1)геометрические свойства системы, в которой протекает процесс;
2)физические параметры среды и тел, образующих систему;
3)начальное состояние системы (начальные условия);
4)условия на границах системы (граничные или краевые условия);
5)взаимодействие объекта и внешней среды.
a |
|
|
d n x |
|
... a |
n 1 |
|
dx |
a |
n |
x 0, |
|
0 |
dt n |
dt |
||||||||||
|
|
|
|
|
(3.136) |
|||||||
|
|
|
k |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
x 0 x0. |
|||||
x t cê e Pêt , |
|
|||||||||||
i 1
Для дифференциальных уравнений любого порядка условия однозначности – начальные условия (задача Коши). Нельзя математически сформулировать условия однозначности в общем виде, для каждого конкретного случая они различны, зависят от рода решаемой задачи и от вида урав-
нения. Например, для уравнения u = iR + Ldidt , описывающего изменение тока в цепи с активным сопротивлением R
ииндуктивностью L при включении ее на u = const, достаточно задать параметры u, R, L и начальные условия i = i0
иt = t0.
122
В большинстве задач, связанных с исследованием полей, однозначность определяется не только начальными условиями, но и свойствами среды, геометрическими свойствами системы и граничными условиями.
3.13. Формулировка третьей теоремы, отвечающая реальным условиям задачи
Эта формулировка состоит из трех положений. Положение 1. Создание модели возможно, если крите-
рии подобия, составленные из величин, характеризующих только ее системные параметры, равны соответствующим критериям изучаемой системы-оригинала.
П р и м е ч а н и е. Частным случаем является равенство материальных параметров систем элементов модели и оригинала, выраженных в относительных единицах.
Положение 2. В созданной согласно положению 1 модели осуществление процессов, подобных оригиналу, возможно, если критерии подобия, содержащие только параметры процессов, входящих в условия однозначности и в том числе начальные условия (параметры исходного режима, возмущений и отклонений), в модели и оригинале соответственно одинаковы.
Пр и м е ч а н и е. Частным случаем является равенство параметров исходного режима в модели и оригинале, выраженных в относительных единицах.
Положение 3. Создание модели согласно положениям 1
и2 возможно в сколь угодно сложных анизотропных (изотропные системы имеют одинаковые физические свойства – электропроводность, теплопроводность, упругость и т.п. – по всем направлениям внутри системы; анизотропные системы имеют различные свойства по разным направлениям), нелинейных или имеющих вероятностно заданные параметры системах при условии одновременного соблюдения соответствующих дополнительных положений.
Пр и м е ч а н и я:
1. Третья теорема в формулировке положения 1 имеет ряд ограничивающих условий. В частности не распространя-
123
ется на автомодельные системы, для которых нельзя составить ни одного критерия, содержащего только параметры системы, но можно при любых их значениях осуществлять переход от характеристик одного процесса к характеристикам другого за счет изменения только масштабов параметров процесса.
2. В указанных выше положениях понимается, что система представляет собой совокупность взаимодействующих элементов, связанных в той или иной мере единством происходящих процессов.
Этих положений достаточно, чтобы пользоваться третьей теоремой, не заботясь о ее доказательствах.
3.14. Автомодельность
При постановке и обработке опытов важно учитывать, что в различных отраслях техники встречаются явления (процессы), которые называются автомодельными.
Автомодельность какого-либо явления означает автоматическое сохранение его подобия исходному явлению (оригиналу) независимо от абсолютных значений параметров элементов той системы, в которой данное явление происходит.
Формальный признак автомодельности – выполнение условия:
mэ.с k, |
(3.137) |
где mэ.с – число параметров элементов системы.
Процессы, описываемые двучленными уравнениями, всегда автомодельны. Критерии подобия автомодельных процессов при моделировании служат не для расчета значений параметров элементов модели, а лишь для определения масштабов при любых значениях параметров элементов модели.
Признак автомодельности: из формулировки третьей теоремы подобия следует, что процессы, протекающие в системах, из параметров которых нельзя составить ни одного безразмерного комплекса, являются автомодельными. При этом в представленные в критериальной форме дифференци-
124

альные уравнения и начальные условия войдут только выраженные в относительных единицах параметры, и процессы будут подобными при любых значениях параметров системы.
Рассмотрим понятие автомодельности на примере уравнения второго закона Ньютона:
f = |
Md 2l |
. |
(3.138) |
|
dt 2 |
||||
|
|
|
Уравнение содержит четыре параметра (f, M, l, t), т.е. n = 4. Для описания размерности параметров достаточно l = 3 основных единиц системы СИ:
f L1M 1T 2M L0M 1T 0l L1M 0T 0t L0M 0T1
Матрица размерностей:
1 1 2
0 1 0
1 0 0
0 0 1
(3.139)
(3.140)
Общее число определителей третьего порядка:
C43 |
4! |
|
4 . |
(3.141) |
|
3!(4 3)! |
|||||
|
|
|
|||
Все определители отличны от нуля, так ни один из них не содержит строку, являющуюся линейной комбинацией двух остальных. Следовательно, любые три из четырех параметров могут быть выбраны в качестве независимых (в том числе f и M), т.е. процессы, описываемые уравнением второго закона Ньютона, подобны при любых значениях f и M и, следовательно, автомодельны.
125
Пример. Рассмотрим процессы в электрической цепи, представляющей собой включение R1 L1 на постоянное напряжение u1. Уравнение описываемого процесса имеют вид
u |
|
i R |
L di1 . |
(3.141) |
|
1 |
1 1 |
1 dt1 |
|
Критерии подобия процесса имеют вид (один из возможных)
1 |
i1 R1 |
; |
2 |
|
t1 R1 |
. |
(3.142) |
|
|
||||||
|
u1 |
|
|
L1 |
|
||
При этом только один критерий независимый. Для обеспечения подобия второго процесса (в аналогичной электрической цепи, но с другими параметрами) первому (исходному) необходимо, чтобы определяющие критерии в сходственные моменты времени были равны, т.е. чтобы
2 2 |
|
t1 R1 |
|
t2 R2 |
. |
(3.143) |
L1 |
|
|||||
|
|
|
L2 |
|
||
При любых заданных значениях L2 и R2 всегда можно удовлетворить этим условиям соответствующим выбором величины t2 и, следовательно:
mt = t1 / t2. |
(3.144) |
Если R1/L1 R2/L2 или mR/mL 1, то и mt = mR/mL 1. Таким образом, при соответствующем выборе масштаба
времени рассматриваемые два процесса будут подобны при любых значениях параметров элементов второй системы (R2, L2). Значение еще одного параметра второй системы u2 никакого влияния на подобие процессов не оказывает, поскольку он входит в неопределяющий критерий. Следовательно, величина u2 может быть любой, что также соответствует и тому, что u2 входит в систему независимых параметров второго процесса.
126

Итак, при любых значениях параметров элементов системы (u, R, L) процессы в цепях RL оказываются подобными. Следовательно, эти процессы можно считать автомодельными. При этом необходимо учитывать ограничения, наложенные на выбор масштаба времени mt.
Процессы, протекающие в цепях RLC, не могут быть полностью автомодельными, поскольку число независимых параметров меньше числа параметров системы.
Заключительный пример к теоремам подобия. Диф-
ференциальное уравнение переходного процесса в цепи из активного сопротивления R, индуктивности L и емкости C при включении на источник постоянного напряжения u
u L dtdi C1 idt Ri.
Для конкретного процесса следует задать значения параметров u, R, L, C и начальные условия i = 0 при t = 0. При
этом по -теореме из шести параметров (m = 6) три являются независимыми (k = 3), и, следовательно, число критериев подобия составляет m – k = 3, причем существует 15 форм записи трех критериев. Если независимые переменные – это u, C и t, получаются следующие критерии:
|
it |
; |
|
|
|
RC |
; |
|
|
|
LC . |
uC |
|
t |
|
||||||||
1 |
|
|
2 |
|
|
|
3 |
|
t2 |
Пусть существуют два процесса, у которых критерии 2 и 3 равны. Покажем, что равенства этих критериев доста-
точно для подобия процессов. Если критерии 2 и 3 соответственно одинаковые у двух процессов, то
|
|
|
|
|
|
|
R1C1 |
|
R2C2 |
; |
L1C1 |
|
|
|
L2C2 |
|
||||||
|
|
|
|
|
|
|
|
t1 |
|
t12 |
|
t22 |
||||||||||
или |
|
|
|
|
|
|
t2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
R1 |
|
|
C1 |
|
|
|
|
|
|
L1 |
|
|
C1 |
|
|
||||||
|
R2 |
|
|
C2 |
mRmC |
1; |
|
L2 |
C2 |
mL mC 1. |
||||||||||||
|
|
t1 |
|
|
||||||||||||||||||
|
|
|
|
m |
|
|
|
|
2 |
m2 |
||||||||||||
|
|
|
|
|
|
t |
|
|
|
|
t1 |
|
|
|
t |
|||||||
|
|
t2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t2 |
|
|
|
|
||||
127

Поскольку u, C и t – независимые параметры, то и масштабы можно выбрать произвольно. Отсюда масштабы сопротивлений и индуктивностей:
mR mt ; mC
m2 mL mt .
C
Если произвольно выбраны mu, mC и mt и определены mR и mL, то при 2 = 3 масштаб токов mi будет таким, что всегда справедливо условие
mi mt 1 . mu mC
Параметры первого процесса: u1 = 500 В, R1 = 30 Ом,
L1 = 2,62 Гн, C1 = 2 10–3 Ф. Зададимся mu = 5; mC = 0.4; mt = 1.
Тогда
mR = mL = 0,14 = 2,5,
параметры второго процесса: u2 = u1/mu = 500/5 = 100 В;
R2 = R1/mR = 30/2,5 = 12 Ом; L2 = L1/mL = 2,62/2,5 = 1,045 Гн; C2 = C1/mC = 2 10–3/0,4 = 5 10–3 Ф.
При данных параметрах для сходственных моментов времени критерии 2 и 3 соответственно одинаковы для обоих процессов. Например, при t1 = t2 = 0,125 c
2 |
= |
30 2 10 3 |
|
12 5 10 |
3 |
|
|
|
|
0,125 |
|
0,125 |
0,480; |
|
|||||
|
|
|
|
|
|
|
|
||
3 = |
2 62 2 10 3 |
|
1,045 5 10 3 |
|
0 |
. |
|||
|
0,1252 |
0,1252 |
336 |
||||||
|
|
|
|
|
|
||||
Для обоих процессов R2C – 4L < 0 и, следовательно, решение исходного уравнения имеет вид
128

u exp |
|
4 L R |
2 |
C |
2 |
|
Rt / 2L sin t |
|
4L C |
||||
i |
|
|
|
|
|
. |
L4L R 2C  4L2C
4L2C
Втабл. 3.4 приведены результаты расчета значений то-
ков i1 и i2. Соответствующие зависимости i = f (t) представлены на рис. 3.8.
|
|
|
|
|
|
Таблица 3.4 |
|
|
Результаты расчета значений токов i1 и i2 |
||||||
|
|
|
|
|
|
|
|
t, c |
i1 |
|
i2 |
t, c |
i1 |
|
i2 |
|
A |
|
A |
||||
|
|
|
|
||||
0,000 |
0,000 |
|
0,000 |
0,500 |
0,000 |
|
0,000 |
0,125 |
7,450 |
|
3,725 |
0,625 |
0,430 |
|
0,215 |
0,250 |
0,000 |
|
0,000 |
0,750 |
0,000 |
|
0,000 |
0,375 |
–1,820 |
|
–0,910 |
0,875 |
–0,093 |
|
–0,047 |
Рис. 3.8. Зависимость i= f(t)
129
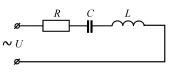
Видно, что для сходственных моментов времени отношения токов постоянно: mi = 2.
При этом |
mi mt |
|
2 1 |
1. |
|
|
|||
|
mu mC |
5 0,4 |
|
|
Таким образом, равенство критериев подобия 2 и 3 оказывается достаточным для того, чтобы выполнялись условия, накладываемые на масштабы. Поскольку пропорциональность всех параметров существует и эти условия соблюдены, то рассматриваемые процессы подобны.
3.15. Масштабные уравнения
Рассмотрим составление масштабных уравнений на примере.
На рис. 3.9 представлен контур с цепью R-L-С. Данный электрический контур описывается уравнением
L |
d 2i |
|
1 |
i R |
di |
U sin ωt . |
(3.145) |
|
dt2 |
C |
dt |
||||||
|
|
|
|
|
Рис. 3.9. Электрическая цепь
R-L-С
Рассмотрим два процесса с параметрами:
{L1, R1, С1, t1, i1, U1, 1} = P1,
{L2, R2, С2, t2, i2, U2, 2} = P2.
По каждому из параметров введены определенные масштабные коэффициенты:
m |
L |
|
L2 |
, m |
R |
|
R2 |
, m C2 |
, m |
t |
t2 |
, |
||||
|
|
|||||||||||||||
|
|
L1 |
|
|
R1 |
|
C |
C1 |
|
|
|
t1 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
m |
i2 |
, m U 2 |
, m |
|
ω2 . |
|
(3.146) |
||||||
|
|
|
i |
i |
|
|
U |
U |
1 |
ω |
|
ω |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
Воспользуемся ранее выведенными критериями, но по принципу размерности:
130
